Контрольные вопросы

1. Что такое независимые начальные условия?

2. Как определяется постоянная времени последовательной RL-цепи? Объясните физический смысл этой величины.

3. Опишите характер переходного процесса в последовательной RL-цепи при ее подключении к источнику гармонической ЭДС,

4. Как зависит характер переходных процессов от соотношения между начальной фазой источника ЭДС и аргументом комплексного входного сопротивления цепи.

5. При каких условиях переходный процесс в последовательной RL-цепи с гармони­ческим источником не происходит? Почему?

Лабораторная работа № 5

ИССЛЕДОВАНИЕ ПАССИВНЫХ ДИФФЕРЕНЦИРУЮЩИХ

И ИНТЕГРИРУЮЩИХ ЦЕПЕЙ

Цель работы: изучить прохождение сигналов через пассивные дифференцирующие и интегрирующие цепи.

Краткие теоретические сведения

Дифференцирующей цепью называется четырехполюсник, напряжение на вы­ходе которого пропорционально производной по времени от напряжения на входе:

В качестве дифференцирующего элемента можно использовать конденсатор или ка­тушку индуктивности, т.к. для этих элементов ток и напряжение связаны операциями дифференцирования и интегрирования:

.

Е сли дифференцирующая цепь выполняется на конденсаторе, то входным сигналом должно быть напряжение, приложенное к конденсатору, а выходным сиг­налом - напряжение, пропорциональное току через конденсатор. Практически для получения выходного напряжения, пропорционального току, можно последовательно с конденсатором включить резистор, и выходное напряжение снимать с него (рис. 5.1. а).

Если дифференцирующая цепь выполняется на индуктивности, то входное напряжение должно быть преобразовано в пропорциональный этому напряжению ток через катушку, тогда выходным сигналом будет напряжение на катушке. Для за­дания тока, пропорционального входному напряжению, можно последовательно с катушкой включить резистор с большим сопротивлением; выходное напряжение, очевидно, следует снимать с индуктивности (рис. 5.1, б). В принципе, сравнивая рис. 5.1,а и 5.1, б, можно еще раз убедиться в дуальности индуктивного и емко­стного элементов. Действительно, обе схемы однотипны, только заменены тип реак­тивного элемента и его местоположение относительно активного сопротивления. Практически, дифференцирующие цепи на индуктивностях почти не применяют, так как изготовление катушек нетехнологично, катушки имеют большие габариты и мас­су, высокую стоимость, кроме того, они чувствительны к паразитным внешним на­водкам. Конденсаторы же, напротив, являются технологичными: промышленностью выпускаются конденсаторы в широких диапазонах емкостей и рабочих напряжений. Конденсаторы существенно меньше, чем катушки; подвержены паразитным внеш­ним наводкам; они, как правило, имеют меньшие, чем катушки, габариты, массу и стоимость. С учетом сказанного, далее будем рассматривать RC дифференцирую­щие цепи (рис. 5.1, а).

Наличие резистора в цепи приводит к тому, что к конденсатору прикладывает­ся не все входное напряжение, а его часть, равная разности входного напряжения и напряжению на резисторе; следовательно, выходной сигнал становится пропорцио­нальным производной не самого входного сигналами его части: возникает ошибка. Точность дифференцирования, очевидно, будет тем меньше, чем больше падение напряжения на резисторе (выходное напряжение), а оно, в свою очередь, возрастает с величиной сопротивления.

Другими словами, рассматриваемая цепь сохраняет дифференцирующие свойства при выполнении условия ; в этом случае .

С учетом этого, можно записать:

,

где – постоянная времени цепи.

По мере увеличения сопротивления R форма выходного напряжения все больше отличается от формы производной входного напряжения и приближается к форме самого входного напряжения; при цепь из дифференцирующей превращается в разделительную. Таким образом, цепь можно считать дифференци­рующей при выполнении следующих равноценных условий:

; ,

где ω – частота входного сигнала. Предельной частотой входного сигнала, при кото­рой цепь еще можно приближенно считать дифференцирующей, считают граничную частоту

.

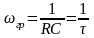В последних выражениях подразумевалось, что сигнал является гармониче­ским, практически же сигнал может быть любым. Для периодического негармониче­ского сигнала, и тем более, для непериодического сигнала удобнее пользоваться для оценки дифференцирующих свойств цепи не величиной частоты, а величиной периода (для периодического сигнала) или длительности (для непериодического сигнала, например, для импульса). Для того чтобы цепь была дифференцирующей, необходимо выполнение условия: ,

где Т – период или длительность входного сигнала.

Выше было показано, что при дифференцировании выходной сигнал должен быть много меньше входного сигнала, однако при дифференцировании импульсов с крутыми фронтами очевидно должны получаться короткие импульсы большой ам­плитуды (производной ступенчатой функции является δ - функция).

Таким образом, пассивная дифференцирующая цепь обладает рядом недос­татков: дифференцирование осуществляется приближенно, выходной сигнал дол­жен быть много меньшим, чем входной (коэффициент передачи пассивной диффе­ренцирующей цепи много меньше единицы). Для устранения этих недостатков на практике широко применяют активные дифференцирующие цепи, которые выполня­ют, как правило, на операционных усилителях – специальных интегральных усили­телях с большим коэффициентом усиления и дифференциальным входом; в качест­ве дифференцирующего элемента в таких схемах, как и в пассивных схемах, приме­няют конденсатор. Подробное рассмотрение процессов в активной дифференци­рующей цепи выходит за рамки настоящей работы.

Несмотря на имеющиеся недостатки, пассивные дифференцирующие цепи часто используются на практике. Особенно широко такие цепи применяют для фор­мирования коротких импульсов с крутыми фронтами в импульсных и цифровых уст­ройствах, в устройствах автоматики и в Других устройствах радиоэлектроники. Ак­тивные дифференцирующие цепи могут применяться и для вычисления производной какого-либо сигнала (функции) в аналоговых вычислителях (пассивные цепи для этой цели непригодны из-за низкой точности).

Интегрирующей цепью называется четырехполюсник, напряжение на выходе которого пропорционально интегралу от напряжения на входе:

~ .

Как и дифференцирующие цепи, интегрирующие цепи могут быть активными и пассивными. В качестве интегрирующего элемента также можно использовать кон­денсатор или катушку индуктивности. Учитывая, что интегрирование - это обратная дифференцированию операция, можно воспользоваться рассуждениями, приведен­ными выше для дифференцирующих цепей, поменяв только местами входной и вы­ходной сигналы на конденсаторе или катушке.

Действительно, для конденсатора и катушки можно написать:

;

.

Если интегрирующая цепь выполняется на конденсаторе, то входное напря­жение должно быть преобразовано в пропорциональный этому напряжению ток че­рез конденсатор, тогда выходным сигналом будет напряжение на конденсаторе. Для задания тока, пропорционального входному напряжению, можно последовательно с конденсатором включить резистор; выходное н апряжение, очевидно, следует сни­мать с конденсатора (рис. 5.2, а).

Если интегрирующая цепь выполняется на индуктивности, то входным сигна­лом должно быть напряжение, приложенное к катушке, а выходным сигналом - на­пряжение, пропорциональное току через катушку. Для получения выходного напря­жения, пропорционального току, можно последовательно с катушкой включить рези­стор, и выходное напряжение снимать с него (рис. 5.2, б). Практически, интегри­рующие цепи на индуктивностях почти не применяют по тем же причинам, из-за ко­торых не применяют дифференцирующие цепи на индуктивностях (см. выше). Далее будем рассматривать RC интегрирующие цепи (рис. 5.2, а).

Рассматриваемая цепь сохраняет интегрирующие свойства при выполнении условия: , в этом случае

.

С учетом этого, можно записать:

,

где - постоянная времени цепи.

Можно также записать условие, при котором цепь сохраняет интегрирующие свойства, в виде:

,

где ω - частота входного сигнала. Минимальной частотой входного сигнала, при ко­торой цепь уже можно приближенно считать интегрирующей, считают граничную частоту:

.

Если же , то падением напряжения на сопротивлении R можно пренебречь и считать . Интегрирование в такой цепи не осуществляется.

Очевидно, пассивная интегрирующая цепь обладает теми же недостатками, что и пассивная дифференцирующая цепь: интегрирование осуществляется при­ближенно, выходной сигнал должен быть много меньшим, чем входной (коэффици­ент передачи пассивной интегрирующей цепи много меньше единицы). Для устране­ния этих недостатков применяют активные интегрирующие цепи на операционных усилителях с конденсатором в цепи обратной связи. Подробное рассмотрение ак­тивных интегрирующих цепей выходит за рамки настоящей работы.

Пассивные интегрирующие цепи часто используются на практике для получе­ния выходных сигналов, длительность которых больше, чем у входных сигналов, а крутизна фронтов - меньше. Такие цепи могут применяться для расширения им­пульсов в импульсных и цифровых схемах, для подавления импульсных помех при передаче разнообразных сигналов, для преобразования длительности импульсов в амплитуду и для других целей. Активные интегрирующие цепи могут применяться и для вычисления интеграла какого-либо сигнала (функции) в аналоговых вычислите­лях (пассивные цепи для этой цели непригодны из-за низкой точности)

Поскольку реально любая цепь всегда нагружена на какое-то сопротивление, это необходимо учитывать при рассмотрении дифференцирующих и интегрирующих цепей.