Контрольные вопросы

1. Что такое переходный процесс?

2. Объясните порядок расчета переходного процесса.

1. Что такое постоянная времени цепи? Как она определяется для последователь­ной RC-цепи? Объясните физический смысл этой величины.

2. Опишите характер переходного процесса а последовательной RC-цепи при скач­кообразном изменении ЭДС.

3. Как будет выглядеть график переходного процесса в последовательной RC-цепи при скачкообразном изменении ЭДС от большего значения к меньшему?

4. Почему для практических целей можно считать, что переходный процесс заканчивается через интервал времени (3...5)τ?

Лабораторная работа № 4 исследование переходных процессов в последовательной rl-цепи при подключении ее к источнику гармонического напряжения

Цель работы: изучить характер переходных процессов, происходящих в последова­тельной RL-цепи при ее подключении к источнику гармонического напряжения.

Краткие теоретические сведения

Р ассмотрим цепь, изображенную на рис. 4.1.

В момент времени t = 0 замыкают ключ S. Поскольку до коммутации цепь бы­ла разомкнута, ток в контуре был равен ну­лю. С уметом этого, источник ЭДС описыва­ется выражением:

Дифференциальное уравнение цепи, составленное относительно тока

i = i_L, при t ≥ 0 имеет вид:

.

Решение будем искать в виде суммы принужденной и свободной составляю­щих:

i = i_пр + i_св.

Принужденная составляющая может быть найдена методом комплексных ам­плитуд:

,

где ; – модуль и аргумент комплексного входного сопротивления цепи.

Характеристическое уравнение цепи имеет вид:

Lp + R = 0.

Уравнение имеет один корень:

,

где величина τ = L/R, имеющая размерность времени, называется постоянной времени последовательной RL-цепи.

Свободная составляющая тока i_св содержит один экспоненциальный член:

.

Подставляя найденное значение i_св в выражение для i и учитывая независи­мое начальное условие i (0) = 0, найдем постоянную интегрирования A₁:

.

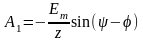Подставляя найденное значение A₁ в выражение для полного тока i, получим:

.

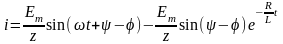Для напряжения на резисторе выражение имеет вид:

.

Из полученных выражений видно, что характер переходных процессов суще­ственно зависит от соотношения между начальной фазой ψ ЭДС источника напря­жения и аргументом φ входного сопротивления цепи. Если ψ - φ, то свободная со­ставляющая тождественно равна нулю. Переходные процессы в этом случае отсут­ствуют, т. е. установившийся режим наступает сразу же после коммутации. Если (k - нечетные числа), то начальные значения свободной и принужденной составляющих максимальны, поэтому отличия в форме кривых полных и принуж­денных составляющих токов и напряжений выражены наиболее резко. Максимально ток или напряжение может увеличиться в два раза (это возможно при очень боль­шом значении ).

Порядок выполнения работы

1.Аналитически рассчитать зависимость напряжения на резисторе от времени u_R(t); расчет провести, используя классический метод анализа переходных про­цессов.

2. Собрать в программе Electronics Workbench установку, показанную на рис. 4.2

3. Задать в программе режим анализа переходных процессов (параметр «Transient» в меню «Circuit - Analysis options») и покадровый режим работы осциллографа (флажок «Pause after each screen» в меню «Circuil -Analysis options»).

4. Установить на осциллографе время развертки таким образом, чтобы горизон­тальный размер экрана примерно соответствовал времени 5τ, для этого следует выбрать время развертки time base ≈ 5τ/14; т.к. время развертки не может быть установлено произвольно, то полученное значение следует округлить до бли­жайшего имеющегося значения, округлять предпочтительнее в большую сторону.

Рис. 2.3.2

2. Усиление соответствующего канала на осциллографе необходимо установить так, чтобы осциллограмма процесса полностью умещалась на экране. Осцилло­граф следует переключить в режим открытого входа (DC).

3. Установить начальную фазу источника ЭДС равной найденному в п. 1 аргументу комплексного входного сопротивление цепи. Следует учесть, что в программе начальная фаза задается в градусах, а в формулах часто применяют радианную меру.

4. Включить схему. Зарисовать полученную осциллограмму (с указанием времени развертки и усиления используемого канала осциллографа).

5. Повторить действия п. 6 для следующих значений начальной фазы источника ЭДС: ψ = φ + 45°; ψ = φ + 90⁰; ψ = φ + 135°; ψ = φ + 180°_; φ = φ + 225°; ψ = φ + 270°; ψ = φ + 305°.

6. Изменяя параметры схемы (амплитуду, частоту и начальную фазу ЭДС, индук­тивность катушки, сопротивление резистора), посмотреть их влияние на переход­ный процесс. При необходимости следует изменить время развертки и усиление(п. 4). После каждого изменения параметров схемы или режимов осциллографа следует выполнять действия п. 6. При проведении экспериментов следует также учитывать соотношение между постоянной времени цепи и периодом колебаний источника ЭДС. Исходные параметры схемы специально подобраны таким образом, чтобы переходный процесс длился по времени в течение нескольких перио­дов колебаний принужденной составляющей, это сделано для удобства наблю­дений.

7. Заполнить отчет. Отчет должен содержать титульный лист, цель работы, схему исследуемой цепи, осциллограммы процесса при различных значениях началь­ной фазы источника ЭДС (п.п. 5 - 7), выводы.