Порядок выполнения работы.

1 . Собрать электрическую цепь по схеме рис. 2.3, а для полосового или 2.3, б для заградительного фильтра по заданию преподавателя.

Рис. 2.3, а.

Рис. 2.3, б.

2. Рассчитать резонансную частоту фильтра.

3. Установить частоту генератора 1000 Гц и напряжение амплитудой 10 В.

4. Регулятором частоты установить резонансную частоту и измерить напряжения на входе и выходе фильтра. Результаты занести в таблицу 2.1.

5. По осциллограмме определить коэффициент фазы β. Для этого на экране осциллографа для полученной фигуры необходимо измерить расстояния М и Н в делениях шкалы экрана (рис.2.4) и рассчитать β = arcsin(M/H). Если на экране осциллографа получен круг или эллипс с одной вертикальной осью, а другой горизонтальной, то угол β= ±π/2, если прямая, то β = 0.

6. Регулятором частоты звукового генератора установить три значения частот до резонанса, измерить для них выходные напряжения фильтра и определить β.

Таблица 2.1

№	f	U1	U2	kU	M	H	β	примечание
	Гц	В	В		дел.	дел.	град.
1.								ω < ωp
2.
3.
4.								ω = ωp
5.								ω > ωp
6.
7.

7. Регулятором частоты установить три значения частоты после резонанса, измерить для них входные и выходные напряжения фильтра, и коэффициенты фазы.

8. По измеренным значениям напряжений вычислить значения коэффициента передачи k_U.

9. По формулам 2.4 или 2.5 в соответствии с типом фильтра рассчитать передаточную функцию для заданных значений сопротивления, индуктивности и емкости для трех частот (до резонанса, резонанс, после резонанса) и сравнить с полученными в п.10.

10. По данным таблицы 2.1 построить зависимости k_U(f), β(f).

Рис. 2.4.

Контрольные вопросы.

1. Что называется частотным электрическим фильтром?

2. Какие фильтры называются k-фильтрами, m-фильтрами?

3. Какие фильтры называются полосовыми?

4. Какие фильтры называются заградительными?

5. Что называется полосой пропускания фильтра?

6. Определите полосу пропускания исследуемого вами фильтра по графику зависимости k_U(f).

7. Объясните принцип работы исследуемого фильтра.

Лабораторная работа №3

ИССЛЕДОВАНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ

В ПОСЛЕДОВАТЕЛЬНОЙ RC-ЦЕПИ ПРИ СКАЧКООБРАЗНОМ

ИЗМЕНЕНИИ ЭДС.

Цель работы: изучить характер переходных процессов, происходящих в последова­тельной RC-цепи при скачкообразном изменении ЭДС; сравнить результаты экспе­римента и аналитического расчета.

Краткие теоретические сведения

Рассмотрим цепь, изображенную на рис. 3.1.

В момент времени t=0 ключ S переключают из положения 1 в положение 2. До коммутации цепь находилась в установившемся режиме. Для удобства анализа при­ведем схему к следующему виду (рис. 3.2).

Здесь источник ЭДС описывается выражением:

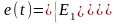
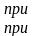
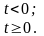
Составим дифференциальное уравнение цепи относительно напряжения на конденсаторе u_c:

.

Решение будем искать в виде суммы принужденной и свободной составляю­щих:

.

Принужденная составляющая определяется конечным установившимся со­стоянием цепи, в нашем случае:

.

Характеристическое уравнение цепи имеет вид:

.

Уравнение имеет один корень:

,

где величина 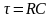, имеющая размерность времени, называется постоянной времени последовательной RC-цепи.

Свободная составляющая напряжения на емкости содержит один экспоненци­альный член:

.

Подставляя найденное значение u_{C св} в выражение для u_C и учитывая независимое начальное условие u_C(0)=E₁, найдем постоянную интегрирования A₁:

A₁ = E₁ – E_2.

Окончательно имеем:

;

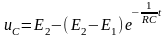или, с учетом введенного обозначения:

Из полученного выражения видно, что постоянная времени цепи - это величи­на, численно равная промежутку времени, в течение которого свободные состав­ляющие тока и напряжения уменьшаются в e ≈ 2,718 раза. Теоретически переходный процесс длится бесконечно долго, однако для практических целей считают, что про­цесс установления нового режима цепи (переходный процесс) заканчивается через промежуток времени (3...5)τ после коммутации.