1) Методика интерпритации аномалий магнитного поля Выполнить геологическую интерпретацию данных магнитной съемки какого-либо участка – означает выявить такие особенности его геологического строения, которыми объясняется картина наблюденного магнитного поля.

Интерпретация является наиболее сложным и ответственным этапом магниторазведочных работ.

При интерпретации результатов магниторазведки очень важно установить геологическую природу отдельных аномалий или аномальных зон и попытаться выяснить, какие геологические процессы привели к образованию объектов, обладающих аномальной намагниченностью по отношению к вмещающим породам. Поэтому, приступая к интерпретации, необходимо, чтобы был собран весь возможный материал о геологическом строении участка, магнитных и плотностных свойствах пород, участвующих в его строении.

качественную интерпретацию: дают описание структуры поля, выделяют отдельные области с однотипным полем, например, нормальным, спокойным, повышенным или пониженным или резко возмущенным и т.п. Характеризуют отдельные аномалии – указывают их: интенсивность, форму, размеры, простирание и на базе опыта проведения работ в подобных районах делают предположительное заключение о природе аномалий, т.е. о происхождении и составе пород, слагающих возмущающие объекты. Выделяют региональные и локальные аномалии.

Региональными называются аномалии, проявляющиеся на больших площадях (в десятки и сотни тысяч кв.км) и обусловленные крупными образованиями в земной коре и верхней мантии. Присутствие региональных аномалий обычно проявляется в тенденции изолиний поля к ориентировке (вытягиванию) в определенном направлении и в систематическом изменении величин, характеризующих поля в этом направлении. Перпендикулярно к этому направлению поля обычно плавно изменяются.

Локальные аномалии проявляются на картах в трех формах:

1) наличием систем замкнутых изолиний с одним или несколькими относительными максимумами или минимумами;

2) наличием локальных вариаций (изгибов) в ходе изолиний;

3) наличием сгущений изолиний (зон резко повышенного градиента поля). По своей морфологии локальные аномалии обычно подразделяются на изометричные и линейные. Изометричные аномалии характеризуются концентрическим характером изолиний, линейные – параллельным расположением с резким изменением формы в области замыкания.

Под количественной интерпретацией понимается нахождение по наблюденному аномальному полю параметров распределения масс (элементов залегания возмущающих тел) на основе аналитических или графических соотношений. Количественная интерпретация может включать в себя определение всех или только некоторых параметров возмущающих тел. Методы количественной интерпретации аномалий опираются на теорию решения прямой и обратной задач гравитационно-магнитного потенциала.

2.Решение прямой и обратной задачи для тонкого вертикального стержня.

У тонкого вертикального стержня, при однородной и вертикальной намагниченности, магнитные заряды будут располагаются только на его концах, внутри тела зарядов не будет, поскольку намагниченность допускаем однородной. На боковой поверхности их также не будет, т.к проекция J на внешнюю нормаль поверхности будет равно нулю.

В простейшем случае принимают, что длина стержня велика и нижний конец располагается на большой глубине и его влиянием на местную аномалию можно пренебречь. Следовательно длинный ТВС является эквивалентным точечному заряду или магнитному полюсу.

Модуль вектора напряжённости поля такого источника в любой точке может определить по закону Кулона:

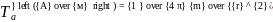
По может быть найдено значение модуля вектора магнитной индукции, выраженное в нанотесла:

Изменение 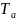по профилю, проходящему через эпицентр стержня, будет определятся уравнением:

В прямоугольной системе координат:

Особенности кривых z и H:

Кривая Z_а всюду положительна, имеет max над телом, т.е. при x=0 ( )

Расстояние от max до полу-max ( ) имеет величину , т.е. зная мы можем определить глубину залегания. H_а в левой части положительна, в правой – отрицательна, над телом (при x=0) превращается в 0. Max H_а наблюдается при x_э=-0.7h. Векторы T_а во всех точках будут направлены на полюс.

При решении обр. задачи, т.е. определении параметров тела по аномалии можно и нужно находить глубину залегания полюса

или , где

Определить намагниченность и диаметр стержня нельзя

3)Теорема Пуассона. Полученную связь называют уравнением Пуассона. Ее можно записать в сокращенном виде

U=-J_x

Уравнение Пуассона позволяет вычислять магнитный потенциал и его производные по известному гравитационному потенциалу и его производным.

В магниторазведке наряду с основной характеристикой поля- вектором магнитной индукции, используют вспомогательную характеристику-вектор напряженности поля. В связи с этим имеет смысл ввести следующие обозначения. Модуль и составляющие вектора магнитной индукции обозначить через Т,Х,Y,H,Z, а соответствующие элементы вектора напряженности через T^*, X^*,Y^* ,H^*,Z^*.

Дифференцированием получают уравнение связи между составляющими вектора и элементами векторов градиентов поля силы тяжести

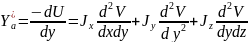
К составляющим вектора переходят по формулам

При вычислениях правые части всех равенств умножают на коэффициент 1/4πσ.

В частном случае при вертикальной намагниченности и

U_a =-J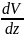 тогда

; ;

4.Решение прямой и обратной задачи для шара или вертикального диполя.

В природе нет геол. Тел имеющих форму шара. Однако знать хар-ку аномалии от шара важно, т.к. аномалии от реальных тел неправильной формы, имеющих по трём взаимоперпендикулярным направлениям при x=0 Z_{a max}(нТл)=200H/h³ размерыодного порядка, с отдалением от этих тел приближается к аномалии шара.

Ур-е, определяющее U-потенциал магнитного поля шара во внешней точке, проще всего получить переходом от потенциала гравитационного поля V с использованием уравнения Пуассона:

Поскольку шар как источник гравитационного поля эквивалентен точечному источнику с той же массой, потенциальная функция имеет вид:

, где m’- масса шара, равная произведению избыточной плотности σ’ на объём V_m, т.е. m’= σ’V_m; r- расстояние от центра шара до рассматриваемой точки; r²=z²+h²; z=h – глубина залегания центра шара; x-абсцисса рассматриваемой точки, отсчитанная от эпицентра шара; G- постоянная тяготения.

И ,

Где M=J*V_Ш – магнитный момент шара.

Потенциальная функция примет вид

Продифференцировав по z и x, получим уравнения для составляющих вектора напряжённости:

Для перехода к составляющим вектора магнитной индукции, выраженной в нанотесла, достаточно умножить правые части на “ ”. Получим:

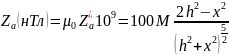
При решении обратной задачи имеется возможность определить глубину залегания центра шара. Для этого можно использовать, например, x_0.5 графика Z_а или l графика H_a.

или h=l

Зная h, можно определить магнитный момент шара:

По аномалии нельзя найти ни объём шара, ни его намгниченность, ни глубину до верхней кромки.

При известном значении намагниченности, установленном, например, в результате изучения образцов из скважин, пробуренных в пределах подобных аномалий на соседнем участке, можно вычислить объём шара V_Ш, радиус шара R_Ш, глубину залегания верхней кромки h_1.

В этом случае так же можно вычислить количество руды m’, если аномалия обусловлена рудным телом.

m’=V_Ш*d, где d- плотность руды.