3.3 Методы решения задачи.
Интегрируется система дифференциальных уравнений методом Эйлера:
Hi+1 = Hi + ∆t
Hi+1 = Hi + ∆t
= с1 Рвпi+1 = Рвпi + c1i∆t
= с2 Рб i+1 = Рб i + с2i∆t
= c3 r1i+1 = r1i + c3i∆t
= c4 φ1i+1 = φ1i + c4i∆t
= c5 r2i+1 = r2i + c5i∆t
= c6 φ2i+1 = φ2i + c6i∆t
где с1,c2,c3,…,c6 – результаты решения системы линейных алгебраических уравнений:
a11 + а12 + а13 + a14 + a15 + a16 = b1,
… …………………………………………………
……………………………………………………
……………………………………………………
a61 + a62 + а63 + a64 + a65 + a66 = b6.
На каждом шаге интегрирования (метод Гаусса с выбором главного элемента).
Интегрирование проводится до момента времени, когда воздушная подушка полностью не опустится на поверхность.
Исходные данные:
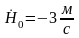
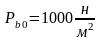
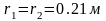
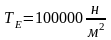
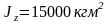
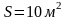
Геометрические данные и массовые данные: S0, BB’, m.
m
= 270
,
ВВ’ = 1.9м,
S0 = 0.123375236м2,
L0нат = 0,96629434м.
Параметры состояния:
Ратм
= 100000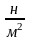
,
ρатм
= 1,25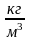
3.4 Анализ результатов
Решая данную систему уравнений на компьютерном языке программирования PASCAL, получаем следующие результаты:
1) Зависимость давления в баллоне от времени.
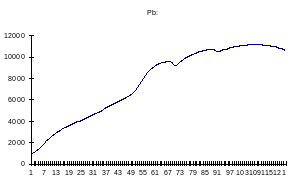
2) Зависимость давления в воздушной подушке от времени.
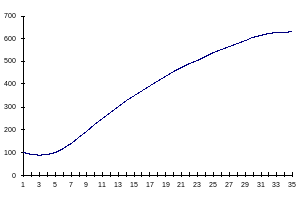
Высота.
Угол.
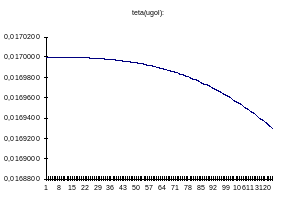
Угловая скорость.
Центральные радиусы и углы.
f2: |
f1: |
r1: |
r2: |
2,300000 |
2,30000000 |
0,2100000 |
0,21000000 |
2,309805 |
2,30074140 |
0,2090455 |
0,20175991 |
2,319839 |
2,30145621 |
0,2081165 |
0,19374534 |
2,329694 |
2,30210956 |
0,2072472 |
0,18633037 |
2,338907 |
2,30266952 |
0,2064694 |
0,17986703 |
2,347107 |
2,30311823 |
0,2058011 |
0,17456462 |
2,354120 |
2,30345521 |
0,2052434 |
0,17044719 |
2,359950 |
2,30369181 |
0,2047855 |
0,16740812 |
2,364700 |
2,30384358 |
0,2044123 |
0,16529104 |
2,368504 |
2,30392537 |
0,2041094 |
0,16394218 |
2,371494 |
2,30394963 |
0,2038646 |
0,16323100 |
2,373787 |
2,30392619 |
0,2036683 |
0,16305332 |
2,375479 |
2,30386263 |
0,2035129 |
0,16332811 |
2,376650 |
2,30376476 |
0,2033928 |
0,16399293 |
2,377365 |
2,30363702 |
0,2033036 |
0,16499970 |
2,377677 |
2,30348284 |
0,2032420 |
0,16631130 |
2,377630 |
2,30330483 |
0,2032052 |
0,16789895 |
2,377262 |
2,30310507 |
0,2031914 |
0,16974017 |
2,376603 |
2,30288517 |
0,2031989 |
0,17181713 |
2,375682 |
2,30264644 |
0,2032265 |
0,17411532 |
2,374524 |
2,30239000 |
0,2032730 |
0,17662233 |
2,373151 |
2,30211690 |
0,2033375 |
0,17932659 |
2,371588 |
2,30182818 |
0,2034189 |
0,18221620 |
2,369860 |
2,30152505 |
0,2035161 |
0,18527748 |
2,367996 |
2,30120900 |
0,2036275 |
0,18849351 |
2,366026 |
2,30088191 |
0,2037513 |
0,19184254 |
2,363988 |
2,30054621 |
0,2038848 |
0,19529657 |
2,361925 |
2,30020496 |
0,2040251 |
0,19882029 |
2,359884 |
2,29986185 |
0,2041681 |
0,20237085 |
2,357915 |
2,29952113 |
0,2043093 |
0,20589876 |
2,356070 |
2,29918744 |
0,2044439 |
0,20935003 |
2,354398 |
2,29886552 |
0,2045666 |
0,21266922 |
2,352942 |
2,29855993 |
0,2046726 |
0,21580278 |
2,351740 |
2,29827481 |
0,2047573 |
0,21870182 |
8) Перегрузка = 0,8
Полученные результаты не противоречат ограничениям системы (краевым условиям):
Центральные радиусы и углы не могут быть отрицательными.
0 < Pвп < 3000…10000
перегрузка не должна превышать 3х единиц
СПИСОК ЛИТЕРАТУРЫ
1.Воронков И.М. Курс теоретической механики – М.: ГИФМЛ. 1961
2.Меркин Д.Р. Введение в механику гибкой нити – М.: Наука. Главная редакция физико-математической литературы, 1980.
3.Турчак Л.И. Основы численных методов – М.: Наука. Главная редакция физико-математической литературы, 1987.
Размещено на Allbest.ru