3. Анализ решения задачи

Первые шесть уравнений имеют вид:

P 1r1 + P1f(Xo2 – Xo1) = (P1 – P2)r2; (a)

r2(1 – cosφ2) = H + YA; (б)

r1(1 – cosφ1) = H + YB; (в) (17)

Xo1 = XB + r1sinφ1; (г)

Xo2 = XA – r2sinφ2 (д)

(е)

После исключения Xo1 и Xo2 получаем:

r1φ1 + XA – r2sinφ2 – XB – r1sinφ1 + r2φ2 = l0

Выражая из уравнения (17 б, в)

,

и подставляя выражения r1 и r2 в уравнения, имеем:

(I)

Получили систему (I), состоящую из двух нелинейных алгебраических уравнений с двумя неизвестными j1 и j2.

Обозначим первое уравнение системы (I) за f1(φ1,φ2) = 0, а второе за f2(φ1,φ2) = 0. Затем дифференцируем функции f1 и f2 по φ1 и φ2. Полученные производные подставляем в уравнения на шаге:

.

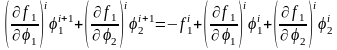
Проведенный анализ системы показал, что аналитического решения построить не удается. Поэтому решение задачи осуществляется численно.

Численное решение задачи организовано следующим образом. Задавая начальное приближение избыточного давления в пневмооболочке P1(1) и, решая нелинейную систему (I), определяем геометрические характеристики поперечного сечения (j1, j2, r1, r2, Xo1, Xo2, dl, N). Далее, по найденным геометрическим характеристикам, определяем площадь поперечного сечения по формуле:

. (16)

и используя, на основании закона сохранения массы воздуха, предварительно закаченного в пневмооболочку, уравнение:

(PАТМ + P1)(S0L)n=(PАТМ + P2)(SL)n (2)

(где n – показатель адиабаты (для воздуха n=1,4), L – длина оболочки, S0,S – площади, ограниченные нитью ABCD и платформой AB в начальном и исследуемом состоянии) находим откорректированное значение P1(2) . Если разность по абсолютной величине между P1(1) и P1(2) меньше некоторого числа d, где d - заданная величина, то значения, полученные при этом решении, будем считать конечными. Если условие не выполняется, то решаем все заново с новым значением P1(1) и т.д.

5. Обзор методов решения

1.4.1 Метод половинного деления (для уравнения)

Y

C₀ A

0 B C X

рис.3

Это один из надежных методов решения нелинейных уравнений. Он состоит в следующем. Допустим, что нам удалось найти отрезок [A , B] , в котором расположено искомое значение корня x=C, т.е. A<C<B (рис.3). В качестве начального приближения корня С0 принимаем середину этого отрезка, т.е. . Далее исследуем значение функции F(x) на концах отрезков [A , C0] , [C0 , B] , в точках A , C0 , B . Тот из них, на концах которого F(x) принимает значения разных знаков, содержит искомый корень, поэтому его принимаем в качестве нового отрезка. Вторую половину отрезка [A , B] на которой знак F(x) не меняется, отбрасываем. В качестве первой итерации корня принимаем середину нового отрезка и так далее. Таким образом, после каждой итерации отрезок, на котором расположен корень, уменьшается вдвое, т.е. после n итераций он сокращается в 2n раз.