9. Связь напряженности и потенциала однородного электростатического поля

Т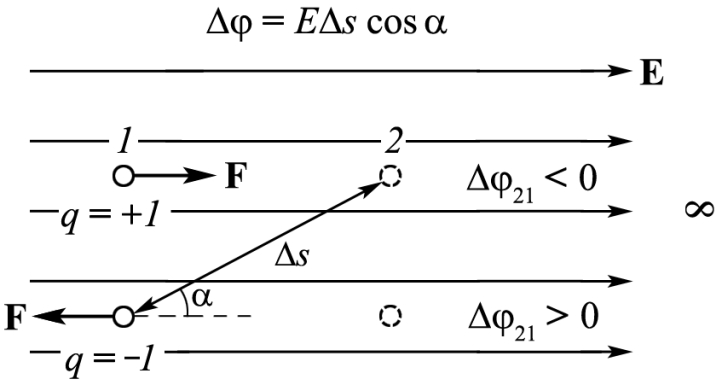 еорема физики (формула) и словесная формулировка математической записи: Δφ ≡ E∆sּcosα. Разность потенциалов между двумя точками пространства и напряженность электрического поля связаны между собой так же, как работа и сила.

Доказательство теоремы. Вывод формулы: согласно предыдущей теореме Δφ = ; по определению работы для постоянной силы распишем: Δφ =

Сила остается постоянной, поскольку напряженность постоянна, а F = = Eq; напряженность остается постоянной, поскольку по условию поле однородно. Теорема доказана.

Условия выполнения: формула выполняется для однородного поля.

10. Связь силовых линий и эквипотенциальных поверхностей электростатического поля

Теорема физики (формула) и словесная формулировка математической записи: силовые линии электростатического поля перпендикулярны эквипотенциальным поверхностям.

Доказательство теоремы. Вывод формулы: анализ формулы предыдущего пункта показывает, что силовые линии электростатического поля перпендикулярны эквипотенциальным поверхностям. Действительно, поскольку потенциалы всех точек эквипотенциальной поверхности одинаковы, то при перемещении по эквипотенциальной поверхности Δφ = = φ₂ − φ₁ = 0, значит E dsּcos α = 0, причем E ≠ 0 – поле есть, ds ≠ 0 – мы движемся по эквипотенциальной поверхности, равняться нулю может только cos α: cos α = 0 α = 90°.

Эквипотенциальные поверхности перпендикулярны силовым линиям. Теорема доказана.

Условия выполнения: утверждение выполняется всегда.

11. Потенциал поверхности уединенного проводника

Теорема физики (формула) и словесная формулировка математической записи: поверхность уединенного проводника любой формы есть эквипотенциальная поверхность.

Д оказательство теоремы. Вывод формулы: доказательство утверждения логическое: если бы между некоторыми двумя точками поверхности проводника существовала не равная нулю разность потенциалов, то заряды в проводнике двигались бы от большего потенциала к меньшему до тех пор, пока потенциалы не выровнялись бы.

Условия выполнения: утверждение выполняется всегда.

12. Потенциал объема уединенного проводника

Т еорема физики (формула) и словесная формулировка математической записи: потенциал уединенного проводника во всем объеме есть величина постоянная.

Доказательство теоремы. Вывод формулы: доказательство этого утверждения логическое: если бы между некоторыми двумя точками объема проводника существовала не равная нулю разность потенциалов, то заряды в проводнике двигались бы от большего потенциала к меньшему до тех пор, пока потенциалы не выровнялись бы.

Поле внутри проводящей сетки отсутствует. В этом состоит принцип электростатической защиты.

Условия выполнения: формула выполняется всегда.

13. Ёмкость шара

Т еорема физики (формула) и словесная формулировка математической записи: ёмкость шара С равна , где r – радиус шара, ε– диэлектрическая проницаемость среды, ε₀ – электрическая постоянная.

Доказательство теоремы. Вывод формулы: по определению емкости уединенного проводника емкость шара С равна отношению заряда q к потенциалу на шаре φ:

. (1)

Потенциал шара равен потенциалу точечного заряда, сосредоточенного в его центре (эта теорема доказывается в ВУЗе)

, (2)

где r – радиус шара. Подставляя (2) в (1), получаем искомую формулу . Теорема доказана.

Условия выполнения: формула выполняется всегда.