6. Потенциал точечного заряда

Т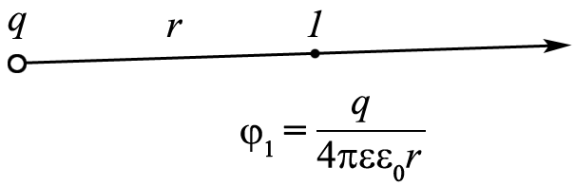 еорема физики (формула) и словесная формулировка математической записи: потенциал φ₁ некоторой точки 1 поля, созданного точечным зарядом q, равен φ₁ = .

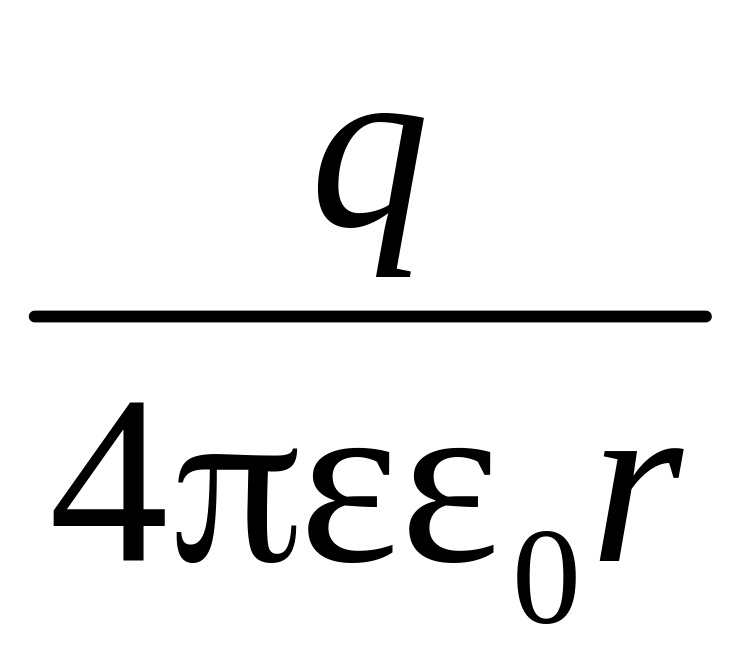Доказательство теоремы. Вывод формулы: по определению потенциала φ₁ = , где W₁ = A_1∞; по определению работы для силы Кулона

А_1∞ = ; φ₁ = . Теорема будет доказана, как только на занятиях по математике в теме «интеграл» Вы докажете, что для достаточно малых ∆r

.

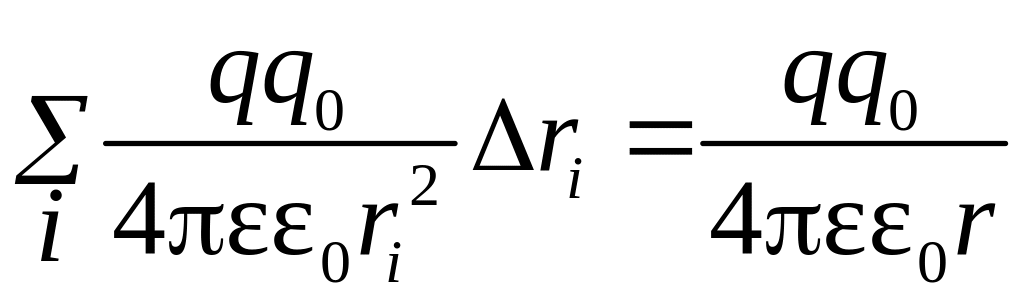Условия выполнения: формула выполняется для точечного заряда.

7. Потенциал суммы точечных зарядов

Теорема физики (формула) и словесная формулировка математической записи: φ₁ = = φ₁₁ + φ₂₁ + φ₃₁ +…+ φ_i1 +… Потенциал электрического поля, создаваемый суммой точечных зарядов 1, 2, 3…, i … в данной точке пространства 1, φ₁, равен сумме потенциалов полей, создаваемых каждым из этих точечных зарядов в точке 1− .

Доказательство теоремы. Вывод формулы: по определению потенциала φ = (1)

− потенциал равен потенциальной энергии заряда, помещенного в данную точку пространства, деленной на этот заряд.

По определению потенциальная энергия электростатического поля равна работе электрических сил по перемещению данного заряда из точки 1 пространства в бесконечность:

W₁ = A_1∞. (2)

Работа электрических сил равна сумме работ на малых участках пути (результирующая сила Кулона может быть разной на этих малых участках). Сила Кулона создаётся зарядами q₁, q₂, q₃,…, q_i,…

(3)

для скалярного произведения выполняется распределительный закон:

=

= . (4)

З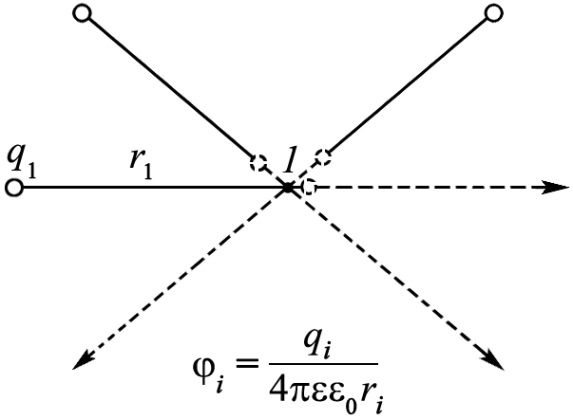 десь первое слагаемое есть работа вдоль пути от данной точки пространства 1 до бесконечности для силы Кулона между первым зарядом q₁, создающим поле, и зарядом, помещенным в точку 1, − A_11∞, второе слагаемое есть работа вдоль этого же пути для силы Кулона между вторым зарядом, создающим поле, и зарядом, помещенным в точку 1, − A_21∞ и т.д. Таким образом,

A _1∞ = A_11∞ + A_21∞ +…+ A_i1∞ +… (5)

Подставим (5) в (2) и (2) в (1). Следуя определениям потенциальной энергии и потенциала, получаем искомую формулу:

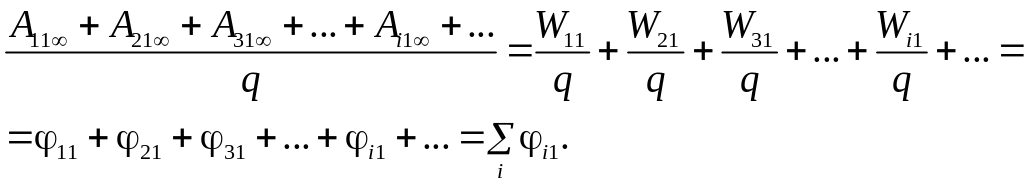
Теорема доказана.

Условия выполнения: формула выполняется всегда.

8. Связь разности потенциалов и работы электрических сил

Теорема физики (формула) и словесная формулировка математической записи: φ₁ − φ₂ ≡ Δφ ≡ . Разность потенциалов между двумя точками пространства численно равна работе электрических сил по перенесению заряда q из точки 1 в точку 2, деленной на величину этого заряда.

Доказательство теоремы. Вывод формулы: по определению потенциала и потенциальной энергии

φ₁ − φ₂ ≡ Δφ₁₂ ≡ U = ,

А_1∞ = A₁₂ + A_2∞, поэтому A_1∞ − A_2∞ = (A₁₂ + A_2∞)A_2∞ = А₁₂. Δφ = . Теорема доказана.

Следствие: разность потенциалов между двумя точками поля численно равна работе по перенесению пробного заряда из одной точки в другую. Это следует из формулы: Δφ = .

Условия выполнения: формула выполняется всегда.