§7. Формулы кинематики и динамики

1. Первая космическая скорость

Т еорема физики. Формула и словесная формулировка математической записи: , v_1к= . Первая космическая скорость – это наименьшая скорость, с которой спутник может вращаться на орбите Земли по окружности.

Д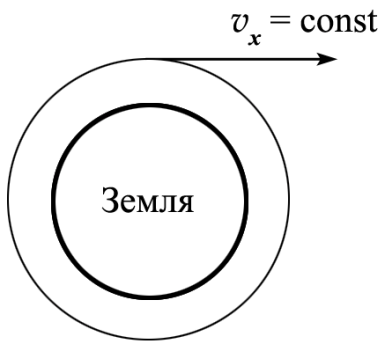 оказательство теоремы. Вывод формулы: чем с большей скоростью бросить камень в горизонтальном направлении, тем шире парабола, по которой камень летит к Земле. При некоторой скорости парабола зайдет за земной шар, и камень превратится в спутник Земли.

Чтобы повернуть тело, нужно приложить силу (это знают те, кто, например, удерживал на круговой траектории модель самолета). При движении тела по окружности с постоянной скоростью оно (тело) изменяет направление скорости за счет какой-либо силы, приложенной перпендикулярно скорости тела, таким образом, тело приобретает нормальное ускорение.

Нормальной (т.е. перпендикулярной скорости движения) силой для спутника Земли выступает гравитационная сила притяжения к Земле. Как доказано в предыдущем пункте, нормальное ускорение но, с другой стороны, по второму закону Ньютона F_G=ma_n. . Откуда . Подставляя значение , имеем . v_1к= . Теорема доказана.

Условия выполнения: формула выполняется всегда.

§8. Формулы динамики

1. Потенциальная энергия вблизи поверхности Земли

Теорема физики. Формула и словесная формулировка математической записи: Е_п mgh. Потенциальная энергия вблизи поверхности Земли равна силе тяжести mg, помноженной на расстояние между нижней и верхней горизонталями, между которыми перемещается тело. Значение потенциальной энергии на нижней горизонтали при решении задач принимается равным нулю.

Доказательство теоремы. Вывод формулы: потенциальная энергия вблизи поверхности Земли измеряется работой, которую может совершить тело при переходе с некоторой горизонтали на нулевую горизонталь (нулевой уровень). Е_п = А, если тело свободно падает (рис. а), то А = FS cos , где F = mg, S = h, cos α = cos 0 = 1, E_п= А = mgh.

Е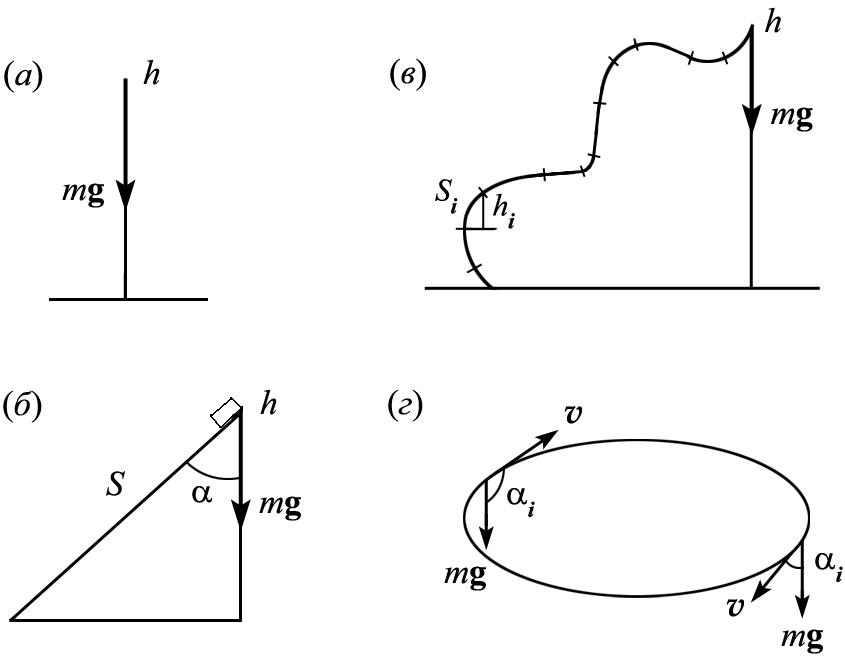 сли тело соскальзывает без трения по наклонной плоскости (рис. б), то

А = FS cos α, где F = mg,

a S·cosα=h (h − прилежащий катет прямо-угольного треугольника). Е_п = A = mgh.

Если тело движется по произвольной траектории (рис. в), то мы разбиваем траекторию на прямолинейные участки для каждого из которых = mgh_i, а для всего криволинейного участка пути Е_п = = mgh.

Работа силы тяжести по замкнутому контуру равна нулю. Так как, когда тело опускается (рис. г), угол _i острый, cos_i  0 и работа положительная, а когда тело поднимается, угол между направлением силы и перемещением S тупой, cos_i  0 и работа отрицательная (h_i, соответственно, берутся со знаками «+» или «−»). Для замкнутого пути суммарные величины h подъемов и спусков одинаковы, и суммарная работа равна нулю.

Условия выполнения: выполняется вблизи поверхности Земли и вблизи поверхности любой планеты (g имеет свое значение для разных планет).

2. Закон сохранения импульса

Теорема физики. Формула и словесная формулировка математической записи: Р = р₁ + р₂ + р₃ = const. В замкнутой изолированной системе тел суммарный импульс системы материальных точек сохраняется.

Доказательство теоремы. Вывод формулы: нередко встречается ситуация, когда некоторое количество тел, например три тела, взаимодействуют друг с другом и пренебрежимо слабо взаимодействуют с внешней средой. Такие тела выделяются в замкнутую, изолированную систему. Для каждого из тел такой системы запишем второй закон Ньютона.

Силы, с которыми выделенные в систему тела действуют друг на друга F_ij, называются внутренними силами системы; силы, действующие на выделенные тела со стороны других тел F_сторi, называются сторонними.

F_рез1 = m₁a₁, F_рез1 = F_стор1 + F₁₂ + F₁₃; .

F_рез2 = m₂a₂, F_рез2 = F_стор2 + F₂₁ + F₂₃; .

F_рез3 = m₃a₃, F_рез3 = F_стор3 + F₃₁ + F₃₂; .

Для замкнутой изолированной системы

F_стор1 = 0, F_стор2 = 0, F_стор3 = 0.

Здесь F_стор1 – результирующая сила, действующая со стороны внешних по отношению к системе тел на тело 1; F_стор2 − на тело 2; F_стор3 − на тело 3.

F₁₂ − сила, действующая со стороны тела 2 на тело 1;

F₁₃ − сила, действующая со стороны тела 3 на тело 1;

F₂₁ − сила, действующая со стороны тела 1 на тело 2;

F₂₃ − сила, действующая со стороны тела 3 на тело 2;

F₃₁ − сила, действующая со стороны тела 1 на тело 3;

F₃₂ − сила, действующая со стороны тела 2 на тело 3.

F_стор1 + F₁₂ + F₁₃= m₁a₁=m₁ .

Для F_рез2 и F_рез3, проведя такие же рассуждения, получим систему из трех уравнений:

F_стор1 + F₁₂ + F₁₃=

F_стор2 + F₂₁ + F₂₃=

F_стор3 + F₃₁ + F₃₂=

Алгебраически почленно сложим эти векторные уравнения. Мы не имеем права складывать эти уравнения векторно, поскольку силы приложены к разным материальным точкам. Математически не доказано, что алгебраическое сложение в этом случае правомерно. Но во всех учебниках доказательство приведено именно в таком виде. Иного доказательства нет.

С илы F₁₂ = −F₂₁, F₁₃ = −F₃₁ и F₂₃ = −F₃₂ − по третьему закону Ньютона, поэтому после сокращения получим: F_стор·Δt = Δp₁+Δp₂+Δp₃, где F_стор = F_стор1 + F_стор2 + F_стор3. F_стор = 0, т.к. система замкнутая, изолированная, значит Δp₁+Δp₂+Δp₃=0.

Распишем, чему равна разность суммарных импульсов системы по определению:

_ΔP=(p_к1+ p_к2+ p_к3) (p_н1+ p_н2+ p_н3) = (p_к1 p_н1)+ (p_к2 p_н2)+ (p_к3 p_н3).

Значит,

F_стор·Δt =0=Δp₁+Δp₂+Δp₃=ΔP_.

Закон доказан.

Следствие если F_стор  0, но время их действия мало, то t  0 и F_сторt  0. При стремлении времени действия внешних сил к нулю (t  0) суммарный импульс системы тоже сохраняется.

Условия выполнения: есть два случая применения этого закона.

1. Внешних сил нет или их действие скомпенсировано – рассматривается замкнутая изолированная система.

2. Внешние силы присутствуют, но время действия внешних сил достаточно мало.