21. Взаимная индуктивность.

Рис. 21.1. Магнитные потоки катушек. Случай М > 0.

Рис. 21.2. Маркировка катушек. Случай М > 0.

Рис. 21.3. Маркировка катушек. Случай М < 0.

Рассмотрим две магнитно связанные катушки индуктивности. Магнитный поток каждой из них частично проходит через другую катушку (рис. 21.1, 21.2). Поэтому ток первой катушки посредством магнитного поля вследствие явления электромагнитной индукции создает на зажимах второй катушки напряжение , где М – коэффициент взаимной индуктивности. Он измеряется в генри (Гн). Ток второй катушки создает на зажимах первой напряжение .

Кроме того, напряжения на катушках создаются вследствие изменения своих собственных токов, поэтому

, .

Знак М зависит от взаимного расположения катушек, а также от выбора направлений стрелок тока и напряжений. Стрелки напряжений, как правило, направляют согласно стрелкам тока (рис.21.1), и часто вообще не показывают на схеме в явном виде.

Если магнитные поля, создаваемые положительными токами катушек, в области самих катушек складываются, то М > 0 (рис.21.1, 21.2), а если вычитаются, то M < 0 (рис.21.3).

На схемах эл. цепей взаимное расположение катушек показывается с помощью маркировки. "Начала" обмоток отмечаются точками. Если стрелки токов обеих катушек направлены от "начал" к "концам" или от "концов" к "началам", то M > 0 (рис.21.2). Если у одной катушки стрелка тока направлена от "начала" к "концу", а у другой наоборот, то M < 0 (рис.21.3).

Если сразу несколько катушек имеют магнитную связь, то их начала маркируются отдельно для каждой пары.

Если магнитный поток первой катушки полностью проходит через вторую (соответственно, поток второй катушки полностью проходит через первую), то - это так называемый "идеальный трансформатор". Значение М не может быть больше. Реально оно всегда меньше указанного значения из-за того, что магнитные потоки катушек никогда в точности не могут совпадать. Последнюю формулу легко доказать с помощью теории магнитных цепей.

Приложение.

Комплексные числа.

Введение.

Комплексные числа имеют три формы записи. Алгебраическая форма представляет число в виде ; здесь a и b – действительные числа, i – число иного рода, называемое мнимой единицей. Основное свойство числа i состоит в том, что его квадрат равен минус единице: . Числа вида являются действительными. Числа вида называются мнимыми.

Обозначим число буквой z . Число a называется действительной частью числа z, число b – мнимой частью числа z . Коротко это можно записать так: , , где Re и Im – принятые в математике обозначения действительной и мнимой части комплексного числа.

Рис. 1. Комплексная плоскость и ее оси.

Число z можно понимать как упорядоченную пару действительных чисел . Поэтому его можно изобразить точкой на плоскости. Действительная часть откладывается по оси абсцисс, а мнимая часть – по оси ординат (рис. 1).

Комплексное число чаще изображают не точкой, а вектором, начало которого совпадает с началом координат комплексной плоскости, а конец имеет декартовы координаты . Если такой вектор перенести параллельно самому себе, он также будет изображать то же самое число.

Точку на плоскости можно рассматривать и в полярных координатах , где  – расстояние от точки до начала координат,  – угол между отрезком, соединяющим точку с началом координат, и осью абсцисс (рис. 1).

Число  называется модулем числа z , число  называется аргументом (или фазой) числа z . Коротко это обозначается так: , .

Из рис. 1 видно, что

, , (1)

поэтому комплексное число z можно представить в виде

Такая форма представления комплексного числа называется тригонометрической.

Отметим, что . (2)

Формулы (1) определяют переход от тригонометрической формы комплексного числа к алгебраической, формулы (2) – от алгебраической к тригонометрической. При этом  лежит в пределах от – до  и вычисляется с учетом знаков a и b :

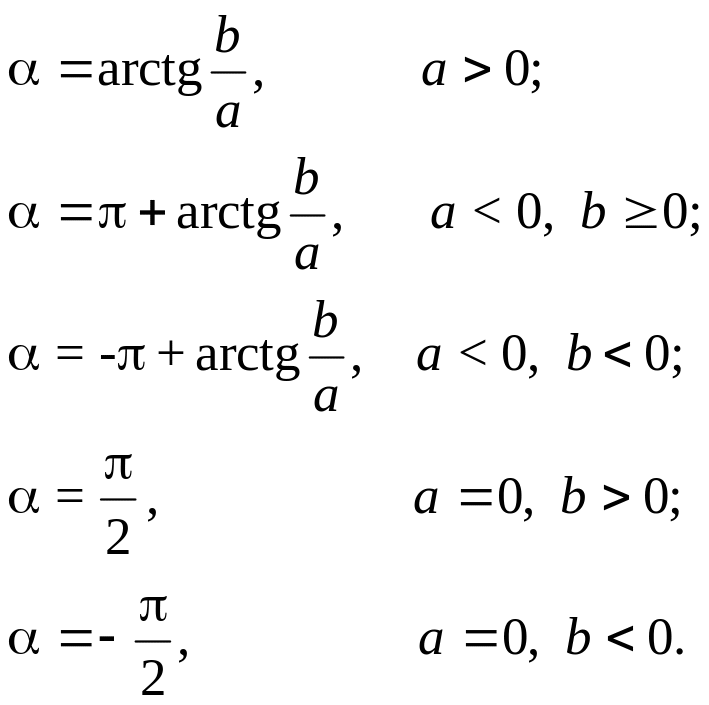
Для числа аргумент не определен.

Формула Эйлера позволяет ввести показательную форму комплексного числа: . Модуль  и фаза  имеют тот же смысл, что и для тригонометрической формы комплексного числа.

Формулу Эйлера можно понимать как определение экспоненты с мнимым показателем: – это такое комплексное число, действительная часть которого равна , а мнимая равна . Более корректно функция определяется как сумма ряда

.

Учитывая, что и сгруппировав отдельно действительные и мнимые слагаемые этого ряда, получим ряды для косинуса и синуса, что и доказывает формулу Эйлера (строго говоря, такая перегруппировка слагаемых нуждается в обосновании, но мы законность этого действия примем без доказательства):

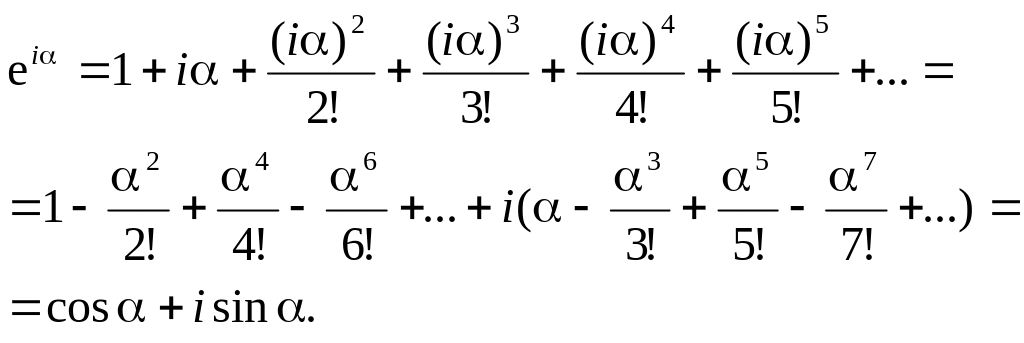
Для экспоненты с мнимым показателем, так же как и для экспоненты с действительным показателем, справедливо свойство: произведение двух экспонент равно экспоненте, показатель которой равен сумме показателей сомножителей:

.

Сложение комплексных чисел

Рис. 2. Сложение комплексных чисел на плоскости.

Суммой комплексных чисел и называется комплексное число .

То есть, действительная часть суммы – это сумма действительных частей слагаемых, а мнимая часть суммы – это сумма мнимых частей слагаемых.

Например, если , то .

На комплексной плоскости сложению комплексных чисел соответствует сложение векторов (рис. 2).

Сложение чисел в показательной и тригонометрической форме неудобно. Чтобы сделать это, нужно сначала перевести оба числа в алгебраическую форму, сложить их, а затем перевести результат в нужную форму.

Например,

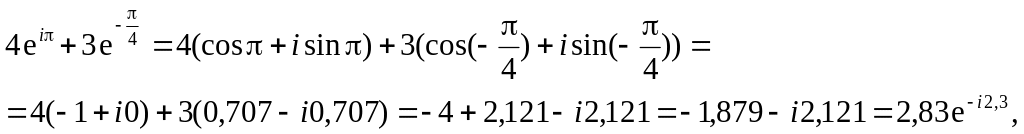
Умножение комплексных чисел

Умножение комплексных чисел в алгебраической форме выполняется по тем же правилам, что и умножение действительных чисел. Единственное различие в том, что :

.

Например, .

Умножение комплексных чисел в показательной форме выполняется еще проще. Пусть , тогда

,

то есть, при умножении комплексных чисел модуль произведения равен произведению модулей сомножителей, а аргумент произведения равен сумме аргументов сомножителей.

Например, ; .

С помощью формулы Эйлера из правила умножения комплексных чисел в показательной форме может быть получено правило умножения комплексных чисел в тригонометрической форме. Оно такое же, как для чисел в показательной форме.

Замечание 1: Мнимая единица может записываться как перед действительным множителем, так и после него: и т.д. Эти выражения равны вследствие того что произведение любых двух комплексных чисел коммутативно, т.е не зависит от порядка сомножителей.

Замечание 2: Аргументы комплексных чисел могут выражаться как в радианах (то есть просто в числах), так и в градусах. Запись аргументов комплексных чисел в радианах, как правило, применяется в математике и физике; запись в градусах – в технических науках и инженерных расчетах.

Умножению комплексного числа z на число соответствует растяжение вектора, изображающего число z, в раз и поворот его на угол . Это следует из описанных выше правил умножения.

Деление комплексных чисел

Проще всего делить числа в показательной и тригонометрической форме. При этом модуль частного равен отношению модулей делимого и делителя, аргумент частного равен разности аргументов делимого и делителя. Это правило прямо следует из правил умножения.

Пусть , , тогда .

Например, .

Чтобы разделить комплексное число в алгебраической форме на действительное число, нужно разделить отдельно действительную и мнимую часть. Пусть , тогда . Например: .

Деление комплексного числа в алгебраической форме на комплексное число в алгебраической форме сводят к делению комплексного числа на действительное. Это делают путем умножения числителя и знаменателя на число, комплексно сопряженное знаменателю.

Рис. 3. сопряженные комплексные числа.

Комплексно сопряженное число обозначается звездочкой или чертой наверху, например, . Комплексно сопряженные числа имеют одну и ту же действительную часть и противоположные мнимые части: . На комплексной плоскости комплексно сопряженные числа расположены симметрично относительно действительной оси (рис. 3). Произведение числа на его сопряженное равно квадрату его модуля, это всегда неотрицательное действительное число:

.

Итак, разделим два числа в алгебраической форме. Пусть

, .

Тогда .

Например, .

50