Федеральное агентство по образованию

Государственное образовательное учреждение

Высшего профессионального образования

НИЖЕГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ

ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ им. Р.Е. Алексеева

Кафедра Информатики и систем управления

ТЕХНОЛОГИЯ ПРОГРАММИРОВАНИЯ

Методические указания к выполнению курсовых работ

для студентов специальностей 2202.00 “Автоматизированные системы обработки информации и управления” и 0719.00 “Информационные системы” очной и вечерней форм обучения

Нижний Новгород

2007

Составитель С.Н. Капранов

УДК 681

Технология программирования: метод. указания к выполнению курсовых работ для студентов спец. 2202.00 “Автоматизированные системы обработки информации и управления” и 0719.00 “Информационные системы” очной и вечерней форм обучения /НГТУ; Сост.: С.Н. Капранов, Н.Новгород. 2007. – 18 с.

Приведены методические рекомендации и задания для выполнения курсовых работ по курсу “ Технология программирования ” в соответствии с учебным планом специальностей 2202.00 “Автоматизированные системы обработки информации и управления” и 0719.00 “Информационные системы”.

Могут быть использованы для проведения курсовых работ по аналогичным курсам других специальностей.

Научный редактор Ю.С.Бажанов

Редактор Э.Б. Абросимова

Подп. в печ. 8.10.07 Формат 60x84 ¹/16. Бумага газетная. Печать офсетная. Печ.л. 1. Уч.-изд.л. 0,5. Тираж 100 экз. Заказ.

________________________________________________________

Нижегородский государственный технический университет им. Р.Е. Алексеева

Типография НГТУ.603950,Н.Новгород,ул.Минина,24.

© Нижегородский государственный

технический университет

им. Р.Е. Алексеева, 2007

ВВЕДЕНИЕ

Цель данной курсовой работы состоит в закреплении теоретических основ курса “Технология программирования” – разработка игровой программы на основе базовых “быстрых” алгоритмов, приобретение практических навыков по проектированию удобного пользовательского интерфейса, разработки алгоритмов и документировании программных средств.

Перед выполнением курсовых работ студенты должны пройти инструктаж по технике безопасности и расписаться в соответствующем контрольном листе инструктажа.

ПОРЯДОК ВЫПОЛНЕНИЯ КУРСОВЫХ РАБОТ

1. Получить у преподавателя вариант задания к курсовой работе.

2. Ознакомится с правилами игры.

3. Разработать удобный пользовательский интерфейс. Пользователь игровой программы должен иметь возможность пользоваться как клавиатурой, так и мышью.

4. Разработать структуры данных для оперирования такими понятиями как состояние игры, дерево игры, ход игрока и т.д.

5. Разработать оценочную функцию хода игрока.

6. Разработать алгоритм поиска лучшего хода для игрока (компьютера).

7. Разработать и добавить в алгоритм генерации хода алгоритм быстрого нахождения ситуаций, которые уже были рассмотрены (если требуется).

8. Разработать документацию, состоящую из:

   1. Правил игры.

   2. Инструкции пользователя, описывающей как пользоваться программой.

   3. Инструкции программиста, описывающей используемые структуры данных, классы, функции.

9. Оформить отчёт по курсовой работе.

При разработке программы особое внимание уделить следующим моментам.

• игровая программа должна иметь несколько уровней сложности;

• должна быть предусмотрена возможность отката игры на несколько ходов назад;

• требования к функциям:

• она должна выполнят только одну задачу;

• тело функции должно быть хорошо комментировано. Комментарии должны указывать цель действия операторов, назначение переменных и пояснять логику программы;

• она должна быть максимально понятна и удобочитаема;

• программа должна быть написана с использованием принципа защитного программирования. То есть должна быть обеспечена обработка некорректных данных.

ОФОРМЛЕНИЕ ОТЧЁТОВ

В отчёте должен быть титульный лист, на котором необходимо указать название курсовой работы, Ф.И.О. студента и номер учебной группы.

Отчёт должен состоять из:

1. Введения.

2. Правил игры.

3. Инструкция пользователя.

4. Инструкция программиста.

5. Распечатка программы.

6. Распечатка внешнего вида программы.

АЛГОРИТМ ИГРОВОГО ПОИСКА ЛУЧШЕГО ХОДА

Во всех случаях исходят из начального состояния, которое может быть обычным состоянием начала игры. Задача алгоритма – найти наилучший возможный ход, исходя из этого состояния для заданного игрока.

Состояние s – это описание игры на какой-то момент (клетки заняты различными фигурами, поле игры некоторым образом заполнено крестиками и ноликами и т.д.)

Тип игрок может иметь два состояния – “компьютер” и “человек”.

Задача алгоритма состоит в построении воображаемого дерева различных возможных ходов, возможных ответов человека на каждый из них и т.д.

Алгоритм должен найти оптимальный ход из любой игровой ситуации. Он должен “вообразить” возможное развёртывание игры для каждого допустимого хода:

• если нет ни одного допустимого хода, то игра проиграна;

• если возможны n ходов, то исследуются новые состояния s₁,s₂,…,s_n, вытекающие из этих ходов.

Для каждого из этих ситуаций алгоритм проверяет возможные ответы воображаемого противника:

• если у него нет возможного ход, то рассматривается состояние выигрышное или ничейное;

• в противном случае необходимо рассмотреть различные возможные ходы для противника.

Это приводит к рассмотрению дерева игры.

Вершины соответствуют компьютеру и человеку. Вершина компьютера выигрывает, если выигрывает по крайней мере один из её сыновей. Вершина человека выигрывает (у компьютера), если выигрывают все её сыновья. Листья соответствуют конечным ситуациям, представляющие выигрышные или проигрышные для компьютера партии игры.

Построенное таким образом дерево является конечным для всех обычных игр, если ввести некоторое количество правил, для того чтобы избежать бесконечного зацикливания (например, в шахматах они явно присутствуют).

В реальных играх дерево решений может быть слишком большим. В этом случае вводится некоторый критерий, который позволяет остановить построение дерева решений в вершинах, которые рассматриваются как конечные.

В большинстве случаев критерием выступает глубина вершины m, относительно начального состояния s. Величина m выбирается в зависимости от ограничений по времени.

В этом случае конечная вершина дерева игры очень редко будет “выигрывающей” или “проигрывающей”. Для того чтобы классифицировать различные возможные ходы, необходимо каждой конечной вершине поставить в соответствие некоторое положительное или отрицательное число. Это значение будет тем больше, чем благоприятнее ситуация в этой вершине для “компьютера” и тем меньше, чем благоприятнее для “человека”.

Это значение конечным вершинам дерева игры должно присваиваться с помощью некоторой оценочной функции (оценка(s_i)).

Разработка оценочной функции один из главных моментов в разработке игровой программы, так как от неё зависит качество хода компьютера.

Эти оценки распространяются вверх по дереву с помощью стратегии минимакса. Эта стратегия заключается в следующем. В качестве оценки для вершины соответствующей ходу “компьютера” алгоритм выбирает максимальное значение из оценок сыновей этой вершины. Для вершины “человека” алгоритм выбирает минимальное значение из оценок сыновей. Начиная с конечных вершин, последовательно обеспечивается минимум или максимум на более высоком уровне дерева. Процесс заканчивается присвоением значения оценки корню дерева. Значение, присвоенное корню дерева, считается лучшим, и этот ход выбирается алгоритмом. Выглядит это следующим образом. В этом случае выбирается один из ходов с жирной чертой.

АЛЬФА-БЕТТА ПРОЦЕДУРА

Возможно существенное улучшение алгоритма поиска лучшего хода, которое называется (α-β) процедура. Принцип состоит в следующем: двигаясь “сначала вглубь”, предположим, что на произвольном уровне дерева мы получили ситуацию представленную на рис 2.

Рис. 2

Поскольку “человек” минимизирующий игрок, то в вершине B оценка будет – (-5). Затем исследуют вершины F, G, H, …. Вершина G позволяет обеспечить в вершине F предварительный минимум 6; вершина H позволяет заменить минимум, соответствующий в F, на (-8). Но рассмотрим вершину A, которую надо максимизировать. Предварительный максимум это значение вершины B, т.е. (-5). Другими словами, максимизирующий игрок в вершине A, наверняка будет иметь ход, обеспечивающий значение большее или равное (-5). В то же время, если выбран ход ведущий в F, то человек мог бы дать этой вершине значение, меньшее или равное (-8). Максимизирующий игрок (т.е. “компьютер”) никогда не выберет такого хода. Таким образом, отпадает необходимость в исследовании вершин I, J, …, P и построения поддеревьев, имеющих эти вершины в качестве корней.

Следовательно, происходит выигрыш по времени, который в зависимости от ситуации может быт очень значительным.

ЗАДАНИЯ К КУРСОВЫМ РАБОТАМ

1. Шахматная N – ходовка с участием пешек, ферзей и слонов.

2. Шахматная N – ходовка с участием пешек, ладей и коней.

3. Шахматная N – ходовка с участием пешек, ферзей и коней.

4. Шахматная N – ходовка с участием пешек, ферзей и ладей.

5. Шахматная N – ходовка с участием пешек, ладей и слонов.

6. Шахматная N – ходовка с участием пешек, слонов и коней.

7. Написать программу играющую в ШАШКИ.

8. Написать программу играющую в ПОДДАВКИ.

9. Написать программу играющую в ГО

10. Написать программу играющую в ГЕКСАГОН.

Поле состоит из 6-гранных клеток. Размер поля – по выбору.

Два игрока ходят по очереди. Возможны ходы:

1) Поставить новую свою шашку на любую свободную из 6 клеток, смежных со своей шашкой.

2) Переставить свою шашку на любую свободную клетку, смежную с клетками, смежными с прежним положением этой шашки.

В любом случае, если на клетках, смежных с новым положением своей шашки, есть шашки противника, они заменяются на свои.

Игра заканчивается, когда все клетки заняты. Выигрывает тот, кто занял больше клеток.

11. Написать программу играющую в КВАДРАТЫ

12. Написать программу играющую в 5 ПОЛЕЙ

Поле n n клеток с четырёх сторон окружено такими же полями-лепестками. Играют два игрока. Вначале шашки одного игрока заполняют один лепесток, другого соседний. Игроки ходят по очереди. Возможные ходы.

1) Переставить свою клетку на соседнюю клетку.

2) Переставить свою шашку через соседнюю клетку, если та занята другой шашкой. За один ход можно последовательно перешагнуть через несколько шашек.

Выигрывает тот, кто быстрее переставит все свои шашки на противоположный лепесток.

13. Написать программу играющую в игру БОРЬБА ЗА ЖИЗНЬ

Два игрока имеют по n шашек и играют в поле m m клеток, делая ходы по очереди.

Возможные ходы:

1) переставить свою шашку на соседние свободные клетки

2) переставить свою шашку через поле, если оно занято другой шашкой.

Если шашка с трёх сторон окружена шашками противника, она снимается с поля. Если пустая клетка с 3-х сторон окружена шашками одного игрока, на её место ставится новая шашка этого игрока. Цель игры – убрать с доски все шашки противника.

14. Написать программу играющую в игру БЕГ В ЛАБИРИНТЕ

Игроки А и Б перемещаются внутри лабиринта. Игрок А на каждом шаге перемещается на одну позицию и имеет цель выйти из лабиринта. Игрок Б на каждом шаге либо перемещается на одну позицию, либо строит стенку на любой из соседних позиций. Игроки ходят по очереди. За игрока Б играет программа, имея целью помешать выход А из лабиринта.

15. Написать программу играющую в игру МЕЛЬНИЦА

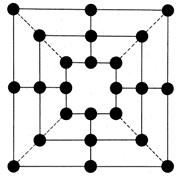
В начале игры оба играющих выставляют по очереди каждый свои 9 фишек на любые кружки игрового поля, стараясь поставить три фишки в один ряд. Задача играющего — расположить свои фишки на игровом поле так, чтобы партнёр не мог замкнуть ряда. После того как все 18 фишек будут выставлены, они начинают делать ходы, передвигаясь на один свободный кружок по чёрным линиям (сплошным или штриховым). Цель остаётся та же — построить три фишки в ряд по горизонтали, вертикали или диагонали.

Построив такой ряд, играющий снимает одну фишку противника. Построив второй, снимает ещё одну фишку и т.д. Разрешается “перепрыгивать” через одну фишку (свою или противника), если за нею имеется свободный кружок. Тот, у кого останутся две фишки, считается проигравшим, так как из двух фишек уже нельзя построить ряд.

Иногда применяется ещё одно дополнительное правило. Когда у одного играющего остаются всего три фишки, он получает право переносить свою фишку на любой кружок игрового поля, независимо от начерченных линий, тогда как второй играющий ходит по обычным правилам до тех пор, пока у него не останутся три фишки.

16. Написать программу играющую в игру ЧЕТЫРЕ В РЯД

Игра как в обычные крестики нолики, но собрать необходимо ряд из четырёх элементов.

17. Написать программу играющую в игру ОБРАТНЫЕ КРЕСТИКИ НОЛИКИ

Игра на доске крестиков – ноликов. Любой игрок может поставить крестик или нолик.

Один игрок стремится к появлению на доске любого ряда – крестиков или ноликов, другой ему препятствует. Первый выигрывает, если на доске появится ряд, и проиграет в противном случае.

18. Написать программу играющую в игру ПЯТЬ В РЯД 1

Игра как в обычные крестики нолики, но на бесконечном поле и собрать необходимо ряд из пятти элементов.

19. Написать программу играющую в игру ПЯТЬ В РЯД 2

В квадрате n n.

Крестик или нолик ставится либо на нижнюю сторону квадрата, либо на другой крестик или нолик.

20. Написать программу играющую в игру РЭНДЗЮ

21. Написать программу играющую в игру УГОЛКИ

Цель игры переставить шашки из своего угла (дома) в угол соперника раньше, чем он построит свои в Вашем углу. Ходы делаются поочереди. Движение возможно по горизонталям и вертикалям только в направлениях к углу противника. За один ход передвигается не более одной шашки. Шашка может либо передвигаться на одно поле либо перепрыгивать через одну или несколько шашек.

Игра заканчивается, когда один из игроков построил все свои шашки в доме противника. Все шашки необходимо вывести из своего дома не позднее чем за 3*'количество шашек' ходов - иначе будет засчитан проигрыш.

22. Написать программу играющую в игру МАНКАЛА

У каждого из двух партнеров по шесть коробочек-ниш, в каждой из которых три камня, но можно играть на доске 6х2, поля которой соответствуют нишам, а камни раскладываются прямо на полях.

Сбоку от доски имеются две большие ниши – манкалы. Правая от игрока – банк: попавшие туда камни становятся его собственностью. В начале игры во всех нишах по три камня. На каждом ходу игрок берет камни из своей ниши и раскладывает их по одному против часовой стрелки, включая свою манкалу, а манкалу противника пропускает. После хода игрока возможны четыре ситуации:

1) последний камень попал в его собственную нишу, причем она заполнена камнями. Тогда игрок продолжает ход, раскладывая все камни уже из этой ниши;

2) последний камень попал в его пустую нишу; тогда он забирает все камни из ниши соперника (если она не пуста), расположенной напротив, и помещает их в свою манкалу;

3) последний камень попал в манкалу; тогда он делает еще одну раскладку из любой своей ниши;

4) последний камень попал в нишу противника; тогда камни не берутся, а ход передается партнеру.

Игра завершается, когда все ниши одного из игроков окажутся пустыми. В этом случае соперник перекладывает оставшиеся камни в свою манкалу. Выигрывает тот, чья манкала содержит больше камней.

23. Написать программу играющую в игру КАЛАХ

Играют двое, ходы выполняются по очереди. Камни по лункам разложены так, как показано на рисунке. Каждому игроку принадлежит ближний ряд лунок и правый калах. Цель игры — накопить в своем калахе как можно больше камней. Игрок берет камни из любой лунки своего ряда и раскладывает их против часовой стрелки по одному в лунки своего ряда, затем в свой калах, пропуская калах противника, затем в лунки ряда противника.

Правила. Ход закончен, когда положен последний камень. Если ход закончен в своем калахе, игрок получает право на дополнительный ход. Иногда получаются замечательные каскады дополнительных ходов. Если ход заканчивается в своей пустой лунке, то игрок берет все камни из противоположной лунки ряда партнера и свой камень, и кладет в свой калах. Когда все лунки ряда одного из игроков окажутся пустыми и ему нечем совершать очередной ход, игра заканчивается. Тогда второй игрок переносит все камни из своего ряда в калах. Выигрывает тот, кто собрал в калахе больше половины всех камней. При равенстве количества камней в калахах партия считается ничейной.

24. Написать программу играющую в игру ЧИСОЛО

Здесь у игроков по два ряда лунок, причем в каждой по семь камней (игра как бы ведется на доске 7х4). Начальная расстановка показана на рисунке.

Партнеры раскладывают камни только по двум рядам своих лунок (большие лунке не участвуют в процессе, а в них собираются снятые камни) по часовой стрелке или против. При раскладке возможны три варианта:

1) если последний камень попал в лунке, в которой есть камни, то ход не заканчивается: игрок забирает их и продолжает раскладывать дальше;

2) если последний камень попал в пустую лунку первого ряда (ближнего к игроку), то ход передается сопернику;

3) если последний камень попал в пустую лунку второго ряда (ближнего к партнеру), то игрок забирает в свою большую лунку все его камни из двух лунок напротив и, кроме того, еще из одной любой лунки соперника (если обе лунки напротив пусты, то из третьей камни не берутся).

Выигрывает тот, кто первым захватит все камни соперника.

25. Написать программу играющую в игру НИМ

Вначале фишки раскладываются на несколько рядов. Игроки по очереди забирают одну или несколько фишек из любого ряда. Не разрешается за один ход брать фишки из нескольких рядов. Выигрывает тот, кто возьмет последнюю фишку (фишки).

26. Написать программу играющую в игру ОТЕЛЛО (РЕВЕРСИ)

27. Написать программу играющую в игру ТАК-ТИКС

На доске n n расставлены одинаковые фишки, на каждом поле по одной. Игроки по очереди берут несколько фишек из одного вертикального, горизонтального ряда или части ряда не содержащего дырок. Проигрывает тот, кто вынужден взять последнюю фишку.

28. Написать программу играющую в игру БРИДЖ-ИТ

Игра в квадрате n n. Партнёры по очереди проводят горизонтальные и вертикальные отрезки, соединяя ими точки своего цвета. Линии противников нигде не должны пересекатся. Выигрывает тот кто первым построит ломаную своего цвета, связывающую потивоположные стороны доски.

29. Написать программу играющую в игру РАССАДА

Вначале рисуется несколько точек. Каждым ходом игрок может или нарисовать петлю из какой либо точки, или соединить две точки кривой, при этом на этой петле или кривой рисуется новая точка. Нельзя пересекать линии и точки. Из одной точки не должно быть более трех линий ("ростков"). Кто не сможет сделать очередного хода, тот проиграл.

30. Написать программу играющую в игру ОУА

31. Написать программу играющую в игру ПОЛИЦЕЙСКАЯ МАШИНА

Погоня происходит на бесконечном поле. У одного “полицейская машина”, у другого – “машина преступников”. Игроки ходят по очереди: по горизонтали или вертикали. Машина преступников перемещается на одну клетку, а полицейская на две. Однако блюстителям порядка запрещены левые повороты и развороты. Они могут двигаться либо прямо в направлении стрелки, либо направо.

32. Написать программу играющую в игру ПОЛЗУНОК

Игровое поле представляет собой решётку (обычно размерами 5 на 6 точек).

Играют двое, проводя по очереди горизонтальные или вертикальные “единичные” отрезки. Требуется, чтобы получающаяся траектория игры была непрерывной, однако присоединять новый отрезок к уже имеющейся ломаной можно с любого конца. Проигрывает тот, кто вынужден своим ходом замкнуть траекторию. Но, например, в нижней позиции тот, чья очередь ходить, также проигрывает.