Вариант 17
Найти область сходимости и расходимости степенного ряда.
Разложить функцию по степеням до третьего слагаемого с остаточным членом в форме Пеано:
Разложить функцию в степенной ряд с центром в точке пользуясь известными стандартными разложениями в ряд Тейлора. Определить интервал сходимости.
а)
б)
С помощью разложения функции в степенной ряд вычислить ее приближенное значение в точке с заданной точностью
С помощью разложения функции в степенной ряд вычислить приближенное значение интеграла с заданной точностью
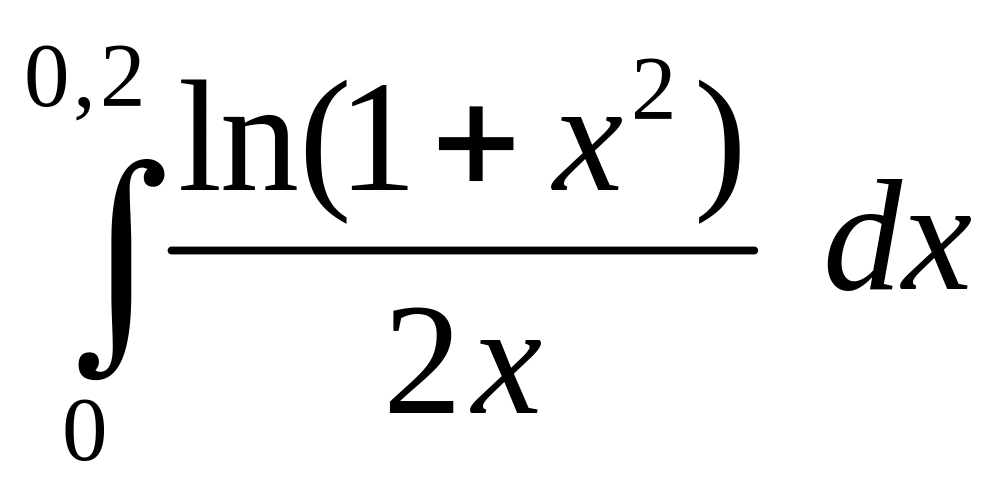с точностью
На промежутке аппроксимировать функцию многочленом Тейлора с центром в нуле.
Построить в одной системе координат графики и .
Вычислить погрешность аппроксимации в точках
Подобрать такоe значение чтобы многочлен Тейлора аппроксимировал функцию с точностью во всех точках промежутка
Вычисления и построение графиков следует проводить в одном из математических пакетов (например, в Maple).
Вариант 18
Найти область сходимости и расходимости степенного ряда.
Разложить функцию по степеням до третьего слагаемого с остаточным членом в форме Пеано:
Разложить функцию в степенной ряд с центром в точке пользуясь известными стандартными разложениями в ряд Тейлора. Определить интервал сходимости.
а)
б)
С помощью разложения функции в степенной ряд вычислить ее приближенное значение в точке с заданной точностью
С помощью разложения функции в степенной ряд вычислить приближенное значение интеграла с заданной точностью
с точностью
На промежутке аппроксимировать функцию многочленом Тейлора с центром в нуле.
Построить в одной системе координат графики и .
Вычислить погрешность аппроксимации в точках
Подобрать такоe значение чтобы многочлен Тейлора аппроксимировал функцию с точностью во всех точках промежутка
Вычисления и построение графиков следует проводить в одном из математических пакетов (например, в Maple).
Вариант 19
Найти область сходимости и расходимости степенного ряда.
Разложить функцию по степеням до третьего слагаемого с остаточным членом в форме Пеано:
Разложить функцию в степенной ряд с центром в точке пользуясь известными стандартными разложениями в ряд Тейлора. Определить интервал сходимости.
а)
б)
С помощью разложения функции в степенной ряд вычислить ее приближенное значение в точке с заданной точностью
С помощью разложения функции в степенной ряд вычислить приближенное значение интеграла с заданной точностью
с точностью
На промежутке аппроксимировать функцию многочленом Тейлора с центром в нуле.
Построить в одной системе координат графики и .
Вычислить погрешность аппроксимации в точках
Подобрать такоe значение чтобы многочлен Тейлора аппроксимировал функцию с точностью во всех точках промежутка
Вычисления и построение графиков следует проводить в одном из математических пакетов (например, в Maple).
