ДОМАШНЯЯ КОНТРОЛЬНАЯ РАБОТА
ПО ТЕМЕ
“Степенные ряды ”
Общие требования к оформлению:
переписывать условия заданий
пояснять ключевые действия словами
все утверждения о сходимости или расходимости тех или иных числовых рядов обосновывать ссылкой на признаки сходимости
в задачах 1-5 писать ответ
Количество баллов за задачи (всего 22):
1 – 2 балла
2 – 2 балла
3 – 2 балла за каждый пункт
4 – 3 балла
5 – 4 балла
6 – 7 баллов
ВАРИАНТ 1
Найти область сходимости и расходимости степенного ряда.
Разложить функцию
по степеням
до третьего слагаемого с остаточным
членом в форме Пеано:
Разложить функцию в степенной ряд с центром в точке
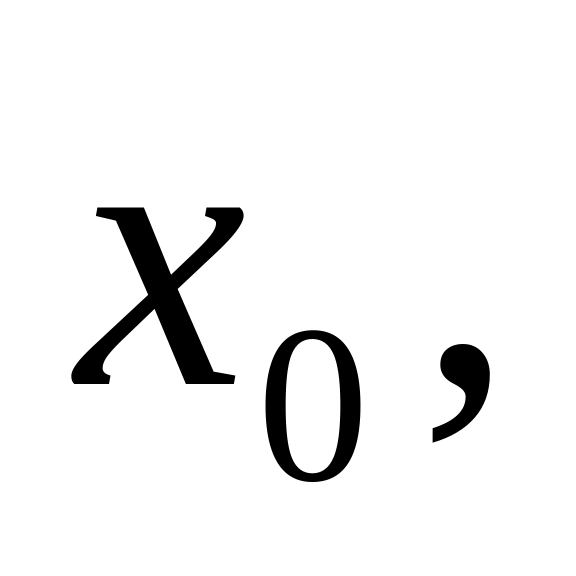пользуясь известными стандартными
разложениями в ряд Тейлора. Определить
интервал сходимости.
а)
б)
С помощью разложения функции в степенной ряд вычислить ее приближенное значение в точке
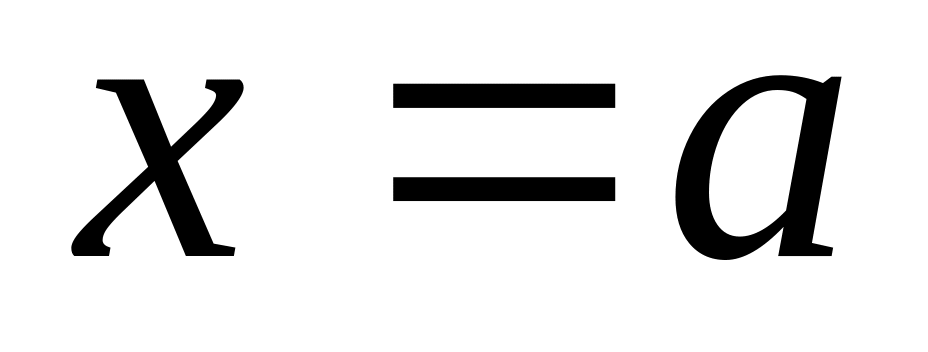с заданной точностью
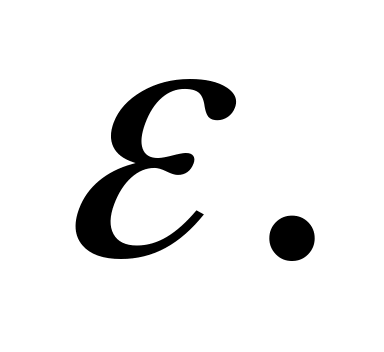
С помощью разложения функции в степенной ряд вычислить приближенное значение интеграла с заданной точностью
На промежутке
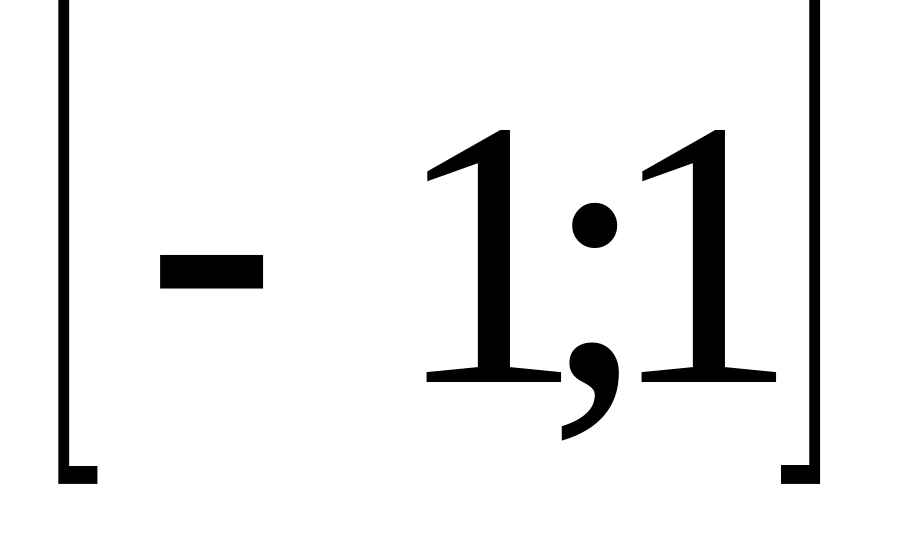аппроксимировать функцию
многочленом Тейлора
с центром в нуле.
Построить в одной системе координат графики и .
Вычислить погрешность аппроксимации в точках
Подобрать такоe значение
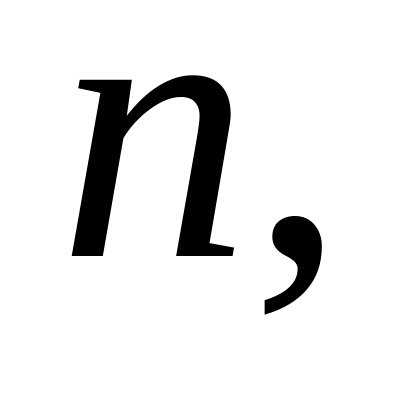чтобы многочлен Тейлора
аппроксимировал функцию
с точностью
во всех точках промежутка
Вычисления и построение графиков следует проводить в одном из математических пакетов (например, в Maple).
Вариант 2
Найти область сходимости и расходимости степенного ряда.
Разложить функцию по степеням до третьего слагаемого с остаточным членом в форме Пеано:
Разложить функцию в степенной ряд с центром в точке пользуясь известными стандартными разложениями в ряд Тейлора. Определить интервал сходимости.
а)
б)
С помощью разложения функции в степенной ряд вычислить ее приближенное значение в точке с заданной точностью
С помощью разложения функции в степенной ряд вычислить приближенное значение интеграла с заданной точностью
На промежутке аппроксимировать функцию многочленом Тейлора с центром в нуле.
Построить в одной системе координат графики и .
Вычислить погрешность аппроксимации в точках
Подобрать такоe значение чтобы многочлен Тейлора аппроксимировал функцию с точностью во всех точках промежутка
Вычисления и построение графиков следует проводить в одном из математических пакетов (например, в Maple).
Вариант 3
Найти область сходимости и расходимости степенного ряда.
Разложить функцию по степеням до третьего слагаемого с остаточным членом в форме Пеано:
Разложить функцию в степенной ряд с центром в точке пользуясь известными стандартными разложениями в ряд Тейлора. Определить интервал сходимости.
а)
б)
С помощью разложения функции в степенной ряд вычислить ее приближенное значение в точке с заданной точностью
С помощью разложения функции в степенной ряд вычислить приближенное значение интеграла с заданной точностью
На промежутке аппроксимировать функцию многочленом Тейлора с центром в нуле.
Построить в одной системе координат графики и .
Вычислить погрешность аппроксимации в точках
Подобрать такоe значение чтобы многочлен Тейлора аппроксимировал функцию с точностью во всех точках промежутка
Вычисления и построение графиков следует проводить в одном из математических пакетов (например, в Maple).
Вариант 4
Найти область сходимости и расходимости степенного ряда.
Разложить функцию по степеням до третьего слагаемого с остаточным членом в форме Пеано:
Разложить функцию в степенной ряд с центром в точке пользуясь известными стандартными разложениями в ряд Тейлора. Определить интервал сходимости.
а)
б)
С помощью разложения функции в степенной ряд вычислить ее приближенное значение в точке с заданной точностью
С помощью разложения функции в степенной ряд вычислить приближенное значение интеграла с заданной точностью
На промежутке аппроксимировать функцию многочленом Тейлора с центром в нуле.
Построить в одной системе координат графики и .
Вычислить погрешность аппроксимации в точках
Подобрать такоe значение чтобы многочлен Тейлора аппроксимировал функцию с точностью во всех точках промежутка
Вычисления и построение графиков следует проводить в одном из математических пакетов (например, в Maple).
