5. Экспертные процедуры при выборе оптимальных вариантов решений

В практических задачах принятия решений характеристики сравниваемых альтернатив не всегда могут быть измерены. В этих случаях для количественной оценки соответствия свойств альтернативных вариантов предъявляемым требованиям приходится решать задачи экспертного оценивания, суть которых в том, что специалисты в рассматриваемой предметной области осуществляют относительное численное ранжирование сравниваемых свойств альтернативных вариантов решения.

Специалисты, привлекаемые для количественного сравнительного оценивания альтернатив, называются экспертами, а процесс решения задач оценивания – экспертизой.

Для повышения достоверности и надежности результатов оценивания обычно в экспертизе участвует группа специалистов (групповая экспертиза).

Индивидуальные экспертные оценки имеют случайный характер в связи с тем, что на их численные значения оказывают влияние знания и опыт каждого специалиста, их самочувствие, настроение и окружающая обстановка, поэтому при групповой экспертизе необходимо формировать усредненную упорядоченность, которая должна максимально приближаться к истинному значению оценки.

В результате групповой экспертизы получается набор численных значений х_i, тогда для нахождения среднего значения оценки используется соотношение:

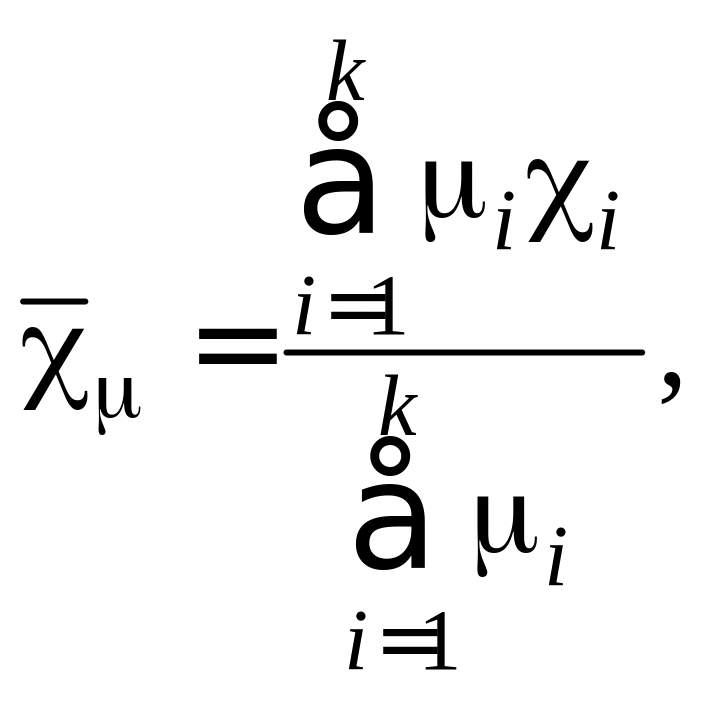
где k – число экспертов в группе, _i – коэффициент авторитета i-го эксперта.

Среднее значение оценки х_i выражает коллективное мнение группы экспертов, причем степень среднеквадратического разброса оценок х_i отдельных экспертов обычно характеризуется величиной называемой дисперсией экспертных оценок, где  – среднеквадратическая оценка.

Надежность экспертизы тем выше, чем меньшую долю среднего значения составляет среднеквадратический разброс оценок или их вариация:

Для определения интервального значения групповой экспертной оценки вводится понятие доверительного интервала , для определения которого при известном количестве экспертов «k» задается величина доверительной вероятности «р»:

где  – коэффициент Стьюдента, определяемый по таблицам как функция двух аргументов (р и k).

После определения с вероятностью «р» можно утверждать, что истинное значение оценки х_i лежит в пределах интервала, ограниченного с вероятностью «р».

Для определения необходимого количества экспертов в группе можно преобразовать соотношение, которое применяется при расчете величины доверительного интервала:

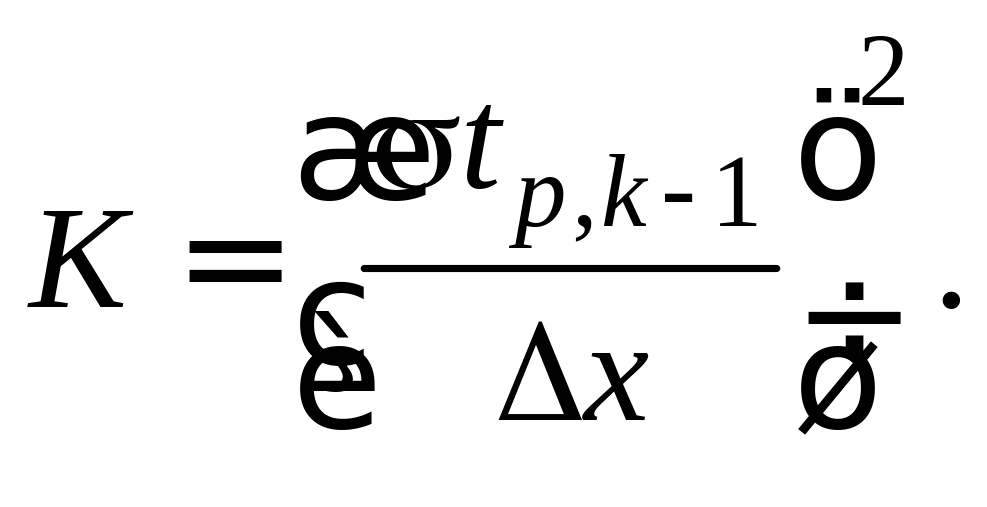
Если использовать выражение «вариации» и ввести понятие относительной ширины доверительного интервала можно получить формулу для определения числа экспертов в группе:

При расчете численного состава группы экспертов априорное значение вариации выбирается в пределах (0,2 : 0,3), относительная ширина доверительного интервала  = 0,1 и доверительная вероятность р = (0,8 : 0,9). Для нахождения по таблице коэффициента Стьюдента t задается начальное значение K₀ = 10.

Коэффициент авторитета i-го эксперта _i, характеризующий степень его компетентности, представляется в нормализованной форме:

При определении численного значения _i исходным служит утверждение, что коллективное мнение группы специалистов примерно одинакового интеллектуального уровня и одинаковой опытности более соответствует истине, чем мнение одного представителя этой группы.

К величине коэффициента авторитета экспертов предъявляется ряд требований:

ограничение пределами (0,1);

монотонное изменение на интервале 0 и 1;

разность между х_i и , должна быть тем меньше, чем меньше дисперсия экспертных оценок данного эксперта

Учитывая приведенные требования и принцип формирования коллективного мнения группы экспертов, для расчета _i i-го эксперта предлагается формула:

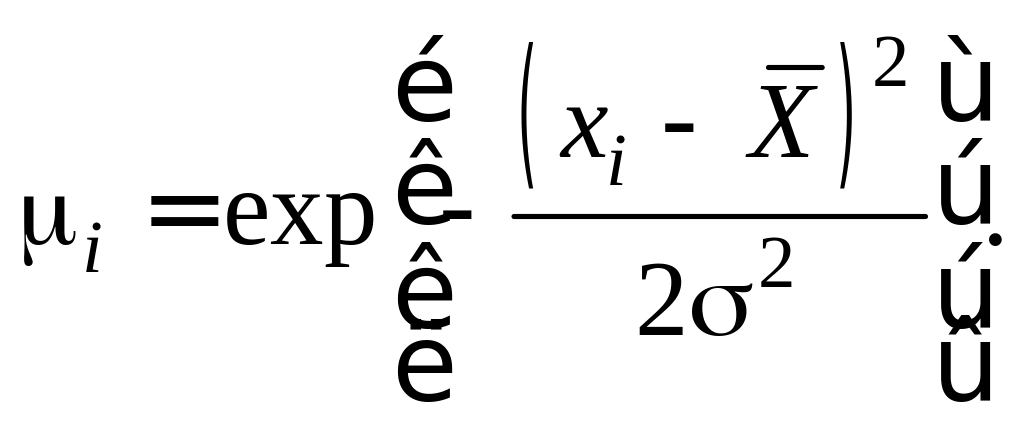
К специалистам, которые включаются в группу экспертов, предъявляется ряд требований:

1) должны обладать запасом необходимых фундаментальных знаний, позволяющих на основе наблюдения создавать модель анализируемого объекта (явления), с помощью которой можно получить количественные оценки его свойств;

2) область практической деятельности эксперта должна совпадать с той специализацией, к которой относится исследуемый объект;

3) оценки эксперта должны быть стабильны во времени и транзистивны, т. е. должны обладать свойством общности для выбранных объектов, представляющих некоторую совокупность;

4) оценки экспертов должны обладать тем свойством, что получение дополнительных объективных сведений об исследуемых объектах приводит к повышению достоверности этих оценок.

Для выявления кандидатов в группу экспертов при оценивании конкретных объектов предлагается проанализировать список литературы, приведенный в трех и более монографиях, посвященных рассматриваемой области науки и техники. Из списка выбрать фамилии авторов, имеющих не менее трех публикаций в этой области. К ним обратиться с просьбой назвать не менее десяти наиболее авторитетных специалистов, работающих в данной области. Из полученных списков (множеств) найти их пересечения, т. е. выбрать фамилии специалистов, которые встречаются в десяти списках не менее семи раз. Эти специалисты проверяются на соответствие требованиям, которые приведены выше.