4. Математические модели и алгоритмы выбора оптимальных вариантов структуры и вектора варьируемых параметров относительно бкп и укп при системном проектировании

Наше знание всегда относительно, поэтому любое описание на любом языке также отображает лишь некоторые стороны явлений и никогда не является абсолютно полным.

Употребляя слово «модель», «модельное описание», нужно иметь в виду некоторое описание, отражающее именно те особенности изучаемого процесса, которые интересуют исследователя.

Если при описании моделей используется язык математики, то имеются в виду математические модели.

Построение математических моделей является основой всего системного анализа, т. е. это центральный этап исследования или проектирования любой системы.

Модель должна достаточно правильно отражать исследуемые явления, однако одного этого еще мало. Она должна быть удобной для использования, поэтому степень детализации модели, форма ее представления и т. д. определяются целями исследования и непосредственно зависят от исследователя.

Проблема математического моделирования состоит в описании принципов отбора в терминах и переменных, которые согласно взглядам исследователя наиболее полно характеризуют изучаемый предмет.

Построением и анализом математических моделей процессов многокритериального выбора оптимальных решений занимается теория выбора и принятия решений.

Согласно теории выбора вводятся упрощающие допущения, которые принимаются при построении математических моделей процедур многокритериального выбора оптимального варианта структуры проектируемой системы и определении оптимальных значений ее параметров:

* формируемые множества альтернативных вариантов структуры и вектора варьируемых параметров системы считаются полными в том смысле, что они содержат оптимальный вариант (в понимании – лучший из сравниваемых);

* показатели качества количественно характеризуют степень соответствия отдельных свойств альтернативных вариантов проектируемой системы предъявляемым к ней требованиям вне зависимости от наличия связей между характеристиками этих свойств (объем, масса и др.);

* с помощью уточнения ограничений, накладываемых на структуру, показатели качества и параметры проектируемой системы можно расширять или сужать множество альтернативных вариантов, которые близки к оптимальному, для обеспечения условий реализуемости выбранного оптимального варианта при заданном окружении (выбирается лучший из реально реализуемых).

Выбор оптимального решения при системном проектировании основан на процедурах системного анализа: «…выдвижение альтернативных вариантов решения проблемы, выявление масштабов неопределенности по каждому из вариантов…».

Соответственно, математическая модель процедур выбора должна включать два множества: множество альтернативных вариантов и множество характеристик свойств альтернативных вариантов. Формирование указанных множеств является необходимым, но не достаточным условием однозначного выбора оптимального решения, так как абсолютного оптимального варианта, не зависящего от окружающих условий, не существует.

Для выполнения условия достаточности однозначного многокритериального выбора оптимального решения формируется еще одно множество – множество ограничений, учитывающих связи моделируемого объекта с окружающей средой (У) и внешними объектами «О_к», «О_s» и «О_п».

Завершается выбор сопоставлением альтернативных вариантов с помощью принятого критерия предпочтения. Соответственно элементами математической модели процедур многокритериального выбора являются три множества и правило (принцип) выбора одного компромиссного решения [6].

Математическая модель процедур многокритериального выбора S_opt :

• множество альтернативных вариантов структур проектируемой системы, которые обеспечивают достижение многомерной цели ее функционирования при заданном окружении M(S) = (S_i: обеспечивает выполнение требований при «У»), где У – совокупность внешних условий;

• множество показателей качества, позволяющих количественно оценивать степень соответствия свойств альтернативных вариантов структуры предъявляемым требованиям: K(S_i) = K_1i, K_2i, …, K_mi.

• множество ограничений, накладываемых на структуру «О_s» и на показатели качества «О_к»:

О_s = (О_si: отражают внешние структурные связи проектируемой системы),

О_к = (О_кi: отражают внешние функциональные связи проектируемой системы);

• правило выбора оптимального, в смысле компромиссного, варианта структуры

,

при

Принцип формирования укп на языке «функций выбора» при структурной оптимизации основан на принципе системной иерархии: рассматривается система более высокого уровня иерархии по отношению к проектируемой, и выделяется ее доминирующее свойство. Из оптимальных относительно БКП нехудших вариантов проектируемой системы выбирается такой, у которого ПК «выделенного свойства» К_i имеет наименьшее значение, и соответственно показатель степени _i функции значимости должен иметь наибольшую величину (из остальных α_j) при К_i ≤ 1.

Математическая модель процедур многокритериального выбора оптимального вектора варьируемых параметров Х_opt:

* множество ЦФ, представляемых в виде аналитических зависимостей ПК от x_i:

* множество ограничений, накладываемых на варьируемые параметры О_п = (О_пi: отражают внутренние функциональные связи проектируемой системы);

* множество допустимых альтернативных вариантов вектора варьируемых параметров М_д(Х) = (Х_i: удовлетворяют ограничениям «О_п») М_д(Х) = М(Х) \ М( _п);

* правило выбора оптимального, в смысле компромиссного, варианта вектора Х:

при

Принцип формирования УКП на языке «функции выбора» при параметрической оптимизации основан на принципе наибольшего приближения компромиссного варианта Х к идеальному, для которого целевые функции равны нулю:

Величина приближения Х_расч к Х_ид определяется как среднеквадратическое значение

Анализ свойств построенных математических моделей:

* модели универсальны, т. е. могут быть использованы при проектировании систем любой физической природы при условии, что эти системы описываются на структурном уровне численными значениями ПК, а на параметрическом уровне – численными значениями ЦФ (целевых функций);

* не все процедуры математических моделей могут быть формализованы. Выбор характеристик свойств альтернативных вариантов проектируемой системы, используемых для оценки степени соответствия этих свойств, предъявляемым функциональным требованиям (ПК) , а также ограничений, накладываемых на структуру, показатели качества и варьируемые параметры, осуществляются с использованием знаний проектировщика, а поэтому не формализуются.

После построения модели оптимизации структуры и вектора варьируемых параметров проектируемой системы разрабатываются соответствующие алгоритмы.

Под АЛГОРИТМОМ будем понимать точное предписание относительной последовательности элементарных действий, преобразующих конкретные исходные данные в искомый результат. Алгоритмы можно представлять в виде логических блок-схем, на которых различаются операторы ввода и вывода – изображаются овалом с одним входом (ввод) и одним выходом (вывод результата). Арифметические операторы – в виде прямоугольников с большой буквой «А» и соответствующим индексом.

Операторы управления также в виде прямоугольников, но с другой буквой, например «кси» с соответствующим индексом. Счетчики выполненных операций – в виде прямоугольников с буквой «С» и индексом. Логические операторы (предикаты) – в виде ромбов. Арифметические операторы и операторы управления (счетчики) имеют один вход и один выход, а логические операторы – один вход и два выхода: по стрелке «1», когда проверяемое условие выполняется, и по стрелке «0», когда оно не выполняется.

Обозначим алгоритмы: Ал-1 выбора вариантов структуры и вектора Х, оптимальных относительно БКП; алгоритмы АЛ-2 и АЛ-3 выбора вариантов структуры и вектора Х, оптимальных относительно УКП.

Операторы Ал-1 реализуют процедуры бинарных отношений в виде сравнения численных значений ПК пар альтернативных вариантов структур или численных значений ЦФ пар альтернативных вариантов вектора Х из множества тех вариантов, которые близки к оптимальному:

Исходные данные АЛ-1:

матрица качества, т. е. таблица численных значений ПК альтернативных вариантов структуры или численных значений ЦФ альтернативных вариантов вектора варьируемых параметров Х из М_бо;

начальные значения индексов управления i₀ = 0, α₀ = 0, β₀ = 1.

Операторы Ал-2 реализуют процедуры расчета численных значений УКП при структурной оптимизации в виде произведения функций значимости где  – численные значения ПК.

Операторы Ал-3 при параметрической оптимизации в виде оценки среднеквадратического отклонения реальных вариантов вектора Х_нх от идеального варианта, имеющего К₁(Х_ид) = К₂(Х_ид) = … = К_m(Х_ид) = 0:

где К₁(Х_i), K₂(X_i), …, К_m(X_i) – численные значения ЦФ.

Исходные данные Ал-2:

матрица качества нехудших вариантов структуры проектируемой системы в виде таблицы численных значений их ПК;

численные значения показателей степени функций значимости α₁, α₂, …;

max величина значения УКП при К₁ = К₂ = … = К_m = 1, равная 1;

начальное значение индекса управления i₀ = 0.

Исходные данные Ал-3:

матрица качества нехудших вариантов вектора Х в виде таблицы численных значений их ЦФ;

max величина значения УКП при К₁(Х) = К₂(Х)= … = К_m(Х) = 1, равная ;

начальное значение индекса управления i₀ = 0.

Существуют различные формы записи алгоритмов.

В качестве примера приводятся символьно-логические формы записи АЛ-2, АЛ-3.

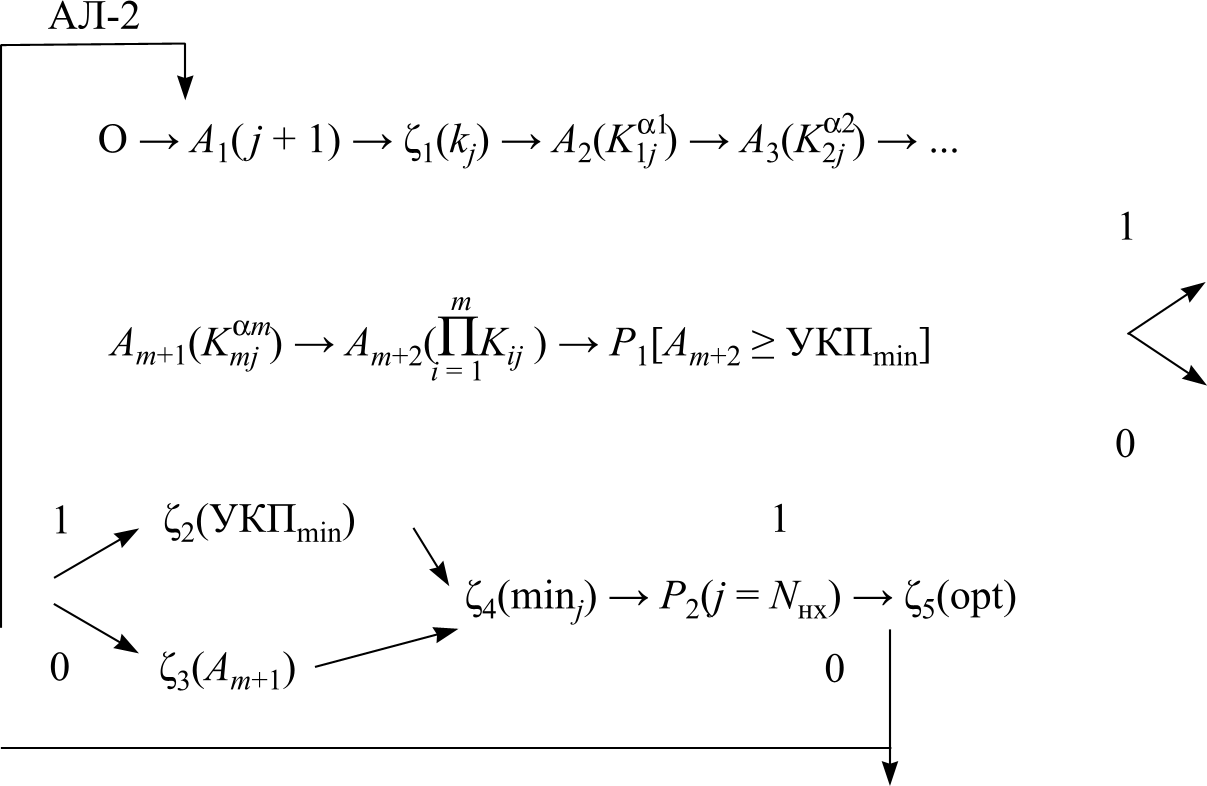
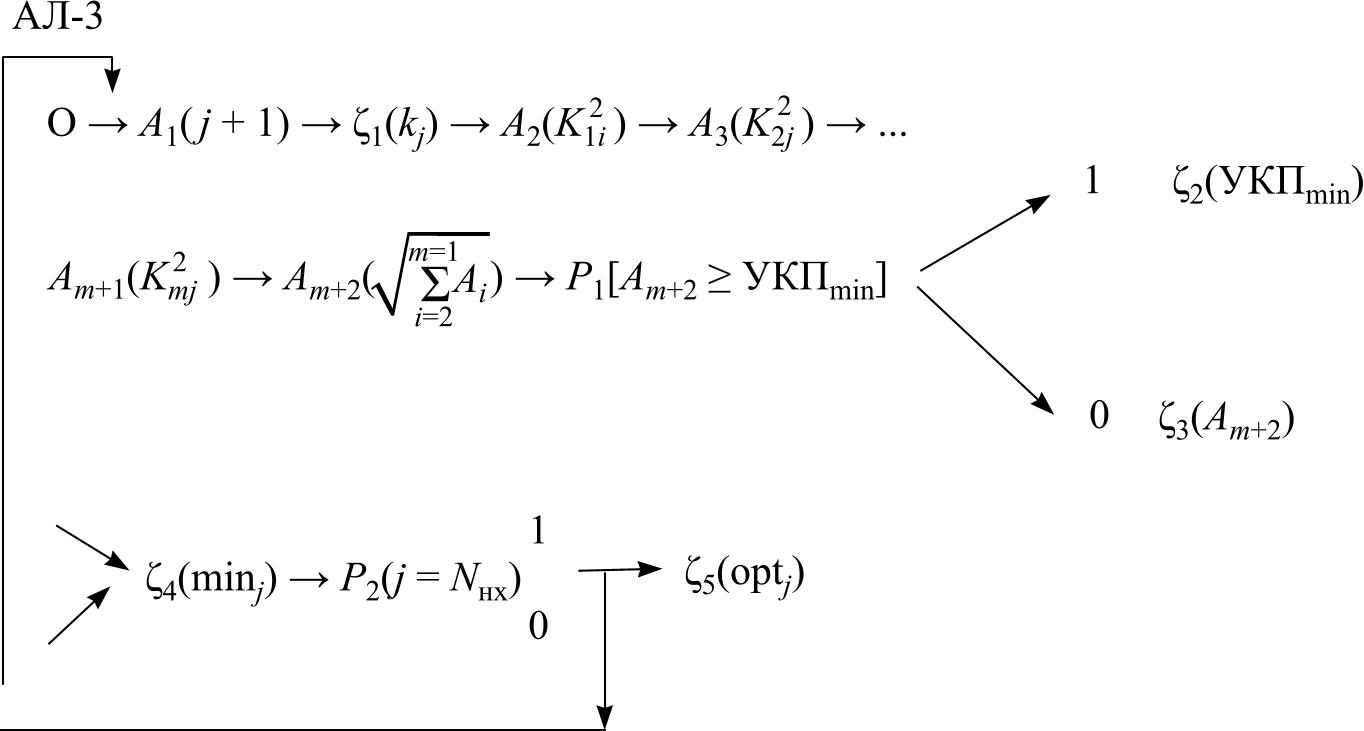
Алгоритмы АЛ-1, АЛ-2 и АЛ-3 универсальны в том смысле, что они применимы при проектировании любых систем, для которых могут быть получены матрицы качества.

Алгоритмы, описанные на языке, понятном ЭВМ, превращаются в машинные программы. Программы перечисленных алгоритмов АЛ-1, АЛ-2 и АЛ-3 использовались при разработке комплекса прикладных программ «Векторная оптимизация структуры и параметров систем вторичного электропитания радиоэлектронной аппаратуры».

Программы многокритериального выбора оптимальных вариантов структуры и вектора варьируемых параметров проблемно-ориентированы, так как включают процедуры расчета численных значений ПК и ЦФ, которые зависят не от свойств объекта, т. е. являются универсальными.

Методика многокритериальной структурной оптимизации технических систем получила аккредитацию на государственном уровне.