4. Решение задачи коммивояжера методом взвешенного графа
Для уяснения способа задания бинарных отношений с помощью взвешенного графа и его использования вместо комбинаторного программирования предлагается построить взвешенный граф для исходных данных, которые рассматривались в задаче коммивояжера (табл. 3.1).
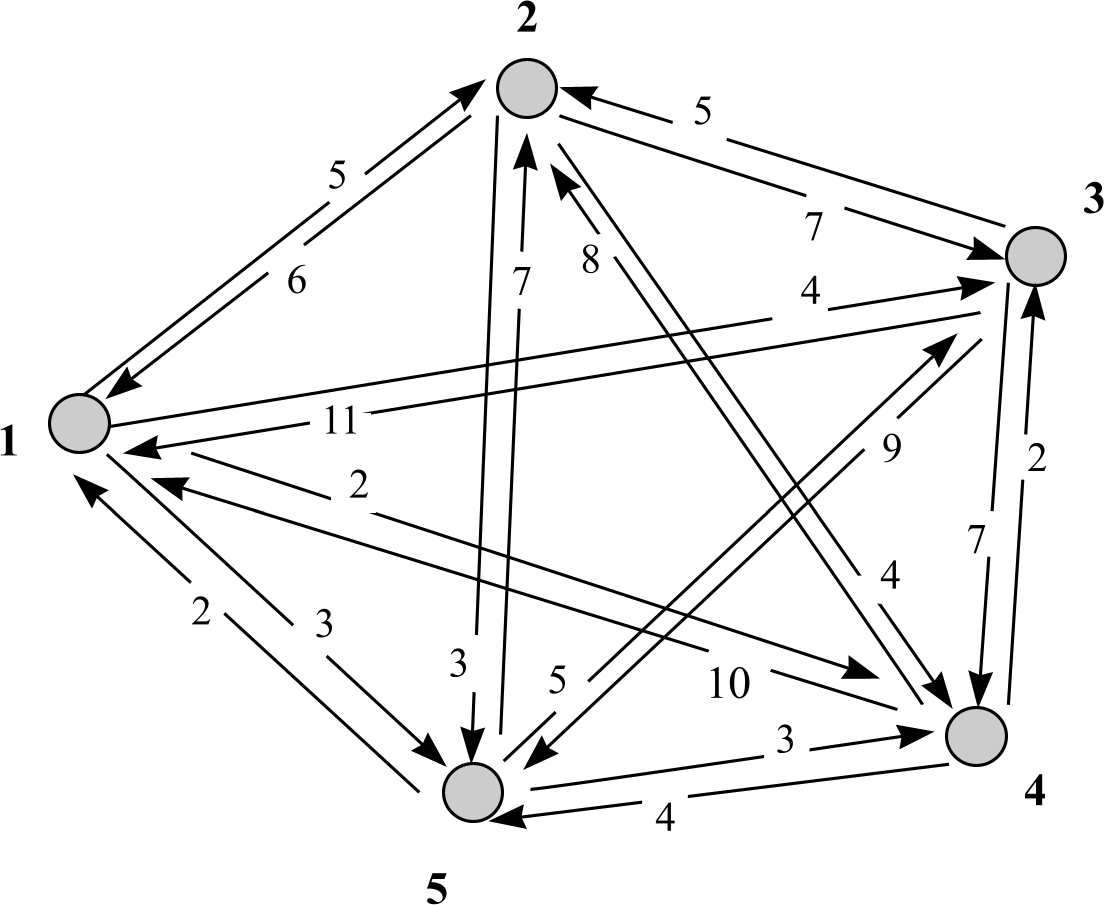
Рис. 4.1. «Взвешенный» граф
Преподаватель разъясняет студентам группы терминологию и принцип построения взвешенного графа, после чего студенты поочерёдно на доске строят граф (рис. 4.1) и представляют его в виде табл. 4.1, в которой:
1-я строка – исходящие из вершин li
и входящие
в вершины дуг взвешенного графа;
2-я строка – вершины графа, из которых дуги выходят V;
3-я строка – вершины графа, в которые дуги входят V;
4-я строка – «вес» дуги.
Таблица 4.1
Дуги |
l1 |
l1’ |
l2 |
l 2’ |
l 3 |
l 3 ι |
l 4 |
l 4 ι |
Вершины V |
1 |
2 |
1 |
3 |
1 |
4 |
1 |
5 |
Вершины V |
2 |
1 |
3 |
1 |
4 |
1 |
5 |
1 |
«Вес» дуги |
5 |
6 |
4 |
11 |
2 |
10 |
3 |
2 |
Дуги |
l 5 |
l 5’ |
l 6 |
l 6’ |
l 7 |
l 7’ |
Вершины V |
2 |
3 |
2 |
4 |
2 |
5 |
Вершины V |
3 |
2 |
4 |
2 |
5 |
2 |
«Вес» дуги |
7 |
5 |
4 |
8 |
3 |
7 |
Дуги |
l 8 |
l 8 ι |
l 9 |
l 9 ι |
Вершины V |
3 |
4 |
3 |
5 |
Вершины V |
4 |
3 |
5 |
3 |
«Вес» дуги |
7 |
2 |
9 |
5 |
Дуги |
l 10 |
l 10 ι |
Вершины V |
4 |
5 |
Вершины V |
5 |
4 |
«Вес» дуги |
4 |
3 |
Затем под руководством преподавателя студенты с места, а один из студентов у доски, анализируют построенную таблицу, представляющую граф, и последовательно выбирают дуги графа, имеющие наименьший «вес».
Сформированный оптимальный маршрут, имеющий вес 14 (min)
«Вес» = 2 + 2 + 5 + 3 + 2 = 14 (min)
5. Решение задачи однокритериальной оптимизации методом «покоординатного спуска»
Уяснение особенностей использования метода покоординатного спуска при линейном программировании (ЛП), достоинств и недостатков ЛП проводится на примере решения задачи однокритериальной многомерной оптимизации для случая трех целевых функций и двух ограничений, удовлетворяющих канонической форме записи.
Условия задачи лп
Целевые функции: |
Ограничения: |
К1(Х) = – 3х1 + 2х2 |
–2х1 – 3х2 + 18 0 |
К2(Х) = 4х1 + 3х2 |
–2х1 – х2 + 10 0 |
К3(Х) = – 2х1 + 5х2 |
х1 0; х2 0 |
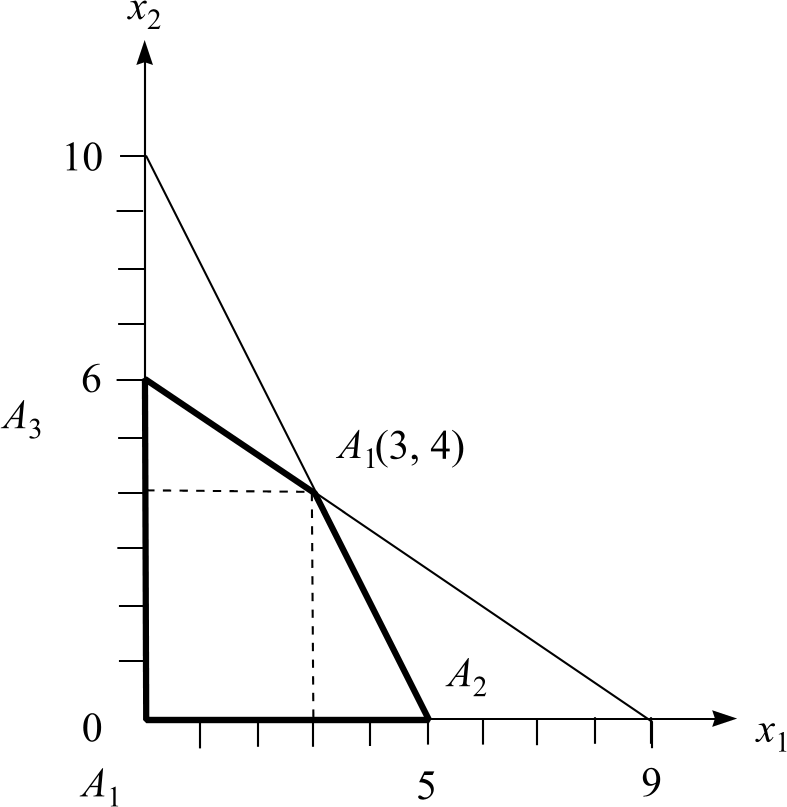
Преподаватель разъясняет студентам процедуру построения многогранника ограничений (рис. 5.1). Один из студентов на доске строит многогранник ограничений в системе координат (х1, х2) и фиксирует координаты его вершин, исключая вершину А1 с координатами (0, 0): А2(5, 0); А3(3, 4); А4(0, 6):
|
из –2х1 – 3х2 – 18 = 0
при х1 = 0 х2 = 6: точка (0, 6) при х2 = 0 х1 = 9: точка (9, 0)
из –2х1 –х2 – 10 = 0
при х1 = 0 х2 = 10: точка (0, 10) при х2 = 0 х1 = 5: точка (5, 0) |
Рис. 5.1. Построение многогранника ограничений |
|
Второй студент подставляет вершины А2, А3 и А4 в целевые функции и вычисляет оптимальный план каждой целевой функции. Присутствующие студенты убеждаются, что нет вершины, доставляющей максимум всем трем целевым функциям одновременно.
Преподаватель ставит перед студентами задачу поиска таких значений аргументов (х1, х2), которые обеспечивают компромиссное решение, а именно: посредством минимизации суммы квадратов разностей K(X)max, которые соответствуют оптимальным планам целевых функций с их общими выражениями, обеспечить максимальное приближение K1(X), K2(X), K3(X) к их максимальным значениям:
В полученное выражение подставляются значения K1(X)max = 12, K2(X)max = 24, K3(X)max = 10 и после раскрытия скобок студенты решают задачу отыскания минимума функции
в пределах допустимых значений аргументов (х1, х2), используя метод покоординатного спуска.
Студенты у доски по очереди выполняют процедуру поиска оптимального варианта значений аргументов, принимая как исходные координаты вершины А3 (х10 = 3; х20 = 4).
Оптимизируемые параметры принимают значения: х1 = 2,97; х2 =1,56.
Затем один из студентов подставляет оптимизированные значения х1 и х2 в целевые функции K1(X), K2(X), K3(X) и вычисляет их значения, которые рассматриваются как компромиссное решение.