3. Решение задачи коммивояжера
Для уяснения смыслового содержания
схемы последовательного анализа
вариантов рассмотрим процедуры,
применяемые при решении задачи
коммивояжера, который должен выбрать
маршрут посещения N городов,
обеспечивающий минимальное расходование
ресурсов. Расстояние (ресурс) между
городами i-м и j-м известно: Cij.
Общая длина «пути»
.
Коммивояжер возвращается в первый город (начало маршрута), посетив остальные города один раз.
Для формирования оптимального маршрута используется метод приведенных матриц.
У доски студенты решают задачу при N = 5 для исходных данных, приведенных в табл. 3.1.
Таблица 3.1
Города |
1 |
2 |
3 |
4 |
5 |
1 |
|
5 |
4 |
2 |
3 |
2 |
6 |
|
7 |
4 |
3 |
3 |
11 |
5 |
|
7 |
9 |
4 |
10 |
8 |
2 |
|
4 |
5 |
2 |
7 |
5 |
3 |
|
По окончании решения задачи преподаватель разъясняет студентам, в чем проявляет себя отличие реальных задач коммивояжера от рассмотренного примера.
У доски студентами решается задача коммивояжера при N = 10.
На доске записывается исходная матрица, элементами которой являются «расстояния» между городами хi и хj, т. е. Сij.
Число возможных вариантов маршрута определяется как факториал m = (N – 1)! и для N = 10 m! = 362880.
В дополнительный столбец табл. 3.2 выносятся при построчном просмотре те элементы строки, которые содержат «расстояния» с наименьшим значением. Сумма элементов дополнительного столбца соответствует минимальной «длине маршрута» и используется для сравнительной оценки сформированных студентами вариантов маршрутов.
Таблица 3.2
Город |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Дополн. столбец |
1 |
|
3 |
4 |
4 |
3 |
3 |
6 |
6 |
5 |
2 |
2 |
2 |
5 |
|
4 |
4 |
5 |
2 |
3 |
3 |
2 |
4 |
2 |
3 |
6 |
7 |
|
6 |
7 |
7 |
6 |
7 |
7 |
6 |
6 |
4 |
2 |
3 |
4 |
|
2 |
3 |
4 |
2 |
3 |
4 |
2 |
5 |
7 |
6 |
5 |
4 |
|
7 |
6 |
5 |
4 |
7 |
4 |
6 |
2 |
4 |
3 |
5 |
6 |
|
4 |
2 |
3 |
4 |
2 |
7 |
4 |
3 |
2 |
2 |
3 |
4 |
|
3 |
4 |
4 |
2 |
8 |
5 |
3 |
3 |
5 |
4 |
3 |
2 |
|
3 |
4 |
2 |
9 |
6 |
4 |
2 |
3 |
5 |
7 |
3 |
5 |
|
3 |
2 |
10 |
3 |
4 |
5 |
3 |
4 |
5 |
2 |
3 |
4 |
|
2 |
Один из студентов строит приведенную матрицу по строкам (табл. 3.3).
Таблица 3.3
Город |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
1 |
|
1 |
2 |
2 |
1 |
1 |
4 |
4 |
3 |
0 |
2 |
3 |
|
2 |
2 |
3 |
0 |
1 |
1 |
0 |
2 |
3 |
0 |
1 |
|
0 |
1 |
1 |
0 |
1 |
1 |
0 |
4 |
0 |
1 |
2 |
|
0 |
1 |
2 |
0 |
1 |
2 |
5 |
3 |
2 |
1 |
0 |
|
3 |
2 |
1 |
0 |
3 |
6 |
0 |
2 |
1 |
3 |
4 |
|
2 |
0 |
1 |
2 |
7 |
2 |
1 |
0 |
0 |
1 |
2 |
|
1 |
2 |
3 |
8 |
3 |
1 |
1 |
3 |
2 |
1 |
0 |
|
1 |
2 |
9 |
4 |
2 |
0 |
1 |
3 |
5 |
1 |
3 |
|
1 |
10 |
1 |
2 |
3 |
1 |
2 |
3 |
0 |
1 |
2 |
|
Для того чтобы не производить полный перебор вариантов маршрута (из 362880), осуществляется классификация элементов матрицы на «лучшие и «нехудшие».
«Лучшие» – это элементы приведенной матрицы со значением, равным нулю.
«Нехудшие» – это элементы приведенной матрицы со значением, близким к нулю.
Студенты анализируют приведенную матрицу и формируют два подмножества: «лучших» и «нехудших», которые записываются раздельно одним из студентов на доске.
Затем студенты по очереди у доски формируют варианты маршрутов, выбирая элементы из этих двух множеств. Целесообразно маршрут коммивояжера составлять только из «лучших» элементов. «Нехудшие» элементы подставляются тогда, когда коммивояжер уже посетил данный город, которому соответствует «лучший» элемент.
Таблица 3.4
Подмножество |
|
«Лучшие» |
«Нехудшие» |
C1,10 C2,6, C2,9 C3,1, C3,4, C3,7, C3,8 C4,1, C4,5, C4,8 C5,4, C5,9 C6,1,C6,8 C7,3, C7,4 C8,7 C9,3 C10,7 |
C1,2, C1,5, C1,6 C2,7, C2,8 C3,2, C3,5, C3,6, C3,9, C3,10 C4,2 C4,6 C4,9 C5,3, C5,8 C6,3, C6,9 C7,2, C7,5, C7,8 C8,2, C8,3, C8,6, C8,9 C9,4, C9,7, C9,10 C10,1, C10,4, C10,8 |
N1 = 19 |
N2 = 30 |
Варианты маршрутов:
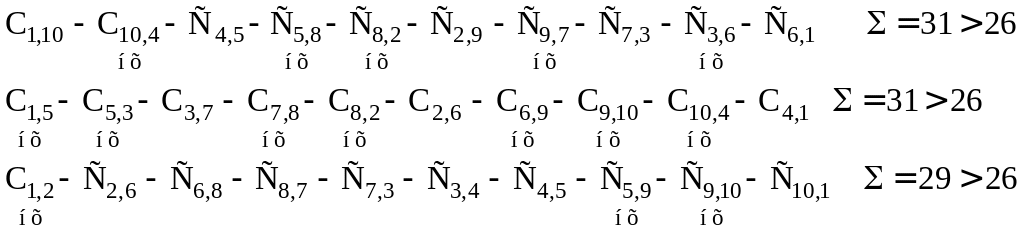
В конце практического занятия под руководством преподавателя студенты выбирают в качестве оптимального маршрут коммивояжера из числа сформированных с наименьшим отличием от минимальной «длины маршрута» пути. Если таких вариантов два и более, требуется дополнительное условие для выбора компромиссного варианта маршрута.