Выполнил: Мотигуллин Р.Р. гр.4109.

1.Что такое предикат-

1) Совокупность всех подмножеств множества А.

2) Это некоторые условия выраженное в форме логического утверждения , которое истинно, тогда и только тогда, когда х удовлетворяет этому условию. +

3) Это некоторое условие, в которой будучи запущенной, порождает некоторые объекты, являющиеся элементами определяемого множества.

4) Совокупность определённых и различных между собой объектов, мыслимых как единое целое.

2.Множество обозначается скобками , внутри которых…

1) Перечисляются элементы.

2) Описываются свойство элементов.

3) Перечисляются элементы и описываются их свойства. +

4) Элементы записываются по возрастанию или по убыванию.

3.Множества А и B состоящие из одних и тех же элементов, называют …

1) Равными. +

2) Буленами.

3) Подмножествами.

4) Несобственными.

4. Перечислить способы задания множеств.

1) Перечисления, порождающая процедура.

2) Перечисления, предикат.

3) Перечисления, предикат, порождающая процедура. +

4) Предикат, порождающая процедура.

5.Сколько аксиом в аксиоматики Цермело-Френкеля.

1) 3.

2) 5.

3) 8.

4) 12.+

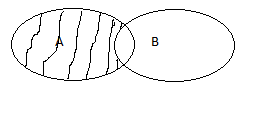
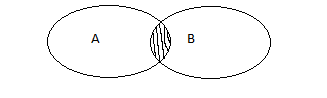
6. Какой из рисунков, является операцией разности.

1)

2 )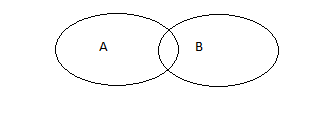

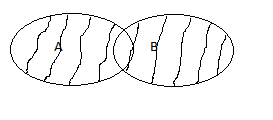
3)+

4)

7.Какое из данных операцией является определением для пересечения множеств.

1) Называется множество, элементы которого являются элементами обоих множеств А и В.+

2) Называется множество, каждый элемент которого является элементом множества А или множеством В.

3) Называется множество, каждый элемент который принадлежит множеству А и не принадлежит множеству В.

4) Называется множество, элементы которого не являются элементами обоих множеств А и В.

8.Какой из данных законов является коммутативным.

1) АВ=ВА, АВ=ВА. +

2) А(ВС)=(АВ)С, А(ВС)=(АВ)С.

3) А(АВ)=А, А(АВ)=А.

4) АА=А, АА=А.

9.Какое из данных свойств является дополнением.

1) АU=U, А=.

2) АА=U, AA=. +

3) (A)=A.

4)A=A.

10.Выбрать символ объединения.

1) .

2) .

3) .

4) . +

11.Семейство подмножеств {B1,B2,…, Bn} ,образует разбиение множества А тогда и только тогда, когда

1) Bi≠, 1≤i≤n

2) Bi≠, 1≤i≤n;BiBj= если i≠j;B1B2…Bn=A. +

3) BiBj= если i≠j;B1B2…Bn=A.

4) Bi≠, 1≤i≤n;BiBj= если i≠j.

12.Упорядоченной парой называется объект (a,b) такой, что (a,b)=(c,d) тогда и только тогда, когда

1) a=c и b=d.+

2) a=b и c=d.

3) a=d и c=b.

4) a=c=b=d.

13. Декартовым (прямым) произведением двух множеств А и В называется множество упорядоченных пар (a,b), таких, что

1) aA bB.

2) aA bB.

3) aA bB.+

4) aA bB.

14. Декартово (прямое) произведение обозначается через

1) А\В.

2) А+В.

3) А-В.

4) А*В. +

15. Упорядоченной n-кой элементов а1, а2,…,аn , а1А1,а2А2,аnAn, называется объект (а1,а2,…,аn), такой что (а1,а2,…,аn)=(b1,b2,…,bn), b1A1, b2A2,… bnAn, тогда и только тогда, когда

1) а1=b1,a2=b2,…,an=bn.+

2) a1=b2,a2=b1,…,a(n-1)=bn.

3) a1=a2,b1=b2,…,a(n-1)=an b(n-1)=bn.

4) a1=b1=…=an=bn.

16.Бинарным отношением на (двух) множествах А и В называется

1) подмножество R декартового произведения АВ.+

2) множество R декартового произведения АВ.

3) элемент R декартового произведения АВ.

4) объект R декартового произведения АВ.

17.Областью определения бинарного отношения R называется множество

1) D_R={xA:существует такое yB, что xRy}.+

2) D_R={xA:существует такое yB, что xRy}.

3) D_R={xA:существует такое yB, что xRy}.

4) D_R={xA:существует такое yB, что xRy}.

18.Областью значений бинарного отношения R называется множество

1) Im_R={yB: существует такое xA, что xRy}.

2) Im_R={yB: существует такое xA, что xRy}.

3) Im_R={yB: существует такое xA, что xRy}.+

4) Im_R={yB: существует такое xA, что xRy}.

19.Пустое отношение определяется пустым

1) объектом множества АВ.

2) элементом множества АВ.

3) множеством АВ.

4) подмножеством множества АВ.+

20.Сколько существует способов задания отношения R:

1) 3.

2) 7. +

3) 5.

4) 4.

21.Пусть R – отношение на множествах А и В, S-отношение на множествах B и C. Тогда композицией R и S называется отношение обозначаемое как

1) RS.+

2) RS.

3) RS.

4) RS.

22.Бинарное отношение R на множестве А называется рефлексивным, если

1) для аА а,аR.

2) для аА а,аR.

3) для аА а,аR.

4) для аА а,аR.+

23. Бинарное отношение R на множестве А называется симметричным, если

1) из х,уR следует, что х.у R.

2) из х,уR следует, что х,у R.

3) из х,уR следует, что у,х R.

4) из х,уR следует, что у,х R.+

24. Бинарное отношение R на множестве А называется транзитивным, если

1) из х,уR и у,zR следует, что х,zR.

2) из х,уR и у,zR следует, что х,zR.

3) из х,уR и у,zR следует, что х,zR.+

4) из х,уR и у,zR следует, что х,zR.

25.Как обозначается операция пересечение отношения:

1)R_{1 }R₂.

2) R₁ R₂. +

3) R₁ R₂.

4) R₁ R₂.

26.Бинарное отношение f на множествах А и В называется функцией, если образ каждого элемента (при этом отношении) единственен, т.е.

1) из х,уf и  x,zf следует, что y=z.+

2) из х,уf и  x,zf следует, что yz.

3) из х,уf и  x,zf следует, что y=z.

4) из х,уf и  z,xf следует, что y=z.

27.Функцию f(с областью определения D_f и с областью значения Im_f, Im_f В) иногда называют:

1) отображением множества А. +

2) определенное множество А.

3) частично определенное множество А.

4) неопределенным множеством А.

28.Функция f называется инъективной, если для:

1) х₁,х₂ из f(x₁)f(x₂) следует, что х₁=х₂.

2) х₁,х₂ из f(x₁)=f(x₂) следует, что х₁=х₂.

3) х₁,х₂ из f(x₁)=f(x₂) следует, что х₁=х₂.+

4) х₁,х₂ из f(x₁)=f(x₂) следует, что х₁х₂.

29.Функция f(f:AB) называется сюръективной, если для любого

1) уВ существует хА такой, что у=f(x).

2) уВ существует хА такой, что у=f(x).

3) уВ существует хА такой, что уf(x).

4) уВ существует хА такой, что у=f(x). +

30. Функция f(f:AB) называется биективной, если f:

1) не инъективна и не сюръективна.

2) инъективна и сюръективна. +

3) не инъективна и сюръективна.

4) инъективна и не сюръективна.

31.Бинарное отношение R на множестве А называется отношением эквивалентности, если R:

1) рефлексивно, симметрично и транзитивно.+

2) рефлексивно.

3) симметрично и транзитивно.

4) рефлексивно и транзитивно.

32.Классом эквивалентности (классом смежности), порожденным элементом а при данном отношении эквивалентности R, называется:

1) элементы тех хА, которые находятся в отношении R с а.

2) множество тех хА, которые находятся в отношении R с а.

3) подмножество тех хА, которые находятся в отношении R с а.+

4) объекты тех хА, которые находятся в отношении R с а.

33.Различные отношения эквивалентности на множестве А порождают

1) одинаковое разбиение А.

2) одинаковые и различные разбиения А.

3) различные разбиения А.+

4) не происходит разбиение А.

34.Каждое разбиение множества А

1) порождает отношение эквивалентности на множестве А. +

2) предикует отношение эквивалентности на множестве А.

3) буленует отношение эквивалентности на множестве А.

4) разрушает отношение эквивалентности на множестве А.

35.Для любых целых a,b,a*,b*,k m

1) a+a*b+b* (mod m). +

2) a+a*b+b* (mod k).

3) a+a*b+b* (mod m,k).

4) a+a*b+b* (mod k,m).

36.Бинарное отношение R на множестве А называется отношением частичного порядка, если R

1) рефлексивно, антисимметрично.

2) рефлексивно, антисимметрично и транзитивно.+

3) антисимметрично и транзитивно.

4) рефлексивно, транзитивно.

37. Бинарное отношение R на множестве А называется отношением строгого порядка, если R

1) антисимметрично и транзитивно.

2) рефлексивно, транзитивно.

3) рефлексивно, антисимметрично и транзитивно.+

4) рефлексивно, антисимметрично.

38. Частично упорядоченного множество, в котором любые два элемента сравнимы, называется

1) частично упорядоченным множеством.

2) упорядоченным множеством.

3) строго упорядоченным множеством.

4) линейно упорядоченным множеством.+

39. Отношение х<y на (-,) является отношением

1) частичного порядка.

2) строгого порядка.+

3) частичного и строгого порядка.

4) не существует такого порядка.

40. Частично упорядоченное множество, в котором любые два элемента сравнимы,

называется

1) линейно упорядоченным множеством.+

2) частично упорядоченным множеством.

3) строго упорядоченным множеством.

4) линейно и частично упорядоченным множеством.

Глава 2.

41.Если множество А является декартовым произведением n множеств, то аргументом функции f: AB является

1) упорядоченная n-ка.+

2) строго упорядоченная n-ка.

3) линейно упорядоченная n-ка.

4) частично упорядоченная n-ка.

42.Функцию : СⁿС называют

1) n-показательной.

2) n-степенной.

3) n-арной.+

4) n-аргументной.

43.Предикатом от n аргументов называется функция

1) с областью определения СС…С, n3, и областью значений, равной множеству {И,Л}.

2) с областью определения СС…С, n1, и областью значений, равной множеству {И,Л}.+

3) с областью определения СС…С, n1, и областью значений, равной множеству {М,Л}.

4) с областью определения СС…С, n1, и областью значений, равной множеству {Л,М}.

44.n-местный предикат Р отображает Сⁿ в (на) множество

1){И,Л}.+

2) {Л,И}.

3) {М,Л}.

4) {Л,М}.

45.Пусть С=(-,), А=СС и Р(х,у) обозначает х>у. Тогда

1) Р(3,1)=И, Р=(3,5)=Л.+

2) Р(3,1)=Л, Р=(3,5)=И.

3) Р(3,1)=И, Р=(3,5)=И.

4) Р(3,1)=Л, Р=(3,5)=Л.

46.Алгебраической системой называют

1) непустое множество А с введенными на этом множестве предикатами.

2) непустое множество А с введенными на этом множестве операциями.

3) пустое множество А с введенными на этом множестве операциями и предикатами.

4) непустое множество А с введенными на этом множестве операциями и предикатами.+

47.Алгебраическая система А;_F,_P называется алгеброй, если

1) _Р и _F=.

2) _Р= и _F=.

3) _Р и _F.

4) _Р= и _F.+

48. Алгебраическая система А;_F,_P называется моделью, если

1) _Р и _F=.+

2) _Р= и _F=.

3) _Р и _F.

4) _Р= и _F.

49.Алгебра-непустое множество А, на котором задана совокупность операций, переводящих элементы

1) из А в А.+

2) из А в В.

3) из В в А.

4) из В в В.

50.Пусть имеем алгебру с n операциями F₁,F₂,…,F_n и пусть m_i число аргументов операции F_i(1in).Тогда вектор =(m₁,m₂,…,m_n) называют

1) типом алгебры.+

2) элементом алгебры.

3) носителем алгебры.

4) множество алгебры.

51.Подмножество В множества А называется замкнутым относительно операции F_i переводит элементы

1) из В в А.

2) из В в В.+

3) из А в А.

4) из А в В.

52.Пусть имеем алгебру А;_F, здесь

1) _F-множество n операции на непустом множестве А.+

2) _F-подмножество n операции на непустом множестве А.

3) _F- множество n операции на пустом множестве А.

4) _F- подмножество n операции на пустом множестве А.

53.Если подмножество В (ВА) замкнуто относительно всех операций алгебры, то В=В;_F называют

1) подалгеброй алгебры В, _F.

2) подмножество алгебры В, _F.

3) подмножество алгебры А, _F.

4) подалгеброй алгебры А, _F.+

54.Пусть А=[0,) и введем операции сложения (+) и умножения (). Множество натуральных чисел N содержится в А замкнуто относительно операций + и . Поэтому

1) N порождает подмножество в алгебре [0,);+,.

2) N порождает подалгебру в алгебре [0,);+,.+

3) N порождает подалгебру в алгебре [0,);+.

4) N порождает подмножество в алгебре [0,);+.

55.Пересечение любой совокупности подалгебр данной алгебры

1) либо непусто, либо является подалгеброй данной алгебры.

2) либо пусто, либо является подалгеброй данной алгебры.+

3) либо непусто, либо является подмножеством данной алгебры.

4) либо пусто, либо является подмножество данной алгебры.

56.Всякое отображение  основного множества А в(на) основное множество В называем

1) отображением алгебры А в(на) алебру В.+

2) изоморфизмом алгебры А в(на) алебру В.

3) гоморфизмом алгебры А в(на) алебру В.

4) отображением алгебры А в(на) алебру А.

57.Изоморфизмом алгебры А=А; F₁, F₂,…, F_n в(на) однотипную алгебру В=В; G₁,G₂,…,G_n называется взаимно однозначное (биективное) отображение 

1) множество А в(на) В, сохраняющее главные операции алгебры.+

2) множество А в(на) А, сохраняющее главные операции алгебры.

3) множество В в(на) В, сохраняющее главные операции алгебры.

4) множество А , сохраняющее главные операции алгебры.

58.Гоморфизмом алгебры А=А; F₁, F₂,…, F_n в(на) однотипную алгебру В=В; G₁,G₂,…,G_n называется отображенеие 

1) множества В в(на) множество В, сохраняющее главные операции алгебры.

2) множества А в(на) множество А, сохраняющее главные операции алгебры.

3) множества А в(на) множество В, несохраняющее главные операции алгебры.

4) множества А в(на) множество В, сохраняющее главные операции алгебры.+

59.Изоморфизм алгебры на себя называется

1) автоизоморфизм.

2) автоморфизм.+

3) автогоморфизм.

4) морфизм.

60.Отображение : АВ сохраняет операцию, но это отображение не является изоморфным, так как различные матрицы могут иметь

1) одинаковый определитель.+

2) различный определитель.

3) одинаковый и различный определитель.

4) пустой определитель.

61.Самой простой алгеброй является

1) пустое множество G с двумя двуместной (бинарной) операцией.

2) непустое множество G с двумя двуместной (бинарной) операцией.

3) пустое множество G с одной двуместной (бинарной) операцией.

4) непустое множество G с одной двуместной (бинарной) операцией.+

62.Множество с одной двуместной операцией называют

1) пустая группа.

2) полугруппа.

3) группа.

4) группоид.+

63.Множество G, на котором введена одна ассоциативная двуместная (бинарная) операция

1) пустая группа.

2) полугруппа.+

3) группа.

4) группоид.

64.Моноид-это

1) пустая группа.

2) полугруппа с единицей.+

3) группа с единицей.

4) группоид.

65.Всякий моноид над множеством М изоморфен некоторому моноиду преобразований над

1) М.+

2) А

3) В

4) G

66.Группа-это моноид, в котором для любого элемента существует

1) группа элементов.

2) прямой элемент.

3) обратный элемент.+

4) полугруппа элементов.

67.Множество G с одной бинарной операций “” называем группой, если:

1) существует единица в G,для любого элемента аG существует обратный элемент.

2) операция ассоциативна, для любого элемента аG существует обратный элемент.

3) операция ассоциативна, существует единица в G,для любого элемента аG существует обратный элемент.+

4) операция ассоциативна, существует единица в G.

68.Если операция в группе называется умножением, то группа называется

1) мультипликативной.+

2) аддитивной.

3) пликативной.

4) дитивной.

69.Если групповая операция называется сложением, то группа называется

1) мультипликативной.

2) аддитивной.+

3) пликативной.

4) дитивной.

70.Группа с одной образующей называется

1) коммутативной.

2) образующей.

3) циклической.+

4) абелевой.

71.Кольцом называется непустое множество R, на котором введены

1) одна бинарная операции .

2) одна бинарная операции + .

3) две бинарные операции + и .+

4) две бинарные операции + и -.

72.Кольцо называется коммутативным, если для

1) a,bR:ab=ba.+

2) a,bR:ab=ba.

3) a,bR:ab=ba.

4) a,bR:ab=b.

73.Коммутативное кольцо без делителей нуля, отличных от тривиального делителя нуля, называют

1) множественным кольцом.

2) элементным кольцом.

3) образующим кольцом.

4) целостным кольцом.+

74.Если в кольце R имеем, что ab=0, то элемент 0 считаем

1) тривиальным делителем.+

2) левым делителем.

3) правым делителем.

4) бинарным делителем.

75. Если в кольце R имеем, что ab=0, то a называется

1) тривиальным.

2) левым.+

3) правым.

4) бинарным.

76. Если в кольце R существует единица относительно умножения, то эту мультипликативную единицу обозначают через

1) 1 и 0.

2) 0.

3) 1.+

4) .

77.Элементы 0 и 1 являются

1) различными элементами нулевого кольца R.

2) одинаковыми элементами нулевого кольца R.

3) одинаковыми элементами ненулевого кольца R.

4) различными элементами ненулевого кольца R.+

78.Аддитивная единица, то есть

1) 1, не имеет аддитивного обратного.

2) 0, не имеет аддитивного обратного.

3) 1, не имеет мультипликативного обратного.

4) 0, не имеет мультипликативного обратного.+

79.Характеристикой кольца R называют наименьшее натуральное число k такое, что

1) a+a+…+a=0 для всех aR.+

2) a+a+…+a=0 для всех aR.

3) a-a-…-a=0 для всех aR.

4) a-a-…-a=0 для всех aR.

80.Характеристика кольца записывается

1) k=charR.+

2) k=setR.

3) k=resetR.

4) k=gradR.

81.Полем называется коммутативное кольцо

1) у которого нулевые элементы образуют коммутативную группу относительно сложения.

2) у которого ненулевые элементы образуют коммутативную группу относительно сложения.

3) у которого нулевые элементы образуют коммутативную группу относительно умножения.

4) у которого ненулевые элементы образуют коммутативную группу относительно умножения.+

82.Поле-это множество P с двумя бинарными операциями

1) + и .+

2) + и -.

3)  и /.

4) / и -.

83.Если a0, то в поле единственным образом разрешимо уравнение

1) a+x=b.

2) a-x=b.

3) ax=b.+

4) a/x=b.

84.Для любого ненулевого элемента (а0) существует

1) обратный элемент по умножению.+

2) прямой элемент по умножению.

3) обратный элемент по сложению.

4) прямой элемент по сложению.

85.R;+,x-это

1) поле рациональных чисел.

2) поле вещественных чисел.+

3) поле комплексных чисел.

4) поле иррациональных чисел.

86.Решетки иногда называют

1) списками.

2) графами.

3) структурами.+

4) таблицами.

87.Решетка-это множество М с двумя бинарными операциями

1) + и .

2)  и .+

3)  и .

4) + и .

88.Если в решетке  0М, что для а: 0а=0, то 0 называется

1) нижней гранью.+

2) средней гранью.

3) верхней гранью.

4) гранью.

89.В ограниченной решетке элемент а’ называется дополнением элемента а,если

1) aa’=1 и aa’=1.

2) aa’=0 и aa’=1.+

3) aa’=0 и aa’=0.

4) aa’=1и aa’=0.

90.Пусть ab  ab=a.Тогда отношение  является отношением

1) частичного порядка.+

2) полного порядка.

3) выборочного порядка.

4) нулевого порядка.

91.Дистрибутивная ограниченная решетка, в которой для каждого элемента существует дополнение, называется

1) алгеброй.

2) булевой.

3) булевой алгеброй.+

4) дистрибутивной алгеброй.

92.М, 2^м,,,-, здесь

1) 12^м,0, АВ  АВ.

2) 12^м,0=, АВ  АВ.

3) 1=2^м,0, АВ  АВ.

4) 1=2^м,0=, АВ  АВ.+

93.Так как дополнение существует, то

1) аa’=0, aa’=0.

2) аa’=1, aa’=1.

3) аa’=0, aa’=1.

4) аa’=1, aa’=0.+

94.По теореме о свойствах дополнения

1) а”=a.+

2) а”a.

3) а’=a.

4) а’a.

95.По следствию из теоремы ограниченности, следует что

1) а1=а, а0=а.

2) а0=а, а0=а.

3) а0=а, а1=а.+

4) а1=а, а1=а.

96.Матроидом М=Е;Х называется конечное множество Е, Е=n, и семейство его подмножеств Х, для

1) Х2^Е.+

2) Е2^Х.

3) Х2^Е.

4) Е2^Х.

97. Матроидом М=Е;Х называется конечное множество Е, что выполняется следующие аксиомы

1) Х; АХ и ВА, то ВХ.

2) Х; если А,ВХ и В=А+1,то е, еВ\А, такой, что А{e}Х.

3) АХ и ВА, то ВХ; А,ВХ; если А,ВХ и В=А+1,то е, еВ\А, такой, что А{e}Х.

4) Х; АХ и ВА, то ВХ; А,ВХ; если А,ВХ и В=А+1,то е, еВ\А, такой, что А{e}Х.+

98.График одноаргументной функции у=f(x) (хА, уА) является

1) объектом декартового произведения АА..

2) элементом декартового произведения АА..

3) множеством декартового произведения АА..

4) подмножеством декартового произведения АА,+

99.Матроидом называется конечное множество Е и семейство С={С₁,С₂,С₃,…,С_m}

1) непустых множеств множества Е, называемых циклами.

2) пустых подмножеств множества Е, называемых циклами.

3) непустых подмножеств множества Е, называемых циклами,+

4) пустых подмножеств множества Е, называемых циклами.

100.Какие аксиомы справедливы для цикла

1) ни одно собственное подмножество цикла есть цикл; если х(С₁С₂), то (С₁С₂)\{х} содержит цикл.

2) ни одно собственное подмножество цикла не есть цикл; если х(С₁С₂), то (С₁С₂)\{х} содержит цикл,+

3) одно собственное подмножество цикла не есть цикл; если х(С₁С₂), то (С₁С₂)\{х} содержит цикл.

4) если х(С₁С₂), то (С₁С₂)\{х} содержит цикл.