
- •Введение
- •1. Геолого-физические условия и состояние разработки месторождения
- •1.1. Общие сведения о месторождении
- •1.2. Геологическая характеристика района
- •1.2.1 Стратиграфия
- •1.2.2 Тектоника
- •1.2.3 Нефтегазоносность
- •1.2.4 Геолого-промышленная характеристика месторождения
- •Выводы к разделу 1
- •2. Технологический раздел
- •1.5 Характеристика фонда скважин
- •2.4. Анализ примененных на данном месторождении технических решений для интенсификации добычи нефти
- •2.5. Анализ выработки запасов нефти
- •2.6. Анализ эффективности реализуемой системы разработки
- •2.7. Обоснование и выбор проектируемого технического решения для интенсификации добычи нефти
- •2.8. Проектирование технического решения для реализации на данном месторождении
- •2.9. Определение технологической эффективности при реализации технического решения
- •2.9.1.Исходные данные для определения технологической эффективности
- •2.9.2 Выбор метода определения технологической эффективности
- •2.9.3 Расчет технологической эффективности при реализации проектируемого технического решения
- •2.9.3 Методика расчета по Мукминову и.Р. Горизонтальной скважины
- •2.9.4 Расчет дебита горизонтальной скважины.
- •2.9.5 Расчет дебита вертикальной скважины.
- •2.9.6. Сравнение технологических показателей проектируемого технического решения
- •2.9.7. Проектирование солянокислотной обработки
- •Выводы к разделу 2
- •Заключение
- •Список использованных источников и литературы
2.9. Определение технологической эффективности при реализации технического решения
2.9.1.Исходные данные для определения технологической эффективности
Исходными данными для определения технологической эффективности применения боковых горизонтальных стволов и горизонтальных скважин понадобятся следующие исходные данные по скважинам (приведены в таблице 15).
Таблица 15. Исходные данные для определения технологической эффективности
Показатель |
Значение |
Режим разработки |
Естественный |
Сетка размещения скважин |
неравномерная |
Расстояние между скважинами, м |
200 х 375 |
Плотность сетки скважин, га/скв |
неравномерная |
Пластовое давление,
|
16,1 МПа |
Коэффициент проницаемости,
|
0,216 |
Толщина пропластка, h |
11,5 м |
Вязкость нефти в пластовых условиях, |
98,4
|
Вязкость пластовой воды, |
1,5 |
Давление на забое добывающей скважины,
|
10 МПа |
Радиус контура питания, |
300 м |
Радиус скважины,
|
0,146 м |
Длина горизонтального участка БГС, L |
150 м |
Водонасыщенность, s |
16 % |
Коэфф. охвата процессом вытеснения, д.ед |
0,665 |
Коэффициент эксплуатации |
0,94 |
|
|
2.9.2 Выбор метода определения технологической эффективности
При решении практических задач проектирования и анализа разработки нефтяных месторождений одной из основных формул для оценки дебитов скважин является известная формула Дюпюи. Поэтому естественным образом возникает вопрос получения аналога формулы Дюпюи и для притока жидкости в горизонтальную скважину.
Рассмотрим задачу о квазистационарном течении жидкости в пористой среде. Одиночная горизонтальная скважина длиной L дренирует область, ограниченную контуром питания с радиусом Rк. Толщина пласта - h, абсолютная проницаемость - K, динамическая вязкость жидкости - m, давление на контуре питания - pк, давление на забое скважины - pс, приведенный радиус скважины - rс. Требуется определить дебит скважины.
Наиболее простое решение было предложено Ю.Т.Борисовым и В.П.Табаковым.
Дебит горизонтальной скважины выражается формулой
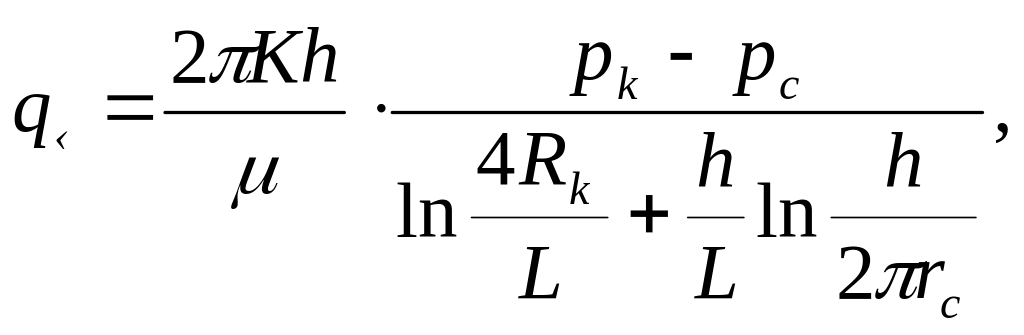 (1)
(1)
Первое слагаемое в знаменателе отражает внешнее фильтрационное сопротивление, вторе слагаемое - внутреннее сопротивление скважины.
Внешне фильтрационное сопротивление по форме совпадает с сопротивлением вертикальной скважины, отличаясь лишь тем, что вместо радиуса скважины rс используется радиус rэкв = L / 4. Внутреннее сопротивление горизонтальной скважины принимается по методу эквивалентных фильтрационных сопротивлений Ю.П. Борисова равным внутреннему сопротивлению батареи вертикальных скважин шириной L, расстояние между скважинами 2×d = h.
Формула (1) имеет тот недостаток, что вне зависимости от длины горизонтальной скважины контур питания предполагается радиальным. Точность данной формулы должна убывать с ростом отношения L/Rк.
Для горизонтальной скважины контур нефтеносности должен иметь эллипсообразный, а не круговой характер. С учетом этого Giger F. представил формулу притока в горизонтальную скважину в виде
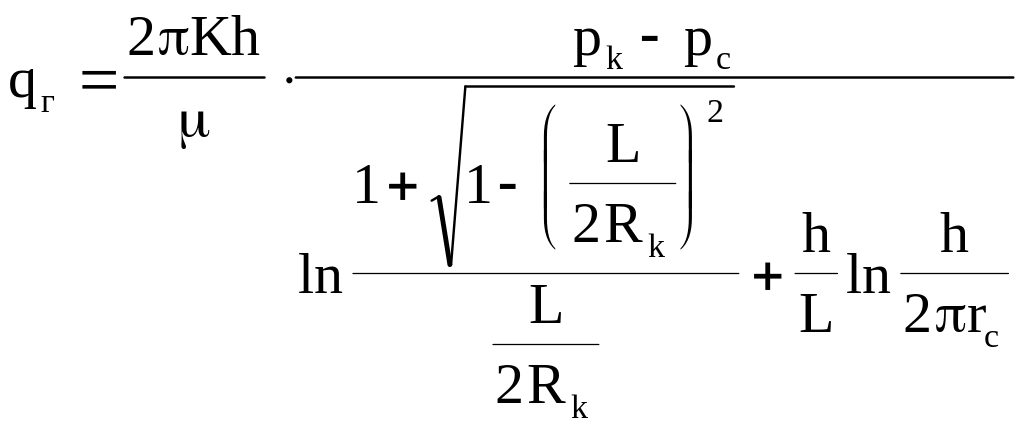 , (2)
, (2)
где Rк - большая полуось эллипса, являющегося контуром питания.
Joshi S. в развитие формулы (2) получил выражение
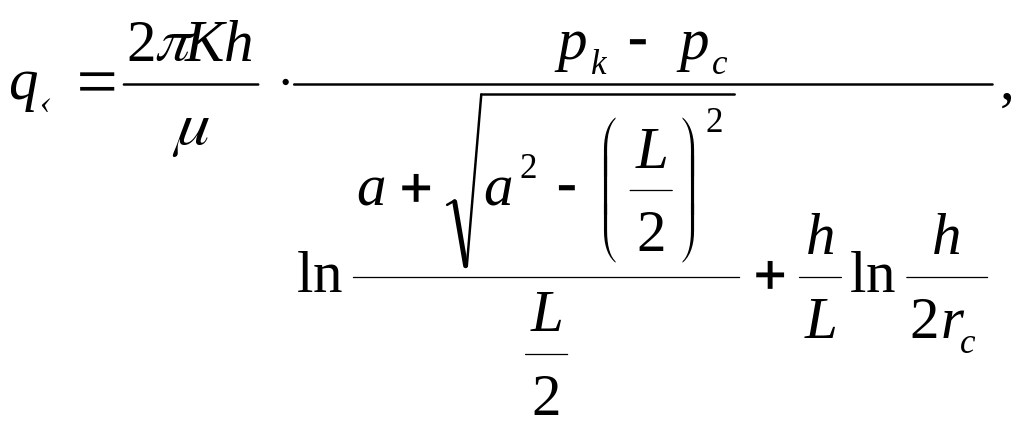 (3)
(3)
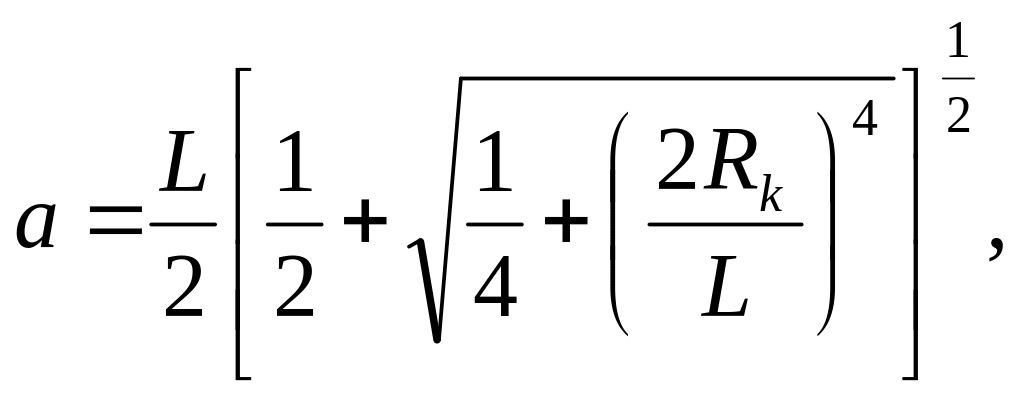 (4)
(4)
где
![]() есть большая полуось эллипса, равновеликого
по площади кругу с радиусом дренирования
Rк. Есть некоторое
различие в определении внутреннего
сопротивления горизонтальной скважины
в формулах (3) и (1) - (2). В формуле (3)
внутреннее сопротивление несколько
выше, чем в формулах (1) и (2). По методу
эквивалентных фильтрационных сопротивлений
более правильно отражают внутреннее
сопротивление формулы (1) и (2).
есть большая полуось эллипса, равновеликого
по площади кругу с радиусом дренирования
Rк. Есть некоторое
различие в определении внутреннего
сопротивления горизонтальной скважины
в формулах (3) и (1) - (2). В формуле (3)
внутреннее сопротивление несколько
выше, чем в формулах (1) и (2). По методу
эквивалентных фильтрационных сопротивлений
более правильно отражают внутреннее
сопротивление формулы (1) и (2).
Еще одна формула предложена в работе Renard G., Dupuy J.
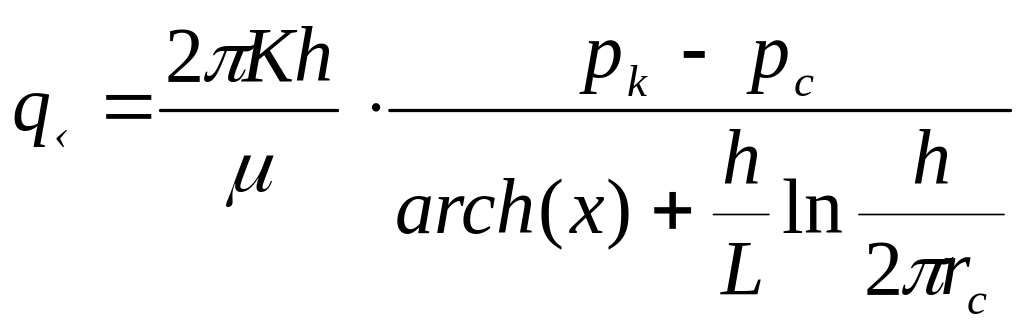 , (5)
, (5)
где x = 2a / L и a вычисляются по формуле (4).
Формула (5) по внешнему фильтрационному сопротивлению совпадает с формулой (3), а по внутреннему сопротивлению - с формулами (1) и (2).
Формулы (1) - (5) соответствуют случаю изотропного по проницаемости пласта.
С учетом анизотропии по проницаемости Joshi предложена формула
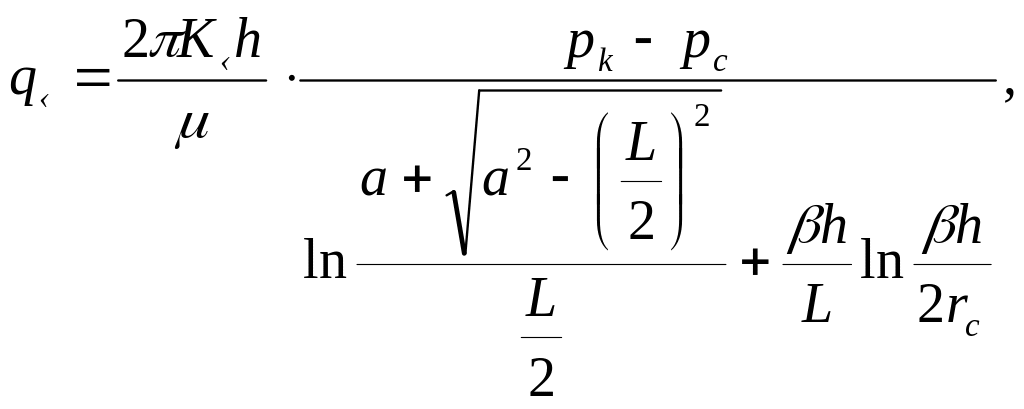 (6)
(6)
где
![]() - коэффициент анизотропии; Kг
- проницаемость пласта в горизонтальном
направлении; Kв -
проницаемость по вертикали.
- коэффициент анизотропии; Kг
- проницаемость пласта в горизонтальном
направлении; Kв -
проницаемость по вертикали.
Формула Renard, Dupuy для анизотропного пласта
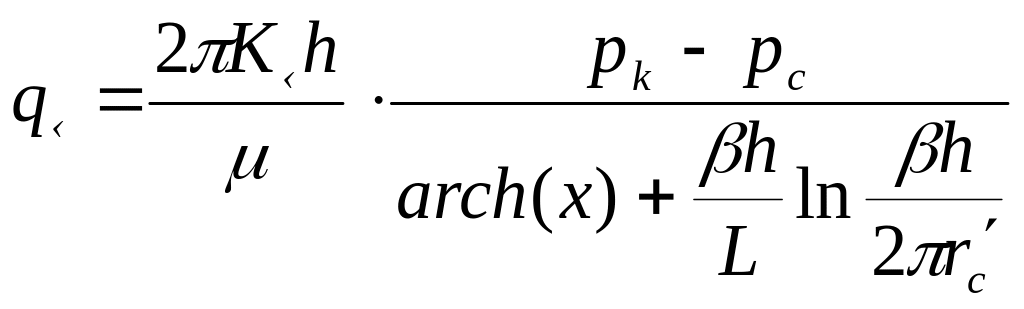 ,
(7)
,
(7)
где
![]()
