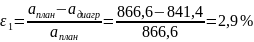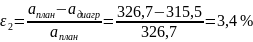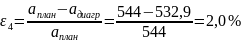3. Расчет ускорений

Расчет ускорений проводится для трёх положений рабочего хода механизма, в которых сила полезного сопротивления не равна нулю. Ускорения определяются подобно скоростям, расчет которых был проделан выше (п. 2.1.2). В данном курсовом проекте рассчитываются линейные и угловые ускорения в положениях механизма №1, №2 №4.

Первоначально определим ускорение точки А кривошипа. Оно является постоянным и равно произведению квадрата угловой скорости кривошипа на его длину:

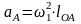. (2.5)

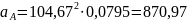м/с² .

Нахождение ускорений будем производить методом планов, для этого запишем векторное уравнение ускорения точки B:

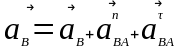(2.6)

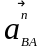где и 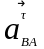- нормальная и тангенциальная составляющие ускорения звена АС соответственно.

Решим уравнение (2.6) графически. Для этого примем масштабный коэффициент плана ускорени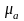й , равный:

,

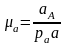Где 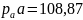мм.

.

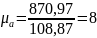
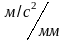Строим план ускорений согласно направлению векторов:

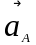- направлено из точки А в точку О₁;

- направлено из точки B в точку А;

- направлено перпендикулярно звену АB;

- направление 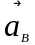задается вертикальной направляющей t – t.

Определим нормальную составляющую ускорения звена АВ:

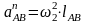, (2.7)

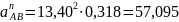м/с².

Для построения плана ускорений:

• выбираем полюс р_а (рис. 2.1.5);

• строим вектор ускорения ;

• из конца вектора строим луч параллельный звену АB, и на этом луче откладываем отрезок

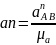
• через точку n проводим прямую перпендикулярную АB, отмечаем точку пересечения ее с вертикальной направляющей t-t – точка b;

• отрезок р_аb – ускорение точки B на плане ускорений.

Ускорения центров масс определяем по принципу подобия:

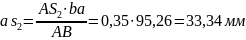
План ускорений для положения №2 представлен на рис. 2.1.5

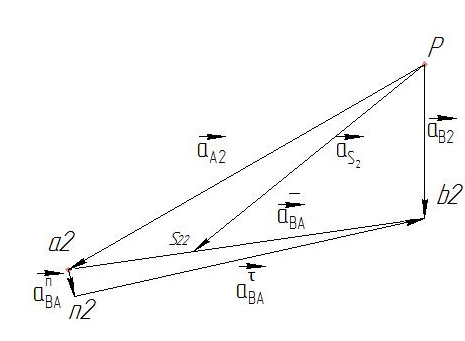
Рис. 2.1.5 План ускорений для положения №2

Численные значения ускорений вычислим по формулам:

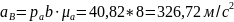
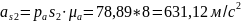
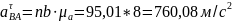
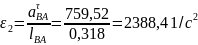
Полученные значения всех ускорений для положений механизма №1, №2 и №4 приведены в таблице 3.

Таблица 3

	aa	aB	aBA	as2	ε2
№1	870,97	866,56	450,16	844,32	1315,97
№2		326,72	762,08	631,12	2390,19
№4		544	760,96	681,6	2386,4

2. Кинематический анализ методом диаграмм

Метод кинематических диаграмм позволяет наглядно просмотреть, как изменяются перемещение, скорость и ускорение за цикл работы механизма.

Для построения диаграмм нам потребуется масштабный коэффициент угла поворота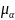

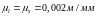
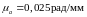
После масштабных коэффициентов приступаем к построению диаграмму перемещения точки В выходного звена в системе координат S(t). Для этого на оси абсцисс откладываем отрезок 0-12 равный 251.3мм. Затем делим отрезок 0-12 на две части, пропорционально углам рабочего и холостого (две равные части), далее делим отрезки 0-6 и 6-12 каждый на 6 равных частей и отмечаем точки 0,1,2...12. Проводим ординатные прямые через эти точки и на этих прямых с учетом выбранного масштаба откладываем перемещения точки B:

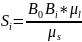(i = 0,1,2...12)

где 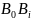- перемещение точки B. Соединив точки 0, 1,…, 12 плавной кривой, получим диаграмму перемещения точки B.

Диаграмма перемещений представлена на рис. 2.2.1

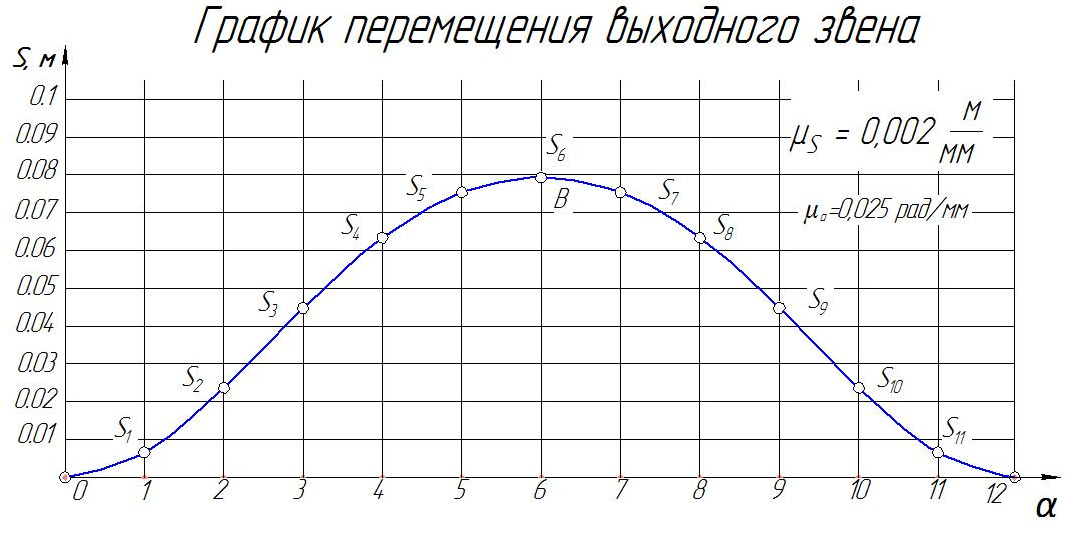
Рис 2.2.1. Диаграмма перемещения

Для построения диаграммы аналога скорости необходимо значения скоростей выходного звена (рассчитанные в пункте 2.1.2) поделить на угловую скорость исходного звена (кривошипа).

Примем масштабный коэффициент графика аналога скорости равным

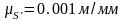
Отмечаем данные отрезки на графике и соединяем их плавной линией.

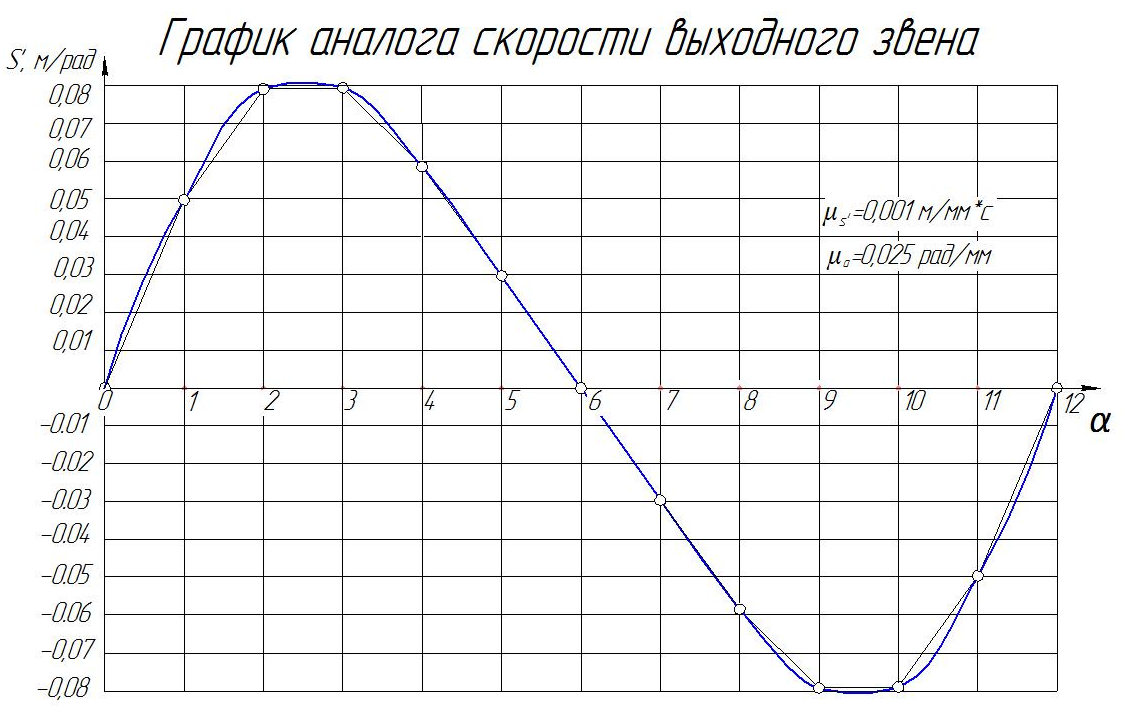
Рис. 2.2.2. График аналога скорости

График аналога ускорений строится методом графического дифференцирования. Для этого:

• график аналога скоростей аппроксимируем ломаной линией;

• с графика аналога скоростей ось абсцисс переносим на диаграмму аналога ускорений и продолжаем её за начало координат (влево);

• откладываем отрезок Н = 25 мм;

• на диаграмме аналога скоростей определяем точку 1^/, затем соединяем её с точкой О прямой линией:

• из точки Н проводим луч, параллельный хорде О1^/. Получаем точку 1^//;

• отрезок О1^// изображает средний аналог ускорения на временном интервале (0;1);

• чтобы найти точку диаграммы аналога ускорений необходимо из середины временного интервала (0;1) восстановить перпендикуляр и на этот перпендикуляр спроецировать точку 1­^//;

• эти построения повторяем для всего временного интервала.

Определим масштабный коэффициент диаграммы аналога ускорений:

;

.

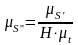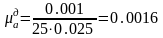
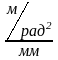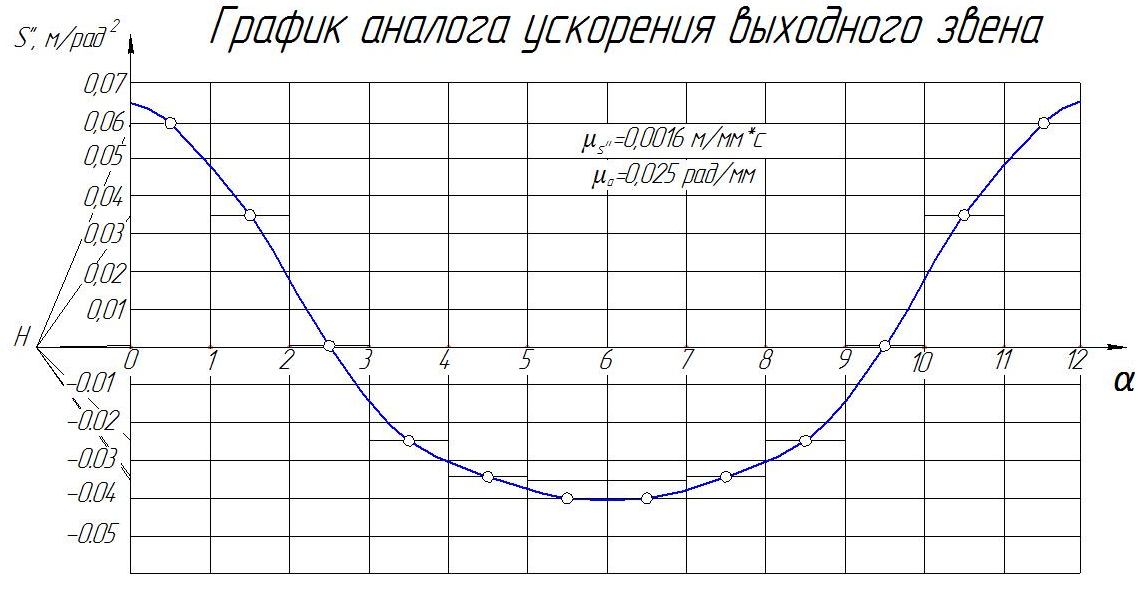
Рис. 2.2.3. Диаграмма аналога ускорений

Результаты кинематического анализа методом диаграмм приведем в табличной форме:

	0	1	2	3	4	5	6	7	8	9	10	11
аналог (м)	0,0644	0,048	0,018	0,0144	0,0304	0,0377	0,0407	0,0377	0,0304	0,0144	0,0177	0,048
ускорение (м/с)	1128,9	841,4	315,5	252,4	532,9	660,9	713,4	660,9	532,9	252,4	310,3	841,4

Расчет погрешности расчета ускорения выходного звена: