3.2 Спуск колонны

Н айдем результирующую силу при спуске колонны с ее вращением (рис. 5). Выходит аналогичный вывод формулы, за исключением того, что сила трения берется со знаком минус, т.к. она направлена в противоположную сторону от результирующей силы.

(8)

Очевидно, что без вращения

б

Рисунок 5

удет равен 1.

Как и в прошлый раз, введем функцию

как отношение результирующей

силы без вращения к результирующей

силе с вращением колонны.

Помимо качественной оценки влияния сил трения, отношение двух результирующих сил обезразмеревает величину, что дает наглядное представление отличия нагрузки колонны при подъеме или при спуске с вращением и без него. С помощью двух функций и можно построить графики, изменяя зенитные углы (град) и скорости вращения колонны (об/мин).

4 Построение графиков зависимостей для наклонного участка

Н

График 1

а графике 1 представлены зависимости функций W₁(n) при подъеме и W₂(n) при спуске колонны от частоты вращения при различных зенитных углах наклонного участка. Как видно из графика , при увеличении частоты вращения колонны функции монотонно убывают. Чем больше зенитный угол наклонного участка скважины , тем эффективней применять вращение. Так при подъеме колонны с вращением , с зенитным углом (по сути горизонтальная скважина), потенциальная нагрузка на крюке уменьшилась почти в половину.

Рассмотрим несколько подробнее поведение функций при спуске. Напомним, что представляет отношение при спуске колонны в скважину результирующей силы без вращения к результирующей силе с вращением. Когда производится спуск клонны, ей препятствует сила трения направленная против движения (рис. 5). При увеличении вращения колонны сила трения начнет уменьшаться, т.е. нагрузка на крюке увеличивается, а значит знаменатель в формуле (9) будет становиться больше по сравнению с числителем. Такая зависимость представленна, чтобы рассматривать изменения функций в пределах от 0 до 1, что облегчает сравнение показателей.

В первом разделе мы выяснили, что существует предельный угол наклонной плоскости при котором простейшая модель колонны находится находится в состоянии покоя. Воспользовавшись условием равновесия для вращающейся колонны можно найти предельные зенитные углы для разных коэффициентов трения при которых колонна перестанет свое движение в скважину. Условие равновесия:

Отсюда, (10)

Построим на основе формулы (10) графики для коэф-тов трения .

График 2

Очевидно, чем больше коэффициент трения, тем меньше предельный зенитный угол наклонного участка. Так, например, при (который мы использовали в предыдущих решениях), с увеличением частоты вращения колонны предельный угол растет примерно с до , т.е. до этих значений углов она будет опускаться под действием собственного веса.

5 Участок набора кривизны

Зная, как ведет себя модель колонны на наклонном участке, рассмотрим ее поведение на участке набора кривизны или, другими словами, на участке искривления скважины. В искривленном участке скважины, колонна находится в натянутом состоянии, большая часть ее веса приходиться на нижнюю стенку ствола, в результате чего возникают большие силы трения и сложные нагрузки.

В книге профессора А.Е. Сарояна подробно разбирается такой случай [8]. Остановимся на нахождении интересующей нас силы трения и веса колонны, обе они создают усилия в начале участка набора кривизны (рис. 6).

Д

Рисунок 6

анный участок задается рядом

определенных параметров:

– радиус искривления;

– вес 1 м бурильной колонны;

– зенитные углы в начале

и в конце участка;

– длина и угол элемента

колонны.

На элемент действует вес и усилие , возникающее в результате натяжения колонны касательными силами :

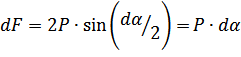, (11)

где при

В свою очередь, касательная сила определяется усилием и проекцией веса колонны на участке :

(12)

Определим силу нормального реакции на стенку скважины:

(13)

Как мы видим, в формуле присутствует усилие , найденное ранее. Подставим (12) в (11) и проинтегрируем :

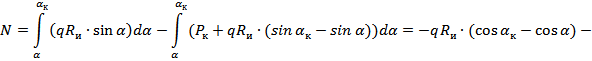
Так как сила трения по определению , то

, (14)

где (если рассматривать участок кривизны в целом, то полагаем )

– усилие с которой колонну тянут вниз (в нашем случаем это величина результирующей силы наклонного участка)

Часть собственного веса колонны найдем по формуле:

(15)

В итоге получим нагрузку на искривленном участке:

(16)

Стоит отметить следующее:

1) оба слагаемых берутся по модулю, поэтому в дальнейших расчетах необходимо рассматривать условие раскрытия скобок, в особенности это относится к силе трения;

2) знак относится к участку набора кривизны, знак – к участку спада.

3) разность углов тоже берется с модулем.

4) в зависимости от соотношения и колонна может быть прижата к нижней или к верхней части скважины, при зенитном угле при уже небольшой растягивающей нагрузке колонна прижимается к верхней стенке [].

При вращении колонны, как и в прошлый раз, осевая сила трения составляет проекцию главной силы трения через , тогда

, где (17)