6 Трехинтервальная скважина с тангенциальным профилем

О

Рисунок 7

стается приблизить нашу модель к реальному профилю скважины, которая состоит из трех участков (рис. 7): прямолиненого наклонного направленного участка, участка набора кривизны и вертикального участка, в котором на колонну будет действовать только собственный вес.

Для решения математической модели

необходимо ввести информацию о

скважине:

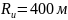– радиус искривления

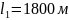– длина прямолинейного

наклонного участка

– длина вертикального участка

Параметры конструкции колонны:

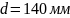– диаметр бурильной колонны

– вес 1 м БТ

( из справочных данных [2])

Технологические параметры:

– скорость подъема колонны из скважины (по нормативам [5])

– коэффициент трения.

Основными переменными являются: зенитный угол конечного наклонного участка скважины и частота вращения бурильной колонны .

Как и в прошлый раз, когда рассматривали влияние сил трения на наклонном участке скважины, построим графики зависимостей двух функций: и . Напомним, что это отношение суммы результирующих сил при подъеме колонны с вращением к сумме результирующих сил без вращения, а это отношение суммы результирующих сил при ее спуске без вращения к сумме сил с вращением колонны.

7 Построение графиков для трехинтервальной скважины

График 3

Из данного графика следует, что при подъеме колонны из скважины с зенитным углом поледнего наклонного участка , нагрузка на крюке уменьшиться на (в прошлый раз только на наклонном участке она уменьшилась почти в половину).

Наша математическая модель позволяет проводить различные вариации с параметрами, например, привести трехинтервальную скважину к наклонно направленной, обнулив длины вертикального участка и учатка набора кривизны.

Найдем предельные углы, когда колонна перестанет спускаться в скважину под действием собственного веса,т.е. наступит условие равновесия, для двух случаев: с вертикальным учатком и без него 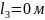. Условие равновесия наступит, когда нагрузка на крюке станет равна нулю:

(18)

Ч

График 4

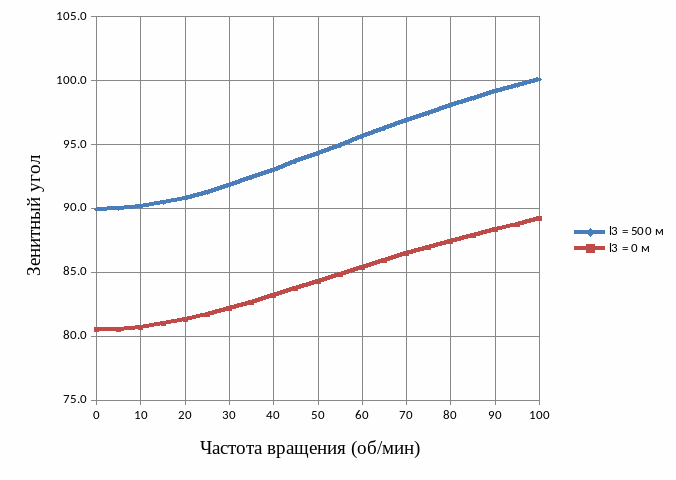тобы найти зависимость предельного зенитного угла последнего наклоного участка (град) от частоты вращения колонны воспользуемся методом Хорд. Этот метод позволяет найти решение нелинейного уравнения [6]. После нахождения углов можно посроить график.

Из графика следует, что при наличии вертикального участка , предельный угол составляет 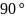и больше, это может объяснятся тем, что вес колонны превышает силу трения при спуске, и в теории такии трубы дойду до заданного интервала без принудительного проталкивания.

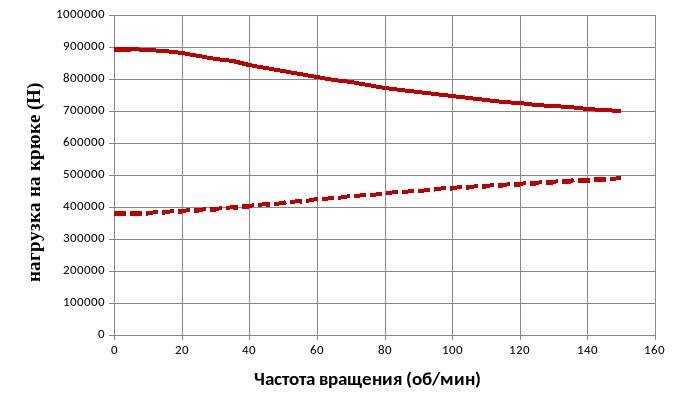
Диаграмма

Еще одним методом учета сил трения является, так называемый, «Фрикшен тест». Тест заключается в спуске и подъеме инструмента и снятии показаний с индикатора веса, что можно делать как с вращением, так и без вращения. Это очень простой способ для реализации в течение процесса бурения. Так представленная диаграмма характеризует нагрузку на крюке потенциальной трехинтервальной тангенциальной скважины.

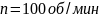При спуске и подъеме колонны в зависимости от ее частоты вращения, при зенитном угле разность нагрузки на крюке при подъеме колонны с вращением (допустим ) к нагрузке на крюке без вращения составит .