2 Инструменты для измерения расстояний и углов

Для измерения по карте линейных величин применяются изме­рительные линейки, циркули-измерители, курвиметр.

Измерительные линейки служат для проведения прямых линий, откладывания и измерения длин на бумаге. По краю измеритель­ных линеек расположена шкала миллиметровых делений. Величи­на делений шкалы измерительных линеек бывает и менее милли­метра, например, полмиллиметра и даже пятая часть миллиметра, как на особой линейке, называемой женевской. Величина одного деления шкалы называется ценой деления линейки.

Линейки изготовляют из дерева, металла, целлулоида и других материалов. Линейки часто делают гибкими. Перед употреблени­ем линейку необходимо проверить. Проверки измерительной ли­нейки заключаются в следующем:

1. Линейка должна плотно прилегать к гладкой плоской доске. Для проверки линейку кладут испытуемой поверхностью на глад-­ кую плоскую доску. Если между доской и линейкой не будет про­ светов, то линейка удовлетворяет указанному требованию.

Наличие просветов между доской и линейкой укажет на непра­вильность линейки. Такая линейка не годится для работы.

2. Ребра линейки должны быть прямыми линиями. Это проверяется таким образом. По испытуемому ребру линейки тонко очи­нённым карандашом проводят на бумаге линию АВ.

Затем линейку прикладывают к линии тем же ребром, но с другой стороны и вновь прочерчивают линию. Если эта линия совпадет с линией АВ, то проверяемое ребро представляет прямую. При кривизне испытуе­мого ребра получаются две линии.

В таком же порядке проверяется и второе ребро линейки.

В правильности каждого ребра линейки можно еще убедиться. глядя на него вдоль линейки. В этом случае глаз легко замечает малейшие искривления ребра. Линейка с кривыми ребрами не го­дится для работы.

3. Край линейки, на котором нанесена шкала, должен быть тонким (острым). Для проверки проводят на бумаге гонкую черту и на нее накладывают линейку так, чтобы черта была перпендику­лярна к ребру линейки и совпадала с каким-либо ее штрихом. За­ тем смещают несколько раз то в одну, то в другую сторону. Если при этом штрих линейки не будет сходить с черты, то условие вы­полнено. В противном случае будет наблюдаться смещение штри­хов. Если параллакс будет небольшой, то линейкой можно пользо­ваться, но при этом надо держать глаз строго по направлению штриха, по которому делается отсчет. При большом параллаксе линейка годна лишь для грубых измерений.

3. Общая длина шкалы измерительной линейки и величина ее делений должны быть верны. Это проверяют с помощью очень точной металлической линейки, которая не употребляется для ра­боты и называется нормальной. Сравнение рабочей линейки с нор­мальной называется компилированием.

Точность отсчета по шкале линейки. Допустим, что мы имеем измерительную линейку с миллиметровыми делениями, которые идут слева направо (рис. 7.1). Нужно сделать отсчет по указателю 0. В первую очередь устанавливают число целых делений линейки, идущих слева до указателя.

В нашем примере таких делений будет девять. Затем определя­ют на глаз левую часть деления, идущего непосредственно за по­следним целым делением отсчета. Эту часть в данном случае мож­но принять за 0,3 мм. После этого суммируют ее с целыми делениями и получают полный отсчет. В нашем примере он равен 9,3 мм.

В отсчет всегда входит систематическая ошибка за толщину штрихов. Очевидно, чем толщина штрихов меньше, тем точнее можно сделать отсчет. Однако при разных положениях указателя «О» ошибка за толщину штрихов будет различной. В частности, если

Рис. 7.1 Отсчет на шкале по указателю

указатель «0» находится в середине деления линейки, то эта ошибка равна нулю; от середины к краям она возрастает. Хотя отсчеты по миллиметровой шкале с толщиной штрихов 0,1 мм делаются до 0,1 мм, но действительная точность отсчитывания будет ниже.

При отсчитывании по шкале большое значение имеет разреша­ющая способность глаза, или критический угол зрения. Расстояние наилучшего зрения для нормального глаза 25 см. На этом расстоя­нии белая полоска будет различаться невооруженным глазом при ее ширине 0,1 мм. Эта величина представляет предельную точ­ность, с которой могут выполняться графические построения на бумаге.

Несовмещение черных штрихов, которые противостоят друг другу, ощущается глазом острее, и расхождение их можно оцени­вать с точностью, вдвое большей, чем разрешающая способность глаза.

Измерение длин линейкой. При проведении по линейке прямой, проходящей, например, через две точки, необходимо соблюдать ряд требований. Во-первых, точки должны быть четкие и малого размера. Во-вторых, диаметр точки не должен быть больше 0,1 мм. В-третьих, линия должна проводиться тонко очинённым каранда­шом с сохранением одного и того же наклона.

Измерение прямых линий производится двумя способами. При первом способе нулевой штрих линейки точно совмещается с ле­вым концом линии, а по правому ее концу делают отсчет на ли­нейке. Этот отсчет и будет представлять длину линии. При втором способе линейку прикладывают к линии, не совмещая нулевой штрих с левым концом последней, и делают отсчеты на линейке по обоим концам линии. Разность отсчетов даст длину линии. В этом случае измерение линии делается несколько раз.

Средняя квадратическая ошибка одного измерения

Средняя квадратическая ошибка арифметической средины

Таким образом, второй способ измерения линий линейкой имеет перед первым способом ряд преимуществ. Во-первых, он обеспечивает надежный контроль измерений, во-вторых, повы­шает их точность и, в-третьих, дает возможность сравнивать меж­ду собой результаты измерений и определять их точность.

Циркуль-измеритель предназначен для измерения прямых, из­вилистых и ломаных линий. Он состоит из двух стальных ножек, соединенных шарниром с винтами (рис. 7. 2). Концы ножек имеют гнезда для игл. Иглы закреплены в гнездах винтами. Этот циркуль служит для отложения линий данной длины и измерения расстоя­ний на планах и картах.

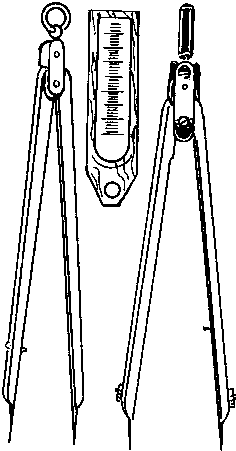
Циркуль-измеритель должен удовлетворять следующим усло­виям:

1. Ножки циркуля должны вращаться на шарнире плавно, и за­ данный им раствор не должен изменяться произвольно. Если цир­куль не удовлетворяет этому условию, то нужно ослабить или за­ крепить винты шарнира ножек.

1. Ножки циркуля должны быть одинаковой длины. Длина но­жек регулируется винтами, которыми закреплены иглы в гнездах ножек. Рис. 7.2 Циркуль измеритель

3. Иглы ножек циркуля должны быть достаточно острыми. В случае не­ соблюдения этого условия иглы необ­ходимо заострить.

При работе циркуль нужно держать в плоскости, перпендикулярной к плос­кости чертежа. Раствор ножек циркуля не следует делать более чем на прямой угол, которому соответствует расстоя­ние 15—18 см. Для проведения окруж­ностей и дуг, радиус которых превышает указанную величину, составную ножку циркуля удлиняют с помощью особой вставки, называемой удлинителем.

Линии значительной длины, а также извилистые и ломаные простым цирку­лем можно измерить и отложить только по частям.

Для этого устанавливают по линейке раствор циркуля, соответствующий ка­кому-нибудь целому числу километров или сотен метров, и таким шагом проходят вдоль измеряемой линии, ведя счет перестановок ножек. Порядок измерения показан на рис.4.3, а, где АР— измеряемая линия, А, В, С, О, Е, Г — места постановки ножек, ЕР — остаток. измеряемый по линейке. Стрелками показано направление пере­мещения ножек.

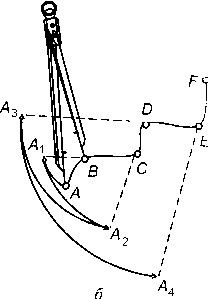
Рис. 7.3 Схемы измерения ломаных линий:

а — с плавными закруглениями; б — с резкими поворотами

Величину шага выбирают в зависимости от извилистости линии: от 4 см — при измерении кривых с плавными закруглениями, до 2 см — при измерении линий с большим числом резких поворотов. Последние более удобно изме­рять так, как показано на рис. 2.5, б. Ломаная ли­ния АВСОЕГ равна по длине конечному раствору циркуля А₄Г, величину которого определяют но масштабной линейке.

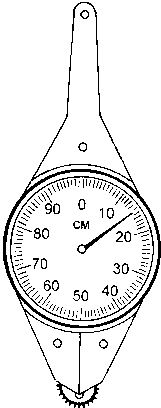
При измерении значительных по длине ло­маных и извилистых линий используют специальный прибор — курвиметр (рис. 7.4).

Механизм этого прибора состоит из измери­тельного колесика, соединенного системой зуб­чатых передач со стрелкой, которая движется по циферблату. При движении колесика вдоль из­меряемой по карте или плану линии стрелка пе­редвигается по циферблату и указывает пройденное колесиком расстояние в сантиметрах.

Для измерения расстояния следует предварительно вращением колесика установить стрелку курвиметра в

Рис. 7.4 Курвиметр начальное положение, то есть на отсчет 0. Затем

прокатить курвиметр вдоль из­меряемой линии от начала до конца, следя тем, чтобы стрелка двигалась по циферблату в направлении чисел 10, 20, 30 и так далее, и снять отсчет. Это и будет длина линии в сантиметрах.

Линию измеряют 3—4 раза. За окончательное значение берется нее арифметическое из наиболее близких результатов. Умножив величину масштаба карты на показание стрелки курвиметра. получают расстояние на местности.

При обводе линии курвиметр необходимо держать вертикаль­но причем движение колесика должно быть плавным, без сколь­жения и направлено касательно к кривой.

Перед работой курвиметр должен быть проверен. Проверка вы­полняется прогоном колесика по прямой длиной 20 см.

Точность измерения линий курвиметром в среднем равна 1/50. При коротких линиях эта точность снижается в два раза и более.

Инструменты для измерения углов

Угловые величины по карте измеряют с помощью транспорти­ра, хордоугломера, артиллерийского круга.

Транспортиром называется инструмент, который служит для из­мерения и построения углов на плоскости. Транспортиры изготав­ливают из металла, целлулоида и других материалов. Транспортир представляет полукруг, наглухо соединенный с линейкой. Внешний край полукруга скошен, и на нем нанесены деления, цена которых равна 1 или 1/2° и редко 1/4°. Центр полу­круга, находящийся на внутреннем крае линейки, отмечен штри­хом 0. Деления на полукруге идут от 0 до 180° по ходу часовой стрелки, а иногда от двух диаметрально противоположных нулей до 90° по ходу и против хода часовой стрелки.

Встречаются надписи от двух нулей до 180° (по внутреннему и внешнему краям полукруга). Диаметр транспортира, проходящий через 0 и 180°, называется нулевым, а радиус, идущий через деле­ние 90°, называется средним.

У некоторых транспортиров с нулевым диаметром совмещается наружное ребро линейки, на котором отмечен центр полукруга и нанесена миллиметровая шкала. Бывают также круглые транспор­тиры, деления которых идут от 0 до 360° в обе стороны. Диаметр транспортира изменяется от 6 до 20 см. Транспортир должен удовлетворять следующим требованиям:

1. Деления транспортира должны быть верны. Они наносятся делительными машинами автоматически и с большой точностью, а поэтому они обычно равны. Чтобы убедиться в этом, достаточно все деления осмот­реть в лупу. Если окажется, что деле­ния транспортира неодинаковы, то он не годен для работы.

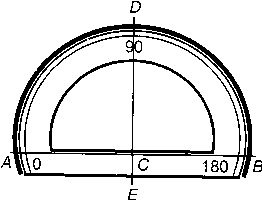
Рис. 7.5 Транспортир

Проверка правильности положения центра транспортира

2. Центр транспортира должен на­ходиться точно в середине нулевого диаметра. Для проверки этого с по­мощью линейки Дробышева или штангенциркуля строят две взаимно перпендикулярные прямые и при­кладывают транспортир к этим ли­ниям таким образом, чтобы нулевой диаметр совместился с одной из них, а штрих с надписью 90 — с другой (рис. 7.5). По внутреннему краю линейки транспортира проводят тонкую линию. Если эта линия совпадет с данной пря­мой, то центр транспортира лежит на нулевом диаметре. Вместе с этим устанавливают, находится ли центр транспортира на второй данной прямой.

В положительном случае средний радиус перпендикулярен к нулевому диаметру, то есть центр транспортира находится точно в середине этого диаметра.

Если транспортир не удовлетворяет второму требованию, то в таком случае транспортир имеет эксцентриситет. Этот недостаток не может быть устранен. В том случае, когда влияние эксцентри­ситета на точность отсчета будет не более 15', транспортиром мож­но работать.

2. Наружное ребро линейки транспортира должно быть парал­лельно нулевому диаметру. Чтобы проверить это требование, прочерчивают на бумаге прямую линию и прикладывают к ней транспортир нулевым диаметром. К наружному краю линейки транспортира прикладывают гипотенузой треугольник, а к катету последнего — линейку. Затем транспортир убира­ют, а треугольник передви­гают вдоль линейки. Если при этом передвижении ги­потенуза треугольника со­ вместится с прочерченной прямой, то транспортир удовлетворяет указанному требованию. В противном случае гипотенуза треугольника образует с прочерченной линией некоторый угол BC₁ D₁.

В направления, построенные таким транспортиром с использованием наружного края его линейки, будет входить систематическая ошибка, равная углу BC₁ D₁ . Эта ошибка может быть направлена то в одну, то в другую сторону в зависимости от положения транспортира. При построении угла этим транспортиром ошибка в одних положениях последнего войдет в величину угла в двой­ном размере, а при других положениях может совсем не сказаться.

Хордоугломер представляет собой специальный график, награ­вированный на металлической пластине в виде поперечного мас­штаба, предназначенного для измерения углов по длинам соответ­ствующих им хорд (рис. 4.6). В основе построения графика лежит известная зависимость между радиусом окружности R, централь­ным углом а и длиной хорды t:

Если радиусу окружности придать постоянное значение (на хордоугломере оно обычно равно 12 см), то величины хорд будут пропорциональны только синусам стягиваемых ими углов. Так как при угле 60° длина хорды равна радиусу, то угол 10-00 принят за единицу при расчете хордоугломера.

На верхней горизонтальной шкале хордоугломера подписаны величины хорд, соответствующие углам от 0-00 до 15-00 через каждые 20 малых делений (от 0 до 20). У концов хорд, соответст­вующих углам 1-00, 2-00 и так далее до 15-00, подписаны числа 1, 2 ... 15.

Число 10, отвечающее углу 10-00, хорда которого равна радиу­су, обведено кружком. Каждое большое деление на верхней линии графика разделено на пять малых делений ценой 0-20, которые подписаны цифрами 2, 4, 6 и 8, что соответствует 0-20, 0-40, 0-60 и 0-80. Слева по вертикали графика по концам четных горизонталь­ных линий подписаны числа 2, 4, 6 ... 18, соответствующие 0-02, 0-04,0-06... 0-18.

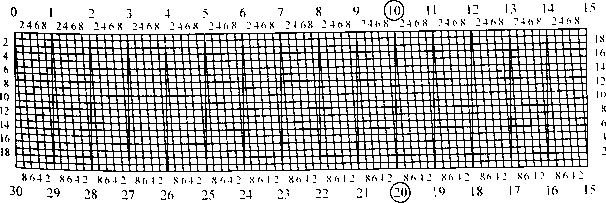
Рис. 7.6 Хордоугломер

Оцифровка делений на нижней горизонтальной и правой вертикальной шкалах сделана для определения длин хорд при построении дополнительных до 30-00 углов.

На обратной стороне пластины нанесены два поперечных мас­штаба — верхний для работы на картах масштаба 1:50 000, его основание 2 см, что соответствует 1 км на местности; нижний — для работы на картах масштаба 1:25 000, его основание 4 см. что соответствует 1 км на местности.

Артиллерийский круг АК-3 вместе с масштабно-прицельной ли­нейкой МПЛ-25 или МПЛ-50 представляет собой комбинирован­ный прибор для измерения линейных и угловых величин (рис. 4.7) и предназначен для построения и измерения углов и расстояний на карте (планшете). Артиллерийский круг АК-3 пред­ставляет собой целлулоидную пластину диаметром 22 см с двумя срезанными сегментами. По внешнему срезу круга нанесена угло­мерная шкала с ценой деления 0-10. Большие деления ценой 1-00 оцифрованы двумя рядами цифр. Наружный ряд цифр (черного цвета)

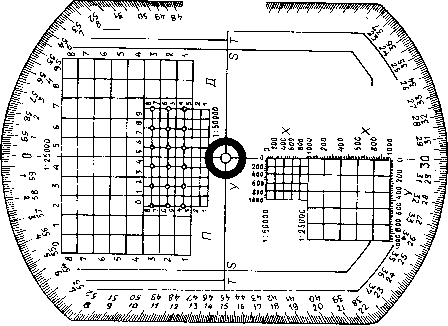
Рис. 7.7 Артиллерийский круг АК-3

нанесен против хода часовой стрелки, внутренний (красного цвета) — по ходу часовой стрелки.

На верхней половине круга нанесены через 0,5 см линии крае-го цвета, параллельные диаметру 30-00, используемые для ориентирования круга. Кроме того, круг имеет две мерки — 1:25 000 и 1:50 000, расположенные в нижней части круга; шкалы мерок оцифрованы через 200 м, цена деления шкал мерки 1:25 000 равна 10 м, мерки 1:50 000 — 50 м; обе мерки смещены от центра круга вниз (по оси Х) на 1 км в соответствующем масштабе, что позволя­ет непосредственно устанавливать центр круга по заданным коор­динатам (определять координаты точки, на которую наложен центр круга).

В центре круга укреплена латунная втулка для соединения кру­га с масштабно-прицельной линейкой.