3 Методы изображения земной поверхности на плоскости

Изучение больших участков земной поверхности ведется по уменьшенным ее изображениям. Поверхность Земли в целом на­глядно и в подобном виде можно изобразить лишь на ее модели — глобусе. Однако размеры глобусов не позволяют подробно изобра­зить земную поверхность.

Например, если изобразить Землю с уменьшением в 1 000 000раз, то радиус глобуса будет равен 6,37м. Тем не менее точность столь огромного глобуса будет недоста­точной для военных целей, а из-за размеров такой глобус будет непригоден к использо­ванию.

В силу этого подробные изображения земной поверхности в целом и по частям производятся на плоскости.

Так как физическая поверхность Земли имеет неправильную форму, то на плоскости изображают не действительные очертания этой поверхности, а проекции их на уровенную поверхность (как известно, вместо уровенной поверхности, которая не определяет­ся математически, берется поверхность эллипсоида). Таким обра­зом, изображение земной поверхности на плоскости представляет собой процесс двойного проектирования. Вначале земную поверх­ность проектируют на теоретически рассчитанную поверхность эллипсоида с помощью нормалей к его поверхности, а затем по определенным математическим законам эти проекции переносят на плоскость (рис. 8.5).

Как будет доказано далее, при изображении небольшого участ­ка местности соответствующую ему часть уровенной поверхности можно принять за горизонтальную плоскость. В этом случае точки физической поверхности Земли проектируются перпендикуляра­ми, параллельными друг другу, на горизонтальную плоскость Р (рис. 8.6). Пересечение перпендикуляров с плоскостью /'дает точ­ки а, b, с, d, являющиеся ортогональными проекциями точек зем­ной поверхности А, В, С, D на горизонтальную плоскость. Полу­ченный плоский четырехугольник аbсd представляет собой горизонтальную проекцию пространственного четырехугольника АВСD физической поверхности Земли. Линии аb, bс, cd, dа называются горизонтальными проложениями линий AB, BC,

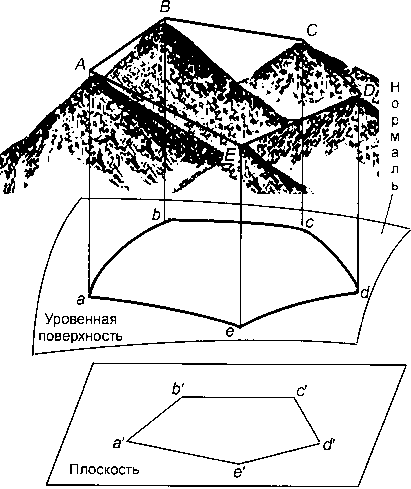
Рис. 8.5 Проектирование объектов поверхности Земли на

эллипсоид и плоскость

CD, DA местности, а углы между ними β₁ , β₂, β ₃, β ₄ — горизонтальными уг­лами.

В общем случае фигура аbсdна плоскости не будет подобна участку местности АВСD, а горизонтальные проложения линий не равны самим линиям местности.

Например, dс=DС₁ = DС сох v, где v — угол наклона местности, то есть угол, об­разованный наклонной линией с горизонтальной плоскостью (рис. 6.6).

Следовательно, для изображения участка местности на гори­зонтальной плоскости следует знать горизонтальные проложения ее сторон и горизонтальные углы между сторонами. Таким обра­зом, горизонтальную проекцию участка АВСD можно изобразить на плоскости в уменьшенном и подобном виде.

Рассмотрим, при каких размерах участков земной поверхности можно не считаться с кривизной Земли.

Пусть АВ - часть уровенной поверхности Земли, принимаемой за сферу с центром 0 радиусом R . Дуга АВ = S (рис. 8.7). Заменим участок сферической поверхности Земли плоскостью, касающейся сферы в точке А.

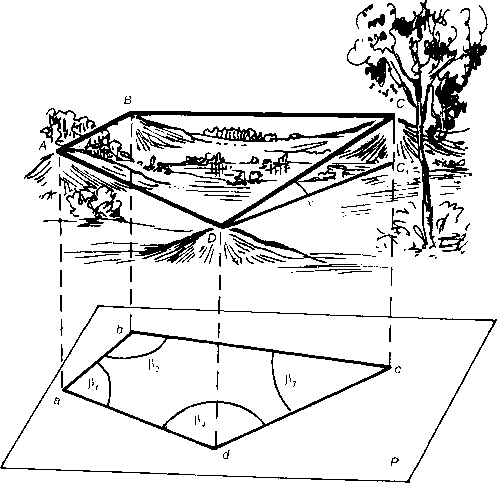
Рис. 8.6 Горизонтальная проекция участка земной поверхности

Для учета искажения расстояния между двумя точками при за­мене сферической поверхности плоскостью определим разность между длиной касательной АВ'=d и дуги АВ = S, то есть ΔS=d-S. Как следует из рис. 3.7, S=Rε, где значение ε выраже­но в радианной мере, d = Rtgε.

Тогда ΔS= Rtgε – Rε= R(tgε - ε). Разложив tgε в ряд и ограни­чиваясь при этом двумя членами разложения, получим tgε= tgε+ε ³ /3. Тогда ΔS= R(ε + ε³ /3-ε)=R ε³/3 . Полагая ε=S/R, имеем ΔS=S³ /3R ².

Замена участка земной поверхности радиусом 10 км плоско­стью влечет за собой незначительные (менее 1:1 000 000) искажения расстояний, которые допустимы при самых точных линейных измерениях.

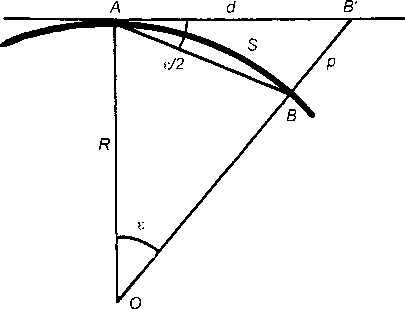
Рис. 8.7 Зависимость расстояний и высот точек от кривизны Земли

Изображение на плоскости в уменьшенном и подобном виде горизонтальной проекции небольшого участка земной поверхно­сти, который можно принять за плоский, называется планом этого участка. Степень уменьшения горизонтальных проекций линий местности при изображении их на плане или карте называется масштабом.

Принято считать, что план можно составлять на территорию, не превышающую площади круга с радиусом 11 км. При решении ин­женерных задач за плоскость можно принимать участок уровенной поверхности радиусом до 25 км, так как при этом искажения длин линий будут достаточно малы (порядка 1:200 000). Части земной поверхности больших размеров нельзя принять за плоские. Умень­шенное изображение каждой из них на плоскости носит условный характер и сопровождается значительными искажениями.

Для полной характеристики участка физической поверхности Земли помимо горизонтальной проекции этого участка необходи­мо еще знать высоты его точек над уровенной поверхностью.

Высоты бывают нормальные (абсолютные), если их отсчет ве­дется от уровенной поверхности Земли, и условные (относитель­ные), если их отсчет ведется от произвольной поверхности, парал­лельной уровенной поверхности Земли. Началом счета нормаль­ных высот служит квазигеоид, который незначительно отступает °т геоида. На поверхности океанов квазигеоид и геоид совпадают. На 90 % земной поверхности квазигеоид отходит от геоида всего на несколько миллиметров, в горной местности на несколько де­циметров и лишь в отдельных точках квазигеоид отходит от геоида на 2 м. Так как поверхности геоида и квазигеоида практически совпадают, то высоты точек местности измеряются от среднего уровня поверхности моря.

По топографической карте определяют нормальные высоты то­чек местности.

При замене участка АВ (рис. 8.7) уровенной поверхности Земли касательной АВ' точка В перемещается в положение В', в связи с чем ее высота изменяется на величину р. Величина р выражает влияние кривизны Земли на высоты точек и называется поправ­кой за кривизну Земли.

Как следует из рис. 3.7, угол ВАВ' = ε/2 как угол, составленный касательной и хордой. По малости этого угла отрезок/? можно рас­сматривать как дугу радиуса S, то есть р = Sε/2. Поскольку ε = S/R то р = S²/2R. Придавая S различные численные значения при R = 6371 км, определим соответствующие величины поправок p.

Отсюда следует, что влияние кривизны Земли на высоты точек существенно сказывается уже при расстоянии между ними 0,3 км. Следовательно, при измерении высот нельзя пренебрегать кри­визной Земли даже при небольших горизонтальных расстояниях между точками.

Простейшим прибором для измерения уровня воды является футшток — рейка с делениями, установленная вертикально по от­весу и прочно укрепленная на скале или каком-то береговом соо­ружении так, чтобы нижний конец был погружен в воду. Высоту уровня воды отсчитывают по рейке с точностью до 1 см. Уровень моря испытывает постоянные колебания, связанные с целым ком­плексом причин: приливы и отливы, атмосферное давление, ве­тер, осадки, материковый сток воды.

Например, наивысший уровень Балтийского моря 313 см выше нуля наблюдался в сентябре 1924 г., а наименьший уровень 153 см ниже нуля — в ноябре 1890 г.

В России за начало отсчета нормальных (абсолютных) высот принят нуль Кронштадтского футштока (горизонтальная черта на медной пластинке, замурованной в гранитный устой Обводного канала; пластинка закрыта сверху специальной защитной планкой с надписью: «Исходный пункт нивелирной сети СССР»), соответ­ствующий среднему уровню Балтийского моря по данным много­летних наблюдений. Поэтому система высот в нашей стране полу­чила название Балтийской.

Высоты пунктов нивелирной сети являются нормальными вы­сотами и служат исходной высотной основой при топографиче­ской съемке рельефа, изображаемого на топографических картах.

Вопросы для самопроверки

1. Что представляет собой наша Земля и зачем необходимо уточнять ее размеры?

2. Какие основные параметры характеризуют фигуру Земли'?

2. Какая поверхность наиболее точно отображает физическую поверхность Земли и что принимается в качестве математической поверхности Земли?

4. В чем отличие референц-эллипсоида от земного эллипсоида?

4. Какие участки земной поверхности можно принимать за плоскость и почему?

6. Какие измерения используются для установления фигуры Земли?

7. Каково назначение государственной геодезической сети, каковы принципы ее построения?

7. Какие вы знаете методы изображения земной поверхности на плос­кости?

7. Что называется масштабом?

10. Что такое футшток?

10. Что в России принято за начало отсчета нормальных (абсолютных)высот?