Дифференциальное исчисление функции одной независимой переменной

161. Задание {{ 4 }} Дифф_од_№1

Производная второго порядка функции y=cos3x имеет вид

 9cos3x

 -9cos3x

 -9sin3x

 9sin3x

162. Задание {{ 11 }} Дифф_од_№2

Касательная к графику функции y=f(x) проходит через начало координат и точку А(-4;-24). Тогда значение f`(-4)(производная f(x) в -4) равно

Правильные варианты ответа: 6;

163. Задание {{ 12 }} Дифф_од_№3

Закон движения материальной точки имеет вид x(t)=7+5t², где x(t) – координата точки в момент времени t. Тогда скорость точки при t=1 равна

 10

 9

 8

 11

164. Задание {{ 13 }} Дифф_од_№4

Приращение y функции y=-x² при изменении значения аргумента от -2 до 3 равно

 5

 3

 -2

 -5

165. Задание {{ 208 }} Дифф_од_№6









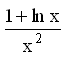
166. Задание {{ 26 }} Дифф_од_№7

Установите правильное соответствие между функцией и ее производной

167. Задание {{ 27 }} Дифф_од_№8

Производная произведения равна ...









168. Задание {{ 31 }} Дифф_од_№9

Производная второго порядка функции имеет вид…









169. Задание {{ 145 }} Дифф_од_№10









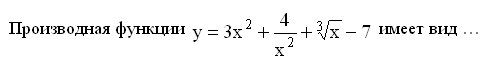
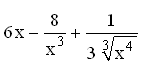
170. Задание {{ 146 }} Дифф_од_№11









171. Задание {{ 204 }} Дифф_од_№5









172. Задание {{ 310 }} Дифф_од_№12

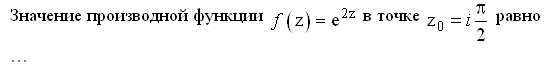
 1

 -1

 2

 -2

173. Задание {{ 395 }} Дифф_од_№13

 0

 1

 2

 3

174. Задание {{ 404 }} Дифф_од_№14









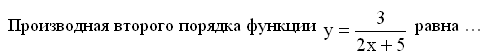
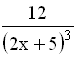
175. Задание {{ 405 }} Дифф_од_№15

 1

 2

 3

 4

Дифференциальные уравнения

176. Задание {{ 19 }} Д_ур_№1

Порядок дифференциального уравнения равен ...

 2

 3

 1

 4

177. Задание {{ 21 }} Д_ур_№2

Дано дифференциальное уравнение . Тогда соответствующее характеристическое уравнение имеет вид ...









178. Задание {{ 22 }} Д_ур_№3

Установите соответствие между дифференциальным уравнением и его характеристическим уравнением ...

179. Задание {{ 190 }} Д_ур_№4









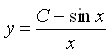
180. Задание {{ 191 }} Д_ур_№5









181. Задание {{ 192 }} Д_ур_№6









182. Задание {{ 193 }} Д_ур_№7









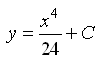
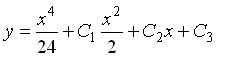
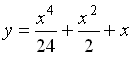
183. Задание {{ 238 }} Д_ур_№8









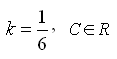
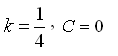
184. Задание {{ 239 }} Д_ур_№9









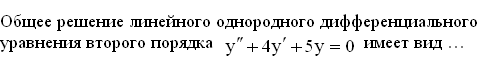
185. Задание {{ 240 }} Д_ур_№10









186. Задание {{ 268 }} Д_ур_№11









187. Задание {{ 269 }} Д_ур_№12









188. Задание {{ 274 }} Д_ур_№13

График всякого решения дифференциального уравнения второго порядка называется ? кривой. (Вместо - ? вставьте нужное слово)

Правильные варианты ответа: интегральной;

189. Задание {{ 275 }} Д_ур_№14

Если свободный член , то уравнение

называется линейным ? уравнением. (Вместо - ? вставьте нужное слово)

Правильные варианты ответа: однородным;

190. Задание {{ 276 }} Д_ур_№15

Если свободный член , то уравнение

называется линейным ? уравнением. (Вместо - ? вставьте нужное слово)

Правильные варианты ответа: неоднородным;