Прямая линия на плоскости
29. Задание {{ 60 }} Пря_№1
Точка (2;3) лежит на прямой с уравнением
x-4y+10=0
y=3x-3
y=-2x+5
4x-2y+3=0
30. Задание {{ 61 }} Пря_№2
Произведение угловых коэффициентов прямых 2x-3y-9=0, 9x-y+15=0 равно ...
Правильные варианты ответа: 6;
31. Задание {{ 138 }} Пря_№9
Даны точки А(-7;3) и В(3;5). Тогда сумма координат середины отрезка АВ равна
Правильные варианты ответа: 2;
32. Задание {{ 132 }} Пря_№3
Расстояние от точки M(2;-1) до прямой 3x+4y-22=0 равно...
Правильные варианты ответа: 4;
33. Задание {{ 133 }} Пря_№4
Формула - расстояние от точки до прямой имеет вид ...
34. Задание {{ 134 }} Пря_№5
Условием перпендикулярности прямых является равенство k1k2=
1
-1
0
2
35. Задание {{ 135 }} Пря_№6
Лежит ли точка K(-2;1) на линии 2x+y+3=0 ?
Да
Нет
36. Задание {{ 136 }} Пря_№7
Лежит ли точка L(1;1) на линии 2x+y+3=0 ?
Да
Нет
37. Задание {{ 137 }} Пря_№8
Общее уравнение прямой имеет вид ...
38. Задание {{ 201 }} Пря_№11
16
14
4
3
39. Задание {{ 181 }} Пря_№10
40. Задание {{ 292 }} Пря_№13
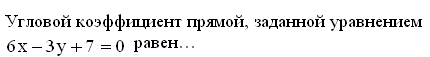
41. Задание {{ 295 }} Пря_№14
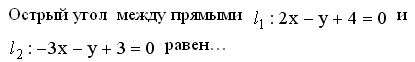
42. Задание {{ 316 }} Пря_№15
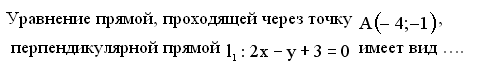
43. Задание {{ 270 }} Пря_№12
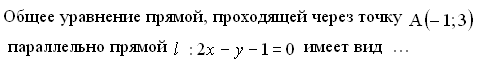
Ведение. Элементы теории множеств Множества и операции над ними
44. Задание {{ 50 }} Мно_№1
Множество A – множество всех девушек, студенток НГМУ.
Множество B – множество всех, обучающихся на 2-м курсе НГМУ
Выберите верное(ые)
словесное(ые) описание(ия) множества С,
определяемого равенством С=
Второкурсники (только юноши)
Все девушки - студентки НГМУ, кроме второкурсниц
Все юноши - студенты НГМУ, кроме второкурсников
Второкурсницы
45. Задание {{ 51 }} Мно_№2
Множество A - множество всех девушек, студенток НГМУ.
Множество B - множество всех, обучающихся на 2-м курсе НГМУ
Выберите верное(ые) словесное(ые) описание(ия) множества С, определяемого равенством С=А\В
Второкурсницы
Второкурсники (только юноши)
Все девушки-студентки НГМУ, кроме второкурсниц
Все второкурсники, второкурсницы и девушки с 1, 3, 4, 5 курсов
46. Задание {{ 52 }} Мно_№3
Множество A - множество всех девушек, студенток НГМУ.
Множество B - множество всех, обучающихся на 2-м курсе НГМУ
Выберите верное(ые) словесное(ые) описание(ия) множества С, определяемого равенством С=B\A
Второкурсницы
Все девушки - студентки НГМУ, кроме второкурсниц
Все юноши - студенты НГМУ, кроме второкурсников
Второкурсники (только юноши)
47. Задание {{ 53 }} Мно_№4
Множество A – множество всех девушек, студенток НГМУ.
Множество B – множество всех, обучающихся на 2-м курсе НГМУ
Выберите верное(ые)
словесное(ые) описание(ия) множества С,
определяемого равенством С=
Второкурсницы
Второкурсники (только юноши)
Все девушки -студентки НГМУ и второкурсники (юноши)
Все второкурсники, второкурсницы и девушки с 1, 3, 4, 5 курсов
48. Задание {{ 54 }} Мно_№5
Даны множества А
и В.
Тогда множество С,
изображенное на рисунке,
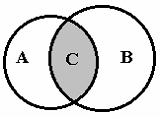есть…
49. Задание {{ 55 }} Мно_№6
Установить соответствия между списками двух множеств, заданных различным образом
|
|
|
|
|
|
|
|
50. Задание {{ 56 }} Мно_№7
Дано множество А={0;1;2;3;4;5}. Тогда несобственным подмножеством множества А является ...
{0;5}
{0;2;3;}
{0;1;2;3;4;5}
51. Задание {{ 112 }} Мно_№8
На рис. 1 изображены 2 множества: круг– множество А и прямоугольник – множество В.
На рис. 2 изображено множество D, полученное в качестве диаграммы Венна из множеств А и В.
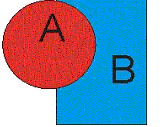рис.1
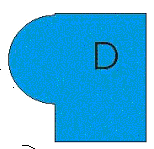рис.2
Какие утверждения из приведённых ниже верны (на цвет внимания не обращать!)?
D=А\В
D=B\A
D=АUВ
52. Задание {{ 115 }} Мно_№9
На рис. 1 изображены 2 множества: круг– множество А и прямоугольник – множество В.
На рис. 2 изображено множество E, полученное в качестве диаграммы Венна из множеств А и В.
рис.1
рис.2
Какие утверждения из приведённых ниже верны (на цвет внимания не обращать!)?
E=А\В
E=АUВ
E=B\A
E=А
В
53. Задание {{ 116 }} Мно_№10
На рис. 1 изображены 2 множества: круг– множество А и прямоугольник – множество В.
На рис. 2 изображено множество F, полученное в качестве диаграммы Венна из множеств А и В.
рис.1
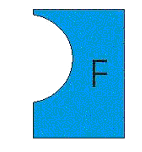рис.2
Какие утверждения из приведённых ниже верны (на цвет внимания не обращать!)?
F=B\A
F=АUВ
F=А В
F=А\В
54. Задание {{ 117 }} Мно_№11
На рис. 1 изображены 2 множества: круг– множество А и прямоугольник – множество В.
На рис. 2 изображено множество F, полученное в качестве диаграммы Венна из множеств А и В.
рис.1 рис.2
Какие утверждения из приведённых ниже верны (на цвет внимания не обращать!)?
F=A
F=B
55. Задание {{ 339 }} Мно_№13
Даны множества A=(-1;2];B=[1;4). Тогда B\A =
(2;4)
(2;4]
[2;4)
[2;4]
56. Задание {{ 340 }} Мно_№14
Равенство верно ?
Да
Нет
57. Задание {{ 341 }} Мно_№15
Даны множества A=(-1;2]; B=[1,4). Тогда A\B=
(-1;1)
(-1;1]
[-1;1)
[-1;1]
58. Задание {{ 307 }} Мно_№12
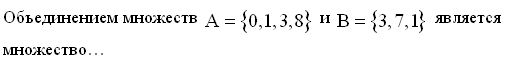
