Содержание тестовых материалов Аналитическая геометрия Кривые второго порядка

1. Задание {{ 139 }} Кри_№1

Среди уравнений кривых укажите уравнения гиперболы.

 (x+2)²-(y-1)²=16

 x+y²=9



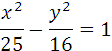
 3x²+y²=25

2. Задание {{ 140 }} Кри_№2

Уравнение 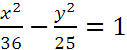на плоскости определяет

 гиперболу

 эллипс

 параболу

 пару прямых

3. Задание {{ 141 }} Кри_№3

Уравнение x+y²=9 на плоскости определяет

 гиперболу

 эллипс

 параболу

 пару прямых

4. Задание {{ 202 }} Кри_№4









5. Задание {{ 293 }} Кри_№7









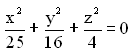
6. Задание {{ 296 }} Кри_№8









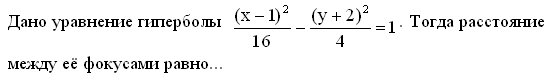
7. Задание {{ 243 }} Кри_№5









8. Задание {{ 399 }} Кри_№10

 A

 B

 C

 D

9. Задание {{ 403 }} Кри_№11









10. Задание {{ 413 }} Кри_№12









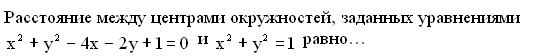
11. Задание {{ 271 }} Кри_№6









12. Задание {{ 421 }} Кри_№13









13. Задание {{ 427 }} Кри_№14









14. Задание {{ 320 }} Кри_№9









15. Задание {{ 478 }} Кри_№15

Уравнение окружности, диаметром которой служит отрезок AB, где A(4,-1), B(-4,5) выглядит ....

 x²+(y-2)²=25

 x²+(y+2)²=25

 x²-(y-2)²=25

 x²+(y-2)²=5

Прямая и плоскость в пространстве

16. Задание {{ 62 }} ПР_Пл_№1

Если плоскость Ax+By+5z-9=0 проходит через точку T(2;-2;3), то разность A-B коэффициентов равна ...

Правильные варианты ответа: -3;

17. Задание {{ 63 }} ПР_Пл_№2

Даны точки А(1;-3;4) и B(-1;-2;3). Тогда координаты точки М, симметричной точке В относительно точки А, равны ...

 (-3;-1;2)

 (3;-4;5)

 (-1;-3;2)

 (-4;3;5)

63. Задание {{ 203 }} ПР_Пл_№4









18. Задание {{ 207 }} ПР_Пл_№5









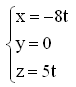
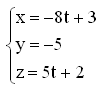
19. Задание {{ 182 }} ПР_Пл_№3

 A

 B

 C

 D

20. Задание {{ 343 }} ПР_Пл_№8









21. Задание {{ 297 }} ПР_Пл_№7









22. Задание {{ 479 }} ПР_Пл_№10

Уравнение плоскости, проходящей через точку A(3;-2;5) перпендикулярно ее радиус-вектору выглядит ...

 3x-2y+5z-38=0

 3x+2y+5z-38=0

 3x-2y+5z+38=0

 3x-2y-5z-38=0

23. Задание {{ 480 }} ПР_Пл_№11

Уравнение плоскости, проходящей через точку М(2;-1;3) и перпендикулярно плоскостям 2x+y-5z+4=0 и 3x-y+4z=0 выглядит ...

 x+23y+5z+6=0

 x-23y+5z+6=0

 x+23y-5z+6=0

 x+23y+5z-6=0

24. Задание {{ 481 }} ПР_Пл_№12

Расстояние точки M(5;-2;2) до плоскости 4x+y+3z-11=0 равно ...





 5

 0

25. Задание {{ 482 }} ПР_Пл_№13

Уравнение плоскости, проходящей через точку M(-1,2,3) и прямую L: выглядит …

 5x-6y+2z+11=0

 5x-6y-2z+11=0

 5x-6y+2z-11=0

 5x+6y+2z+11=0

26. Задание {{ 483 }} ПР_Пл_№14

Каноническое уравнение прямой, заданной общими уравнениями выглядит ….









27. Задание {{ 484 }} ПР_Пл_№15

Уравнение прямой, проходящей через точку M(1,-2,-3) перпендикулярно плоскости P: 3x-y+5z-1=0 выглядит ...











28. Задание {{ 272 }} ПР_Пл_№6









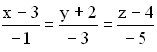
28. Задание {{ 422 }} ПР_Пл_№9







