3 Расчет шпонок
3.1 Расчет призматических шпонок
Соединения деталей механических передач в большинстве случае осуществляют с помощью призматических шпонок.
Размеры шпонки выбирают в зависимости от диаметра вала (таблица1). Длину шпонки l выбирают на 5…10 мм меньше длины ступицы из стандартного ряда: 6, 8 10, 12, 14, 16, 18, 20, 25, 32, 36, 40, 45, 50, 56, 63, 70, 80, 90.
Выбранную шпонку проверяют на смятие:
<
,
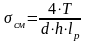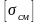где Т - крутящий момент на валу, Нмм;
d - диаметр вала, мм;
h - высота шпонки, мм (таблица 2);
lp-
рабочая длина шпонки, мм;
,
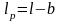b - ширина шпонки, мм (таблица 2);
- допускаемое напряжение смятия, = 110 МПа.
Если расчетное напряжение смятия будет значительно ниже допускаемого, можно взять шпонку на номер меньше и проверить ее. В случае если же оно превысит допускаемое, следует поставить две шпонки (под углом 1800).
3.2 Расчет сегментных шпонок
При небольших диаметрах сопряжений валов с деталями (до 38 мм) находят применение сегментные шпонки, характеризующиеся высокой технологичностью изготовления и удобством сборки. Вследствие снижения прочности вала за счет глубоких пазов сегментные шпонки применяют при передаче небольших крутящих моментов.
Сегментную шпонку проверяют на смятие, а соединение - на срез:
<
;
,
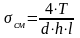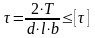где Т - крутящий момент на валу, Нмм;
d - диаметр вала, мм;
h - высота шпонки, мм (таблица 3);
l –длина шпонки, мм;
b - ширина шпонки, мм (таблица 3).
- допускаемое напряжение на срез, = 90 МПа.
Если прочность соединения окажется недостаточной, следует поставить по длине ступицы насаживаемой на вал детали две или даже три шпонки.
4 Примеры расчетов
4.1 Пример проектного расчета вала
Выполним расчет тихоходного вала конического редуктора на основании следующих известных данных: окружная сила на колесе Ft=1535 H; радиальная сила Fr=203 H; осевая сила Fa=520 H; средний делительный диаметр зубчатого колеса dm=240 мм; расстояния между линиями приложения нагрузок -а=0,06 м, с=0,155 м; крутящий момент на валу Т= 175 Нм.
На вал действуют вилы в двух взаимно перпендикулярных плоскостях, поэтому расчетные схемы будем рассматривать в горизонтальной и в вертикальной плоскости (рисунок 5).
Рисунок 5. Эпюры изгибающих и крутящих моментов на валу
а) Определим реакции опор в горизонтальной плоскости (для данной расчетной схемы учитываем только окружную силу и одну реакцию опоры).
Условие равновесия относительно точки А:
;
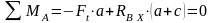отсюда
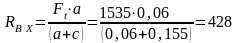Н;
Условие равновесия относительно точки В:
;
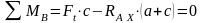отсюда
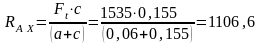Н;
Проверка:
.
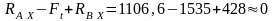б) Определим реакции опор в вертикальной плоскости (учитываем осевую и радиальную силу, а также реакцию опоры).
Условие равновесия относительно точки А:
;
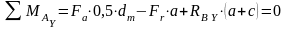отсюда
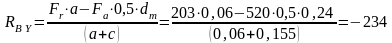Н;
Условие равновесия относительно точки В:
;
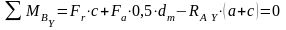отсюда
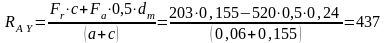Н;
Проверка:
.
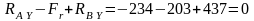в) Определяем размер изгибающих моментов в горизонтальной плоскости:
;
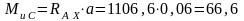Нм;
г) Определяем размер изгибающих моментов в вертикальной плоскости:
;
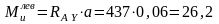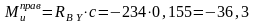Нм;
НМ;
Следовательно,
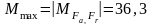Нм.
Эпюры изгибающих и крутящих моментов показаны на рисунке 5.
Суммарные реакции опор:
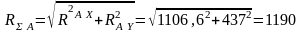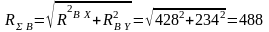Н;
Н;
Суммарный изгибающий момент под зубчатым колесом:
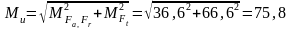Нм;
Эквивалентный момент:
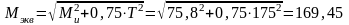Нм;
Диаметр рассчитываемого вала:
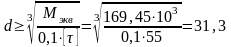мм.
Принимаем ближайшее большее стандартное значение диаметра вала равное 32 мм.