2. Общие сведения о методах расчета настроек непрерывного регулятора в одноконтурной системе

Регулятор как устройство управления в системе управления должен обеспечить необходимые свойства этой системы с учетом поведения объекта, т.е. обеспечить устойчивость системы и выполнение определенных требований по качеству управления как в установившемся, так и в динамическом режимах.

Процесс проектирования регулятора может проходить различными способами. Это могут быть эмпирические методы, основанные на измерениях, выполненных на реальном объекте. В этом случае объект должен иметь достаточно простую модель в виде апериодического звена с запаздыванием, т.е. допускать аппроксимацию вида (2.1):

, (2.1)

здесь k₀ – коэффициент усиления апериодического звена;

τ₀,с – время запаздывания;

T₀,с – постоянная времени звена.

К таким методам относятся метод колебаний Зиглера – Никольса, метод Зиглера – Никольса на основе критерия Найквиста, методы, позволяющие провести расчет настроек регулятора по известной кривой отклика.

Кроме эмпирических методов настройки регуляторов могут быть найдены на основе аналитических или графо – аналитических методов. В данном пособии рассматривается метод расширенных частотных характеристик как пример аналитического способа и метод ограничения на частотный показатель колебательности (графо-аналитический метод).

1. Метод колебаний Зиглера – Никольса

Эта процедура применима только для устойчивых объектов и выполняется следующим образом.

1. Расчет критических значений настроек регулятора

Критические значения коэффициента усиления и постоянной времени интегрирования для реально существующей системы могут быть получены опытным путем. Для этого в качестве регулятора в систему вводится пропорциональный регулятор с малым коэффициентом передачи. Затем коэффициент плавно увеличивают до тех пор, пока на выходе системы не появятся колебания. Коэффициент передачи, при котором появились колебания, определяет его критическое значение (К_кр), соответствующая частота колебаний ω_кр, по формуле определяет критическое значение времени Т_кр. На основе полученных критических значений вычисляют оптимальные настройки регуляторов различных типов (П, ПИ, ПИД) (таблица 2.1).

Критические значения могут быть рассчитаны аналитическим путем на основе критерия устойчивости Найквиста.

Для П-регулятора передаточная функция разомкнутой системы имеет вид

,

где W_р–р(s) – передаточная функция регулятора. Для П-регулятора

.

Система находится на границе устойчивости, если годограф АФЧХ разомкнутой системы проходит через точку (–1;0), т.е.

,

тогда .

Из последнего равенства определяют последовательно ; ; Т_кр.

Все вычисления выполняются по алгоритму.

2. Алгоритм:

1. Составить передаточную функцию разомкнутой системы

.

2. Подставить вместо 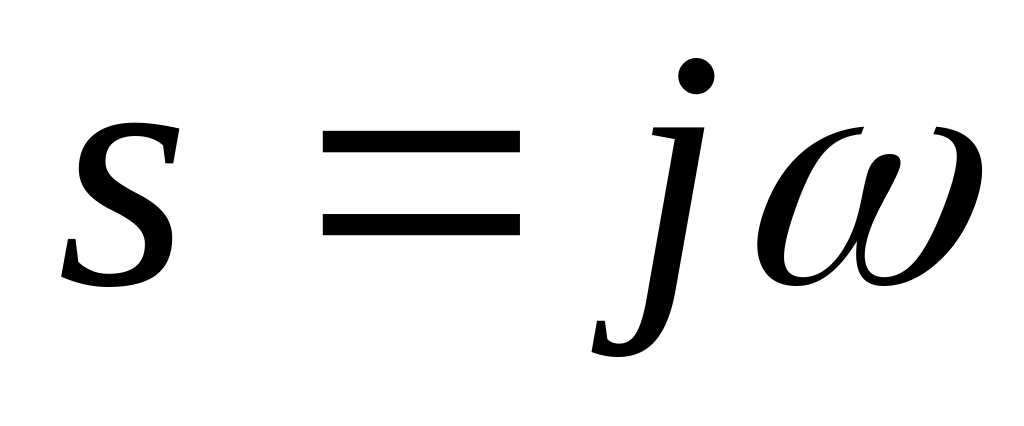, записать АФЧХ разомкнутой системы .

3. Выразить

. (2.2)

4. Записать правую часть равенства (2.2) К_кр в первой алгебраической форме и приравнять левой части:

.

5. Так как комплексные числа равны и имеют соответственно равные действительные и мнимые части, то приравнять =0 и найти .

6. Подставить в действительную часть и найти критическое значение коэффициента усиления

.

7. Найти критический период

.

8. По таблице 2.1 рассчитать настройки для заданного алгоритма управления.

9. Записать передаточную функцию разомкнутой системы (W_p(s)) с выбранным регулятором

.

10. Записать передаточную функцию замкнутой системы (W_зам(s)), если обратная связь единичная, то W_зам(s) будет определена как:

.

11. Записать изображение переходной характеристики (H(s)).

.

12. Найти оригинал переходной характеристики (h(t))

.

13. Построить переходную характеристику (h(t)).

14. Определить прямые показатели качества (время регулирования (t_р) при заданной точности измерения Δ; в технических системах достаточно часто она принимается равной пяти процентам от установившегося значения ; перерегулирование ,

где h_уст – установившееся значение выходной величины при единичном воздействии;

h_max – максимальное значение выходной величины.

15. Если полученные показатели качества получились хуже заданных, то настройки регулятора несколько изменяют (k_р уменьшают, T_и увеличивают), добиваясь требуемых показателей качества. Одной из причин такого несоответствия может быть отличие математического описания объекта от апериодического типа, на основе которого строились таблицы Зиглера-Никольса.

Таблица 2.1. – Оптимальные настройки регуляторов по методу Зиглера-Никольса

2.1.3. Пример 2.1. Найти настройки ПИ и ПИД-регуляторов, оценить прямые показатели качества. Передаточная функция объекта имеет вид:

.

Решение:

;

;

;

;

;

;

;

.

Для ПИ-регулятора с передаточной функцией

;

;

;

;

.

Для настроек, вычисленных по таблице Зиглера-Никольса, получили перерегулирование σ=30,2%, t_p=49,9 (рисунок 2.1).

Рисунок 2.1. – Переходная характеристика системы с ПИ-регулятором

Для ПИД-регулятора с передаточной функцией ,

;

;

;

.

Для вычисления было выбрано в этом примере значение .

;

.

Показатели качества системы с настройками из таблицы Зиглера-Никольса σ=47%, t_p=46,7; ( рисунок 2.2).

Рисунок 2.2. – Переходная характеристика системы с ПИД-регулятором