1.11. Линейный интегральный критерий

Изображение переходной характеристики связано с передаточной функцией соотношением

(1.10)

В преобразовании Лапласа справедливо следующее предельное соотношение

(1.11)

Тогда линейный интегральный критерий может быть вычислен по формуле

(1.12)

1.12. Вычисление линейного интегрального критерия для некоторых типов регуляторов

1.12.1. Системы с И – регулятором

Пример 1.5. Для структурной схемы с произвольным возмущением ƒ(t) (рисунок 1.17) вычислить значение линейного интегрального критерия.

W_ƒ(s)

F(s)

U (s) X(s)

Рисунок 1.17. – Структурная схема одноконтурной системы с регулятором

Решение. Передаточная функция относительно возмущения F(s) имеет вид (W_зƒ(s)):

Тогда

Здесь P_m1(s); P_m2(s); Q_n1(s); Q_n2(s) – многочлены, записанные в стандартной форме; m1 ≤ n1; m2 ≤ n2.

После упрощения полученных выражений и перехода к пределу при s=0 линейный интегральный критерий принимает значение

(1.13)

Для уменьшения значения линейного интегрального критерия нужно в допустимых пределах увеличивать коэффициент передачи И – регулятора.

1.12.2. Системы с ПИ и ПИД – регуляторами

Изображение переходной характеристики в принятых (в п. 1.12.1.) обозначениях записывается как

о .переходной характеристики встики в принятых пределу при ымулеие00000000000000000000000000000000000000000000000000000000000

После приведения к общему знаменателю в знаменателе этого выражения, деления и перехода к пределу линейный интегральный критерий может быть вычислен по формуле:

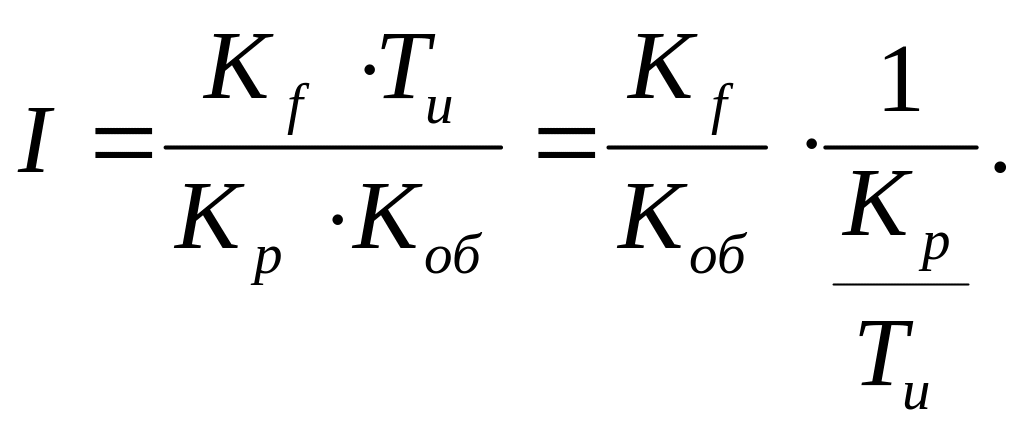(1.14)

Эта же формула получается и для ПИД – регулятора, поэтому для минимизации линейного интегрального критерия отношение коэффициента передачи регулятора и его постоянной времени интегрирования должно быть как можно большим, если в системе управления используются ПИ и ПИД – регуляторы.

1.12.3. Системы с пропорциональным регулятором

По правилу предельных переходов

.

Для систем управления с пропорциональным регулятором уставившееся значение переходной характеристики

, (1.15)

поэтому для минимизации остаточной неравномерности в системах с пропорциональным регулятором следует стремиться к возможно большему значению его коэффициента передачи.

1.12.4. Расчет среднеквадратической ошибки регулируемой величины

Среднеквадратическая ошибка регулируемой величины σ_x, вызванная возмущающим воздействием, может быть вычислена, если задана спектральная плотность возмущающего воздействия S_ƒƒ(ω).

Дисперсия регулируемой непрерывной величины (σ_x) выражается через ее спектральную плотность (S_xx)

(1.16)

Спектральная плотность регулируемой величины связана со спектральной плотностью возмущающего воздействия соотношением

, (1.17)

где Ф_xƒ(jω) – амплитудно-фазовая частотная характеристика замкнутой системы по возмущению.

Для дискретной системы интеграл рассчитывается по формуле

(1.18)

Замечание: фактические пределы интегрирования могут быть значительно меньше и определяются физической природой случайного возмущающего воздействия.