Критерии устойчивости
Устойчивость линейной системы можно определить, не вычисляя корней характеристического уравнения, с помощью критериев устойчивости.
С развитием вычислительной техники проблемы определения корней характеристического уравнения нет, однако критерии устойчивости могут ответить на другие вопросы, такие как: каков запас устойчивости, что нужно сделать, чтобы неустойчивая система стала устойчивой и т.д.
Критерии устойчивости делятся на алгебраические и частотные. Алгебраические критерии исследуют коэффициенты характеристического уравнения, частотные строятся на основе либо характеристического уравнения, либо передаточной функции.
Наиболее известным алгебраическим критерием является критерий Гурвица (1895г). Из коэффициентов характеристического уравнения
строится главный определитель Гурвица ∆n:
Если все определители, построенные от верхнего левого угла:
;
;
…
– положительны, то система устойчива, если среди них есть отрицательные, то неустойчива.
Критерий позволяет определить значения параметров системы, обеспечивающие ее устойчивость. Для этого ∆n–1 приравнивают нулю (система находится на границе устойчивости) и разрешают получившееся уравнение относительно интересующего параметра.
Замечание.
Так как
,
а по необходимому условию устойчивости
все коэффициенты характеристического
уравнения положительны, то знак ∆n
определяется знаком ∆n-1.
Частотные критерии основываются на принципе изменения аргумента комплексной функции, получаемой заменой оператора s на мнимую переменную jω.
В критерии Михайлова (1938г) функция строится на основе характеристического полинома А(s) (знаменателя передаточной функции ), в ней выделяют действительную и мнимую часть:
.
Пример 1.3. Передаточная функция системы имеет вид W(s):
;
Собственный
оператор
,
функция Михайлова
;
;
.
Для того, чтобы система была устойчива, необходимо и достаточно, чтобы график функции Михайлова (годограф Михайлова) начинался на действительной положительной полуоси и последовательно проходил против часовой стрелки столько четвертей, какова степень характеристического уравнения.
Пример 1.4. Характеристический многочлен имеет вид
.
Годограф Михайлова имеет вид, приведенный на рисунке 1.12. Сделать вывод об устойчивости системы.
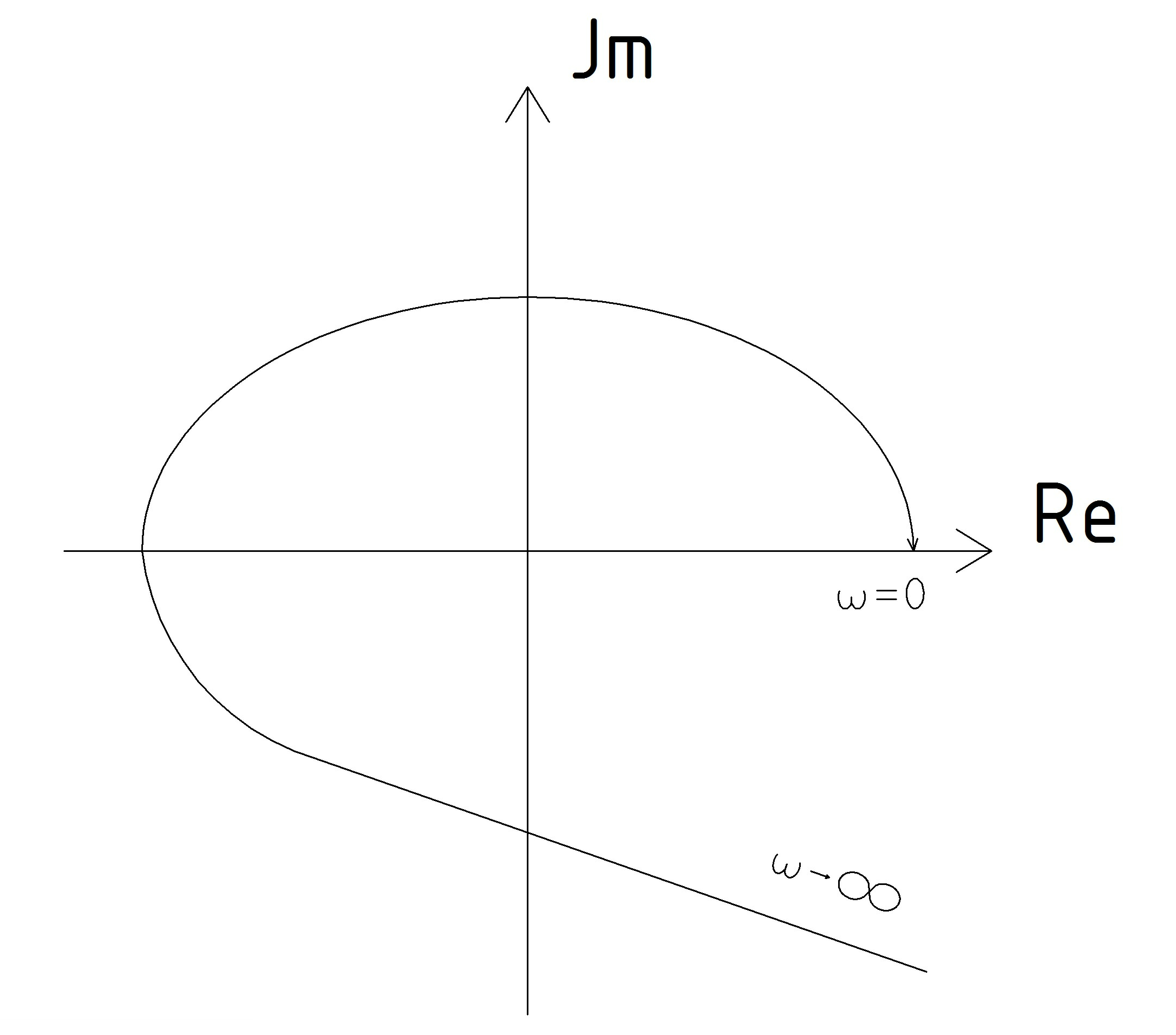
Рисунок 1.12. – Годограф Михайлова к примеру 1.4
Решение. Система устойчива, т.к. при ω=0 годограф начинается на действительной положительной полуоси, при увеличении частоты ω график движется против часовой стрелки, последовательно проходит четыре квадранта, что равно степени характеристического полинома.
Критерий Михайлова может применяться при определении диапазона изменения одного или двух параметров системы (метод D-разбиения), обеспечивающих устойчивость системы.
Названные выше критерии были разработаны для безинерционных систем, для систем с запаздыванием эти критерии либо оказываются неприменимыми, либо требуются дополнительные исследования.
Более универсальным критерием является критерий Найквиста. Он позволяет определить устойчивость замкнутой системы по амплитудно-фазо-частотной характеристике (АФЧХ) разомкнутой системы.
Если разомкнутая система была устойчива и в ней нет интегрирующих звеньев, то система в замкнутом состоянии останется устойчивой, если АФЧХ разомкнутой системы не охватывает точку (–1; j0).
Если
в устойчивой разомкнутой системе есть
γ интегрирующих звеньев, то система в
замкнутом состоянии останется устойчивой,
если АФЧХ разомкнутой системы после
дополнения дугой бесконечно большого
радиуса на угол
против часовой стрелки не охватывает
точку (–1; j0).
Если разомкнутая система была неустойчива (число правых корней L)
то при замыкании система может стать устойчивой, если АФЧХ разомкнутой системы имеет разность между числом положительных и отрицательных переходов действительной полуоси на интервале (-∞;-1) при изменении частоты от 0 до ∞, равную L/2.
Замечание. Переход считается положительным, если совершается сверху вниз, отрицательным, если снизу вверх (рисунок 1.13).
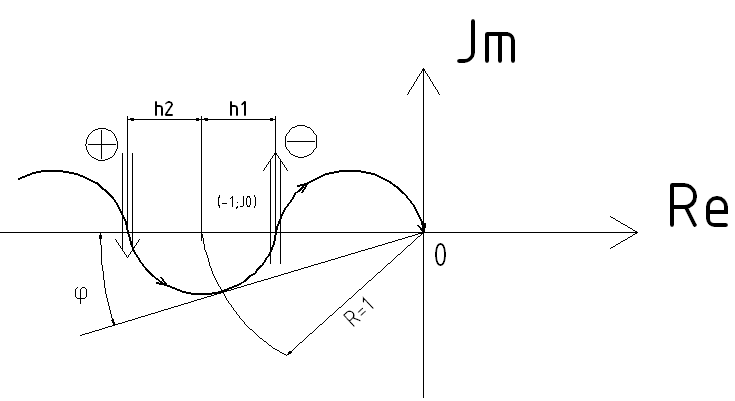
Рисунок 1.13. – Иллюстрация положительности и отрицательности переходов
Замечание. Если характеристика W(jω) начинается на отрезке (–∞;–1) при ω=0 и заканчивается на нем при ω→∞,то в этих случаях считают, что она совершает изменение на полпериода.
Критерий Найквиста позволяет найти запас устойчивости по амплитуде (h1; h2) и по фазе (φ), данный критерий используется при создании различных алгоритмов расчета оптимальных настроек регуляторов.