1.4. Построение передаточной функции одноконтурной системы

Систему называют одноконтурной, если после размыкания главной обратной связи в ней не остается других обратных связей (локальных) (рисунок 1.8).

Рисунок 1.8. – Пример одноконтурной системы

Последовательно применив правила 1-3, можно получить передаточную функцию такой системы (рисунок 1.9, 1.10).

Согласно правила 2 элементы 2 и 3 можно заменить эквивалентным (2-3) с передаточной функцией (рисунок 1.9).

Рисунок 1.9. – Структурная схема с эквивалентным звеном 2-3

Элементы 1, 2-3, 4 соединены последовательно, поэтому по правилу 1 их тоже можно заменить эквивалентным элементом 1-4 с передаточной функцией (рисунок 1.10).

Рисунок 1.10. – Структурная схема после преобразования участка с последовательным соединением звеньев

Используя правило 3, с учетом того, что, при отсутствии каких-либо дополнительных указаний на сумматоре, обратная связь считается отрицательной, записываем передаточную функцию исходной системы W(s), приведенной на рисунке 1.8:

.

1.5. Построение передаточных функций многоконтурных систем

Система называется многоконтурной, если после размыкания какой-либо обратной связи, в ней остаются другие обратные связи.

Обратная связь, которая охватывает только часть звеньев, называется локальной или местной обратной связью.

Обратная связь, которая охватывает все элементы прямой цепи, называют глобальной обратной связью.

Если коэффициент передачи обратной связи равен единице, то её называют единичной.

В многоконтурных системах сначала избавляются от локальных обратных связей, заменяя участки структурной схемы с местными обратными связями эквивалентными элементами с более сложными передаточными функциями так, чтобы исходная система приняла вид эквивалентной одноконтурной системы, к которой применяют правила, изложенные в п.1.4.

Пример 1.1. Построить передаточную функцию системы, приведенной на рисунке 1.11.

U

(s) X(s)

Рисунок 1.11. – Структурная схема двухконтурной системы

Решение. Элемент с передаточной функцией охвачен локальной обратной связью с передаточной функцией , поэтому этот участок может быть заменен эквивалентным элементом с передаточной функцией . Элементы с передаточными функциями ; ; соединены последовательно, поэтому их последовательное соединение заменим элементом с передаточной функцией, представляющей собой произведение их передаточных функций . Тогда элемент охвачен обратной связью с передаточной функцией , поэтому передаточная функция двухконтурной системы, приведенной на рисунке 1.11, может быть задана как

.

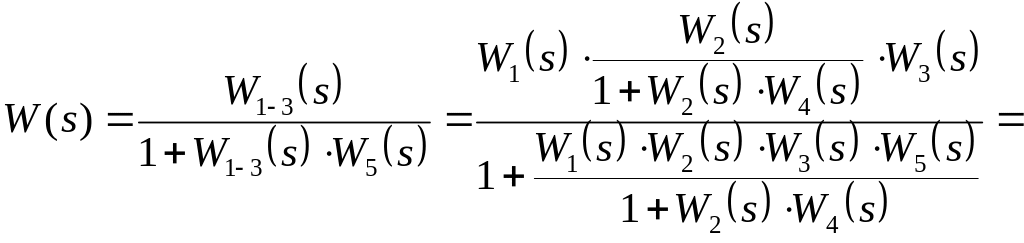
1.6. Устойчивость линейных непрерывных систем

Свойство устойчивости систем является одним из наиболее важных для её работоспособности, линейная система автоматического управления считается устойчивой, если после окончания воздействия по истечении некоторого времени она возвращается в исходное состояние (с точностью до проведенных измерений).

Если после окончания воздействия система неограниченно отдаляется от исходного состоянии, то её называют неустойчивой.

Если после окончания воздействия система приходит в другое состояние, отличное от исходного, то её называют безразлично устойчивой.

Устойчивость системы можно определить, исследуя её математическое описание (дифференциальное уравнение, операторное уравнение, передаточную функцию, частотные или временные характеристики).

Математическое описание поведения системы получают на основе физических закономерностей процессов, используя различные приемы, такие как декомпозиция, линеаризация и упрощение. Такие дифференциальные уравнения называют дифференциальными уравнениями первого приближения. Очень часто они имеют вид линейных неоднородных дифференциальных уравнений с постоянными коэффициентами, решение которых определяется в виде суммы двух слагаемых: свободной составляющей и вынужденной, вызванной внешними воздействиями . Свободная составляющая определяется только свойствами системы. Это решение линейного однородного дифференциального уравнения (ЛОДУ), которое находится на основе характеристического уравнения (характеристическое уравнение можно получить, приравняв к нулю, собственный оператор системы, т.е. знаменатель передаточной функции).

В соответствии с определением устойчивости по А.М. Ляпунову система будет асимптотически устойчива, если с течением времени при свободная составляющая будет стремиться к нулю, т.е. или .

Решение ЛОДУ определяется как линейная комбинация решений вида ; ; ; , или в общем случае и , где – корни характеристического уравнения, . Для того, чтобы , действительная часть корней характеристического уравнения должна быть отрицательной.

Таким образом, условие устойчивости линейной системы может быть сформулировано следующим образом: для того, чтобы линейная система была асимптотически устойчива, необходимо и достаточно, чтобы все корни её характеристического уравнения имели отрицательные действительные части, т.е. были левыми.

Пример 1.2. Система имеет передаточную функцию

.

Определить, устойчива ли она.

Решение. Характеристическое уравнение для такой системы имеет вид . Корни характеристического уравнения s₁ = –1;

s₂ = –10, s₃ = –5 имеют отрицательные действительные части, следовательно, система устойчива.