1.2. Элементарные звенья

Часть системы, имеющая своим описанием дифференциальное уравнение не выше второго порядка, называется элементарным звеном. К основным элементарным звеньям относятся пропорциональное (усилительное) звено, дифференциальное, интегрирующее, апериодическое (инерционное), колебательное, форсирующее первого порядка, форсирующее второго порядка. Перечисленные элементарные звенья имеют отрицательные вещественные части корней характеристического уравнения, поэтому являются устойчивыми звеньями, их еще называют минимально-фазовыми. Передаточные функции элементарных звеньев и их дифференциальные уравнения приведены в таблице 1.1, обозначения соответствуют использованным выше, т.е. x(t) – реакция, выходная характеристика, u(t) – входное воздействие.

Таблица 1.1. – Элементарные звенья

№	Название	Передаточная функция	Дифференциальное уравнение	Примечание
1	Пропорциональное
2	Дифференци-рующее (идеальное)			Tд – постоянная дифференцирования
3	Интегрирующее			Tu – постоянная интегрирования
4	Апериодическое (инерционное)			T – постоянная времени, k – коэффициент усиления

Продолжение таблицы 1.1

5	Колебательное		или	T – постоянная времени, k – коэффициент усилении, ξ – постоянная демпфирования
6	Форсирующее первого порядка
7	Форсирующее второго порядка

2. Правила преобразования структурных схем

Для изучения систем автоматического управления широко используются структурные схемы, соответствующие полученному математическому описанию. Элемент такой схемы обозначает то или иное элементарное звено. Операция суммирования производится элементом, называемым сумматором. Под суммированием понимается как сложение, так и вычитание сигналов.

Элементы структурных схем могут соединяться тремя принципиально разными способами.

При последовательном соединении выходной сигнал предыдущего элемента x₁(t) (реакция на входной сигнал u(t)) передается полностью на вход последующего элемента (рисунок 1.1) с выходной характеристикой x(t).

Рисунок 1.1. – Последовательное соединение элементов 1 и 2

Введя изображение сигналов и используя понятие передаточной функции элементов 1 и 2, получаем:

Тогда передаточная функция системы элементов 1 и 2 записывается как

Правило 1. При последовательном соединении элементов их передаточные функции перемножаются.

При параллельно – согласном включении элементов 1 и 2 входной сигнал u(t) подается на вход обоих элементов, реакции x₁(t) и x₂(t) потом складываются на сумматоре 3 (рисунок 1.2), определяя таким образом выходную характеристику x(t).

Рисунок 1.2. – Параллельно – согласное соединение элементов 1 и 2

После перехода к изображениям

получаем

Тогда передаточная функция W(s) системы, приведенной на рисунке 1.2, имеет вид

Правило 2. При параллельно – согласном соединении элементов их передаточные функции складываются.

Параллельно – встречным соединением или соединением с обратной связью называется такое соединение, когда сигнал с выхода первого элемента x(t) подается полностью или после преобразования вторым элементом (u₂(t)) обратно на вход первого элемента со знаком плюс или минус, изменяя тем самым входное воздействие u(t) (рисунок 1.3).

Рисунок 1.3. – Параллельно – встречное соединение

Операторные уравнения в изображении по Лапласу, описывающие движение сигналов, имеют вид:

,

.

Знак плюс соответствует положительной обратной связи, минус – отрицательной. После простых алгебраических преобразований получаем передаточную функцию W(s) системы, приведенной на рисунке 1.3:

,

где знак плюс соответствует отрицательной обратной связи, знак минус – положительной.

В сложных схемах с перекрещивающимися обратными связями кроме перечисленных трех простейших правил структурных преобразований используют перенесение сумматоров и узлов.

При переносе сумматора по ходу сигнала (рисунок 1.4) необходимо добавить звено с передаточной функцией звена, через которое переносится сумматор, а если против хода сигнала, то необходимо добавить звено с передаточной функцией, обратной передаточной функции звена, через которое переносится сумматор (рисунок 1.5).

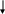ƒ

а

) U₀ U₁ X₁ X

ƒ

б ) U₀ U₁ U₂ X

Рисунок 1.4. – Перенос сумматора по ходу сигнала: а) – исходная схема; б) – после переноса сумматора

ƒ

а) U₀ U₁ U₂ X

ƒ

б ) U U₂ X

Рисунок 1.5. – Перенос сумматора против хода сигнала: а) – исходная схема; б) – после переноса сумматора

При переносе узлов также необходимо добавлять звенья.

Если узел переносится по ходу сигнала, то добавляется звено с передаточной функцией, обратной передаточной функции звена, через которое переносится узел (рисунок 1.6).

а)

U X

X₁

б)

U X

X₁

Рисунок 1.6. – Перенос узла по ходу сигнала: а) – исходная схема; б) – после переноса узла

Если узел переносится против хода сигнала, то добавляется звено с передаточной функцией, равной передаточной функции звена, через которое переносится узел (рисунок 1.7).

а) U X

X₁

б

) U X

X₁

Рисунок 1.7. – Перенос узла против хода сигнала: а) – исходная схема; б) – после переноса узла

Эти правила относятся к правилам структурных преобразований, которые позволяют записать передаточную функцию сложной системы, если известны передаточные функции элементов, образующих эту систему.