3.4. Особенности расчета настроек регуляторов в двухконтурной системе с неединичными обратными связями
В пункте 3.3. рассматривались системы с единичными обратными связями. В общем случае они могут быть неединичными (Рисунок 3.6).
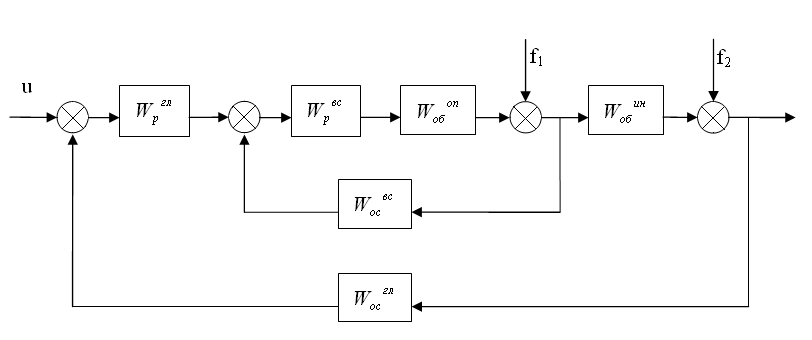
Рисунок 3.6. – Структурная схема двухконтурной системы управления с неединичными обратными связями
При первоначальном расчете настроек главного регулятора эквивалентная передаточная функция участка с местной обратной связью имеет вид
.
С
учетом предположения, что
,
в расчётах данная передаточная функция
заменяется эквивалентной передаточной
функцией:
.
Для применения многих методик расчёта настроек регулятора необходимо структурную схему привести к виду, где передаточная функция цепи обратной связи равна единице (рисунок 3.7).
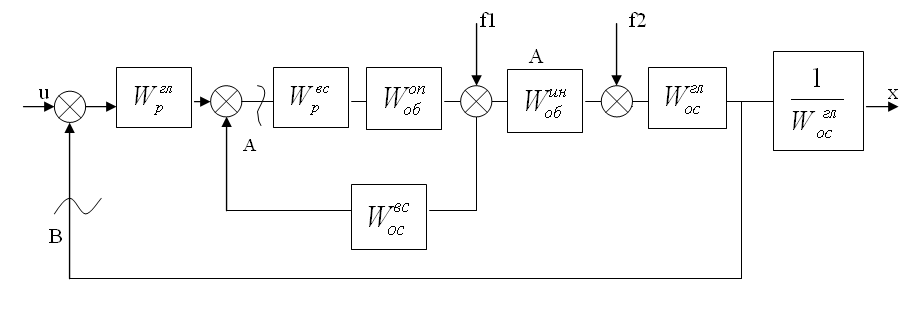
Рисунок 3.7. – Структурная схема, приведённая к виду с единичной обратной связью
Тогда
на первом этапе для расчёта настроек
главного регулятора схему размыкают в
точке B.
Передаточная функция разомкнутой цепи
при условии, что
имеет
вид:
Структурная схема для расчёта настроек вспомогательного регулятора
после размыкания в точке А приведена на рисунке 3.8.
Рисунок 3.8. – Структурная схема для расчета настроек вспомогательного регулятора с учетом неединичных обратных связей
Передаточная функция для расчета настроек вспомогательного регулятора (рисунок 3.8) имеет вид:
В
передаточной функции главного регулятора
используются
оптимальные настройки, найденные тем
или иным методом по передаточной функции
при
условии, что
.
При уточнении настроек главного регулятора передаточная функция разомкнутой системы строится по структурной схеме, приведенной на рисунке 3.7, после размыкания в точке B и имеет вид:
4. Расчет настроек дискретных регуляторов
4.1. Основные определения
В системах автоматического управления рабочая информация представляется в виде сигналов, которые по отношению ко времени могут быть непрерывными и дискретными.
Процесс
преобразования непрерывного сигнала
в дискретный называется квантованием
или дискретизацией. Квантование может
выполняться по уровню, т.е. по достижению
сигналом некоторого уровня
,
что происходит в произвольные моменты
времени (рисунок 4.1). Системы с таким
способом дискретизации называют
релейными.
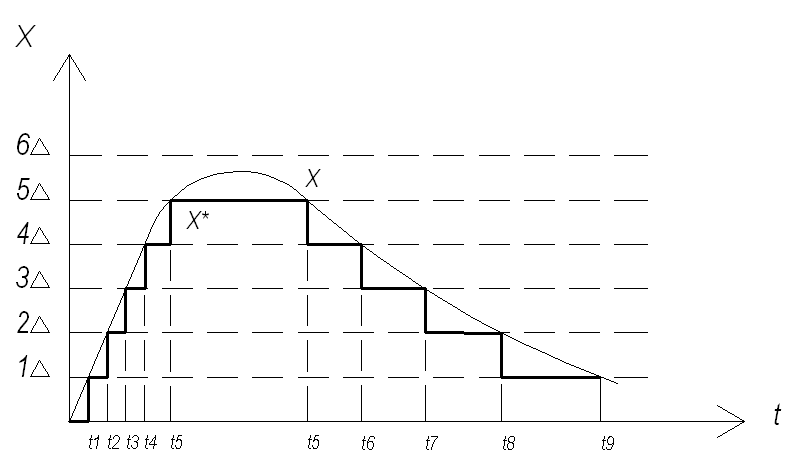
Рисунок 4.1. – Квантование по уровню
В импульсных системах производится квантование по времени, т.е. в определенные, в большинстве случаев равноотстоящие, моменты времени выделяются значения непрерывного сигнала (рисунок 4.2).
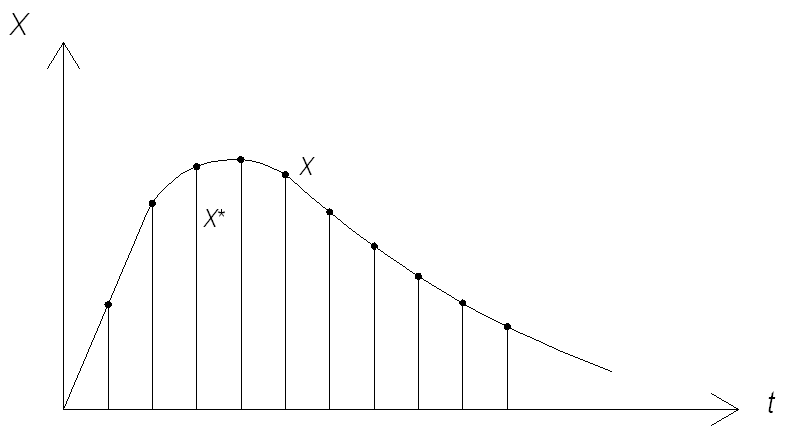
Рисунок 4.2. – Квантование по времени
Если моменты времени отстают друг от друга на некоторую постоянную величину, то её называют периодом квантования или периодом дискретизации (Т).
Квантование может выполняться одновременно и по времени, и по уровню. Значения непрерывного сигнала через определенные моменты времени заменяются фиксированными по уровню дискретными значениями, ближайшими к значениям X в дискретные моменты времени (рисунок 4.3).
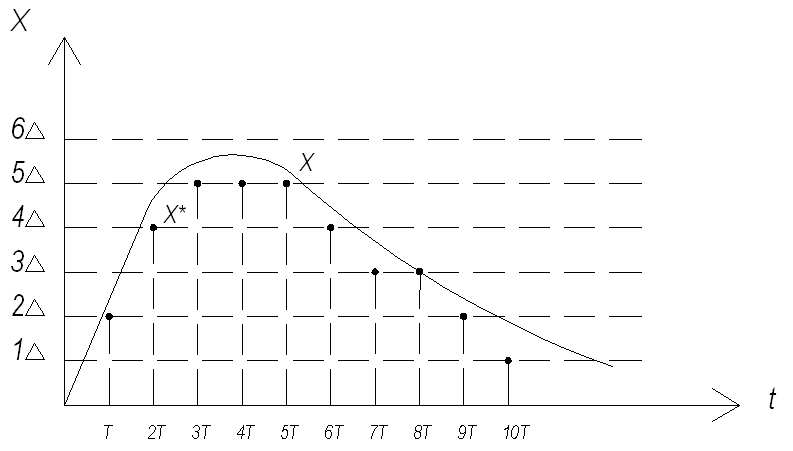
Рисунок 4.3 – Квантование по уровню и по времени
Такие системы называются релейно-импульсными.
Замечание. Цифровые системы управления относятся к релейно-импульсному классу систем.
Среди большого разнообразия дискретных систем выделяют две основные категории.
К первой категории относят системы дискретные по своей физической природе, т.к. информация в них существует только в дискретные моменты времени, динамика процессов в таких системах может быть представлена только дискретными моделями, например радиолокационные системы обнаружения и сопровождения цели, системы планирования и управления в социальной сфере и т.д.
Ко второй категории относятся системы, в которых информационные потоки имеют непрерывный характер, но для получения новых свойств их намеренно приводят к дискретной форме, что позволяет повысить надежность и точность систем, уменьшить габариты, стоимость, использовать в системах управления новейшие достижения прогресса.
В процессе приведения непрерывного сигнала к дискретной форме в импульсных системах происходит преобразование информации в определенные моменты времени в последовательность импульсов, параметры которых (амплитуда, длительность, фаза, частота) зависят от значений этого сигнала.
Если значение непрерывного сигнала определяет амплитуду импульса, то такой способ преобразования называют амплитудно-импульсной модуляцией (АИМ).
Амплитуда импульса может оставаться неизменной, а длительность импульса в течение периода квантования определяется амплитудой непрерывного сигнала в момент квантования. Такое преобразование называют широтно-импульсной модуляцией (ШИМ).
Если же в процессе модуляции меняется фаза импульса, то такое преобразование называют фазоимпульсной модуляцией (ФИМ).
При постоянной амплитуде, длительности и фазе импульса в процессе преобразования может изменяться частота импульсов, такую модуляцию называют частотно-импульсной (ЧИМ), к данному виду модуляции относят и числоимпульсную модуляцию, при которой в зависимости от амплитуды непрерывного сигнала изменяется число импульсов на периоде квантования.
Импульсная модуляция может быть первого и второго рода.
Если считанное в процессе квантования значение непрерывного сигнала в течение периода квантования не изменяется (хотя сам непрерывный сигнал изменяется) и определяет процесс модуляции, то импульсную модуляцию относят к первому роду.
Возможен вариант, когда в процессе модуляции в течение периода квантования учитывается изменение непрерывного сигнала, тогда модуляция относится ко второму роду.
В зависимости от вида модуляции импульсные системы принято подразделять на следующие виды: амплитудно-импульсные системы (АИС), широтно-импульсные (ШИС), фазоимпульсные (ФИС), частотно-импульсные (ЧИС) и др.
Большая часть типов импульсных систем относится к нелинейным системам.
Амплитудно-импульсные системы могут быть как линейными системами, так и нелинейными.
В зависимости от свойств импульсной системы применяется тот или иной математический аппарат для построения математического описания при решении задач анализа и синтеза систем такого рода.
4.2. Структурные схемы импульсных систем
В общем случае любая одноконтурная импульсная автоматическая система (ИАС) может быть представлена в виде двух частей, взаимодействующих друг с другом: импульсной (ИЧ) и непрерывной (НЧ) (рисунок 4.4). Непрерывную часть образуют объект управления, исполнительное устройство, усилитель мощности, датчики.
E
U
X
t
t
t
g E U
x
ИЧ
НЧ
Рисунок 4.4. – Обобщенная структурная схема замкнутой импульсной системы
Импульсная часть, как правило, является управляющим устройством, состоит из импульсного устройства и функциональных элементов, выполняющих импульсное преобразование сигнала. Она может быть реализована в виде импульсных регуляторов, ключей, цифровых вычислительных устройств с аналогово-цифровыми (АЦП) и цифро-аналоговыми преобразователями (ЦАП) и т.д.
Функционально импульсная часть представляет собой некоторый преобразователь непрерывного сигнала в импульсное управляющее воздействие того или иного вида, зависящее от непрерывного сигнала ошибки в равноотстоящие моменты квантования.
Каков бы ни был состав импульсной части, в ней всегда есть реальный импульсный элемент (РИЭ), преобразующий непрерывный сигнал ошибки в последовательность импульсов (рисунок 4.5).
E(t)
U(t)
t t
g
E U
X
РИЭ
НЧ
Рисунок 4.5. – Структурная схема импульсной системы с реальным импульсным элементом
При исследовании импульсных систем РИЭ заменяют последовательным соединением идеального импульсного элемента (ИИЭ) и формирующего элемента (ФЭ) (рисунок 4.6).
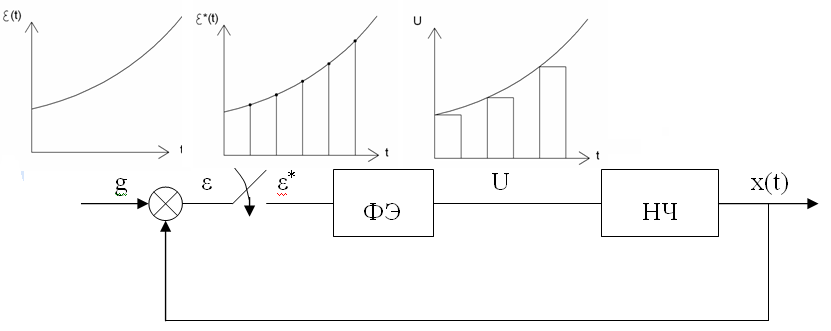
Рисунок 4.6. – Структурная схема импульсных систем с идеальным импульсным элементом
На
вход идеального импульсного элемента
подается непрерывный сигнал ε(t),
на выходе его формируются идеальные
мгновенные импульсы в виде
функций,
соответствующие значениям входного
сигнала в моменты квантования. Формирующий
элемент преобразует эти импульсы в
импульсы, соответствующие выходной
импульсной последовательности реального
импульсного элемента. Эта реакция
формирующего элемента на
импульсы
при площади мгновенного импульса, равной
единице, является импульсной переходной
или весовой характеристикой формирующего
элемента(
).
Весовую характеристику в виде единичного импульса прямоугольной формы длительности γТ на интервале Т (рисунок 4.7) можно изобразить разностью двух единичных функций:
или
при
.
1(t)
1
0
T
-1
Рисунок 4.7. – Изображение единичного импульса разностью двух единичных функций
Изображение
;
изображение функции
подчиняется теореме о запаздывании и
равно
,
таким образом изображение единичного
импульса имеет вид
.
Так
как изображение весовой функции звена
есть его передаточная функция, то
передаточная функция звена, формирующего
единичные импульсы, равна
.
Отношение
длительности импульса к периоду
квантования называют скважностью
.
Если амплитуда импульса не изменяется в течение периода квантования, такое устройство называют фиксатором (экстраполятором, формирователем) нулевого порядка.
Имеются формирующие устройства с другими типовыми формами импульсов, для некоторых из них передаточные функции приведены в таблице 4.1.
Таблица 4.1. – Передаточные функции некоторых формирующих устройств для типовых форм импульсов
|
Форма импульса |
Передаточная функция |
Передаточная функция при γ «1 |
1. |
|
|
|
2. |
|
|
|
Продолжение таблицы 4.1
3. |
|
|
|
Для удобства анализа объединяют непрерывную часть импульсной системы и формирующее устройство. Это последовательное соединение непрерывной части и формирующего устройства называют приведенной непрерывной частью, тогда импульсные системы с амплитудной модуляцией первого рода независимо от формы реальных импульсов представляют в виде соединения идеального импульсного элемента и приведенной непрерывной части (рисунок 4.8).
Wфэ
Wнч(s)
g
E
T
пнч
Х
Рисунок 4.8. – Эквивалентная структурная схема импульсной системы с амплитудно-импульсной модуляцией
Коэффициент усиления формирующего устройства относят к непрерывной части.
Передаточная функция приведенной непрерывной части равна
.
Цифровые системы управления можно исследовать, приняв за основу эквивалентную структурную схему (рисунок 4.8). Так как при использовании аналогово-цифровых и цифро-аналоговых преобразователей, имеющих достаточно большое число разрядов, эффекты квантования по уровню могут не учитываться, импульсная часть в этом случае представляется в виде линейного дискретного фильтра, а формирующее устройство является экстраполятором (фиксатором) нулевого порядка.
4.3. Структурные схемы импульсных систем с дискретными регуляторами
Системы автоматического управления, в которых устройство управления работает в дискретном режиме, а объект управления в непрерывном режиме, относятся к системам смешанного типа по отношению ко времени. В них может быть выделена дискретная часть и приведенная непрерывная часть. В приведенную непрерывную часть относят непрерывный объект и формирующее устройство определенного типа, а дискретная часть состоит из идеального импульсного элемента и дискретного регулятора.
В зависимости от типа управляющего сигнала по отношению ко времени (дискретный или непрерывный) структурная схема для расчета может принимать разный вид.
Если
задающее воздействие
является непрерывным, то расчетная
структурная схема в общем случае имеет
вид (рисунок 4.9).
Передаточная
функция прямой цепи
в
дискретной форме имеет вид:
,
где
-
передаточная функция дискретной части;
-
z-передаточная
функция приведенной непрерывной части.
Замечание. Z-преобразование не обладает распределительным свойством, т.е.
Z-передаточная
функция замкнутой системы
вычисляется
по формуле:
Если
задающее воздействие
имеет
дискретную форму, то расчетная структурная
схема в общем случае имеет вид (рисунок
4.10).
В
этом случае z-передаточная
функция прямой цепи
рассчитывается так же, как и в первом
случае:
z-передаточная функция для замкнутой системы будет иметь вид:
.
4.4. Построение z-передаточной функции приведенной непрерывной части
4.4.1. Формирующий элемент – фиксатор нулевого порядка
Передаточная функция приведенной непрерывной части, состоящей из фиксатора нулевого порядка и объекта, имеет вид:
Z-передаточная
функция приведенной непрерывной части
определяется по формуле:
На основе теоремы о запаздывании
z-передаточная функция приведенной непрерывной части рассчитывается по формуле:
4.4.2. Формирующие элементы других типов
Для формирующих элементов других типов z-передаточную функцию нужно рассчитывать по общей формуле
4.4.3. Переход от передаточных функций непрерывной системы к z-передаточным функциям разложением на простые дроби
Z-передаточные функции приведенной непрерывной части могут быть найдены разложением её передаточной функции на простые дроби методом неопределенных коэффициентов. После нахождения неопределенных коэффициентов переходят к оригиналам, соответствующим каждой дроби, а затем подбирается z-изображение для каждого оригинала по таблице.
Если
в системе используется фиксатор нулевого
порядка, то для нахождения z-передаточной
функции от
нужно выполнить следующие шаги.
Разложить
на простые дроби:
Привести
правую часть (4.1) к общему знаменателю,
раскрыть скобки, сгруппировать слагаемые
с одинаковыми степенями и, получив
систему уравнений относительно
,
разрешить систему относительно этих
коэффициентов
.
Подставить их в правую часть (4.1) и найти оригинал для каждой дроби.
Для
оригинала каждой дроби найти z-изображение,
затем привести выражение к общему
знаменателю и домножить на
.
В пакете Mathcad переход от изображения по Лапласу к z-изображению выполняется по схеме:
W(s)
invlaplace, s
(оригинал);
(оригинал) ztrans, t W(z), при этом период дискретизации по умолчанию принимается равным единице. Чтобы учесть период дискретизации, нужно от оригинала перейти к z-изображению, используя таблицу (Приложение А).
В пакете Matlab переход к z-изображению выполняется командой “c2d” (continuous to discrete). Общий вид команды: Wz=c2d(W,T), где W – передаточная функция заданного объекта в непрерывной форме, T- период дискретизации, по умолчанию программа выбирает фиксатор нулевого порядка.
4.4.4. Учет запаздывания в непрерывной части
Если
в непрерывную часть входит звено с
чистым запаздыванием, что в передаточной
функции соответствует наличию множителя
,
то в z-передаточной
функции появляется множитель
,
где
(
-период
дискретизации).
Если
не является целым числом, то может
использоваться модифицированное или
смещенное z-преобразование,
тогда
,
где
,
-
целое число, передаточная функция в
этом случае
.
Обычно такая передаточная функция не используется, так как практически всегда для оценки качества работы дискретной системы достаточно знания передаточных функций, полученных на основе обычного z-преобразования.
4.4.5. Пример расчета z-передаточной функции приведенной непрерывной части
Приведенная непрерывная часть системы представляет собой последовательное включение фиксатора нулевого порядка и объекта с заданной передаточной функцией
Найти z-передаточную функцию.
Решение:
Z-передаточная
функция в этом случае (
)
рассчитывается по формуле
.
Выберем
период дискретизации
,
как наибольший общий делитель постоянных
времени
,
,
,
тогда
Для
вычисления Z-изображения
для
раскладываем его на простые дроби:
Решаем систему уравнений, находим коэффициенты:
Подставляем найденные коэффициенты в полученное выражение:
Т.к.
,
,где
;
множителю,
соответствующему запаздыванию в
непрерывной системе (
),
в Z-преобразовании
соответствует множитель
,
(
),
тогда
,
Z-передаточная функция приведенной непрерывной части с учетом фиксатора нулевого порядка
В пакете «Matlab» для получения z-передаточной функции можно задать передаточную функцию объекта в непрерывной форме, затем воспользоваться командой c2d.
Последовательность команд будет выглядеть следующим образом:
задание передаточной функции объекта
sys1=tf([0.7],[2400 100 1],’inputdelay’,40)
В квадратных скобках необходимо указать коэффициенты при степенях числителя и знаменателя. ‘Inputdelay’ указывает на наличие звена задержки, а через запятую следует время задержки.
z-преобразование полученной передаточной функции осуществляется при помощи команды c2d, причем по умолчанию используется фиксатор нулевого порядка:
Wz=c2d(sys1,20)
Замечание: Найденную z-передаточную функцию методом разложения на простые дроби можно привести к стандартному виду в пакете «Matlab», задав передаточные функции дискретных звеньев и применив команды, соответствующие типу соединения.
Пример.
Пусть z-передаточная функция приведенной системы имеет вид:
.
Необходимо задать каждое из звеньев функции, а затем осуществить их последовательное и параллельное соединение при помощи команд ‘series’ и ‘parallel’ . Для задания передаточной функции в дискретной форме используется синтаксис:
SYS = TF(NUM,DEN,T), где NUM=[k1 k2 k3 …] и den=[n1 n2 n3 …] – коэффициенты при степенях числителя и знаменателя, а T – период дискретизации. Полученную передаточную функцию приведенной системы можно разложить на пять звеньев, три из которых соединены параллельно-согласно
;
;
между собой
и
последовательно со звеньями
и
Тогда последовательность
задания функции будет выглядеть следующим
образом:
sys1=tf([0.7],[1 0 0],20)
sys2=tf([1 0],[1 -1],20)
sys3=tf([-3 0],[1 -0.717],20)
sys4=tf([2 0],[1 -0.607],20)
sys5=tf([1 -1],[1 0],20)
W1=parallel(sys2,sys3)
W2=parallel(W1,sys4)
W=series(W2,sys1)
Wpr=series(W,sys5)
4.5. Расчет настроек дискретных регуляторов в одноконтурной системе
Расчет настроек дискретных регуляторов возможен методом ограничения на частотный показатель колебательности, который задаётся либо определяется по номограммам на основе заданных других показателей качества.
Как было рассмотрено в п. 2.4, это позволяет на комплексной плоскости выделить две области: одну – где обеспечивается необходимый запас устойчивости, соответствующий заданному значению частотного показателя колебательности, вторую – где этот запас устойчивости не обеспечивается, границей является окружность, радиус которой рассчитывается на основе заданного значения частотного показателя колебательности (М) по формуле:
,
центр
окружности определяется координатами
.
Для проведения структурных преобразований и получения дискретной формы описания непрерывной части системы выбирается тип формирователя (фиксатора) и его передаточная функция.
Фиксатор принято относить к непрерывной части, при этом последовательное соединение фиксатора и собственно непрерывной части образует приведенную непрерывную часть. Определившись с приведённой непрерывной частью, находят её z-передаточную функцию (W пр.н.ч.(z)).
Замечание. Для нахождения z-передаточной функции нужно определиться с периодом дискретизации, который достаточно часто выбирают как наибольший общий делитель постоянных времени непрерывной части.
На
основе анализа свойств объекта, а именно
отношения постоянной запаздывания и
постоянной времени объекта
,
выбирается тип регулятора. Если это
отношение меньше 0,2, выбирают
пропорциональный регулятор, если это
отношение имеет пределы от двух десятых
до семи десятых, то пропорционально-интегральный
тип, если более семи десятых, то
пропорционально-интегрально-дифференциальный.
Передаточные функции дискретных регуляторов (Wр-р(z)) приведены в таблице 4.2.
Таблица 4.2. – Передаточные функции дискретных регуляторов
№ |
Тип регулятора |
Передаточная функция |
1. |
Пропорциональный (П) |
|
2. |
Пропорционально-дифференциальный (ПД) |
|
3. |
Пропорционально-интегральный (ПИ) |
|
4. |
Интегрально-дифференциальный (ИД) |
|
5. |
Пропорционально-интегрально-дифференциальный (ПИД) |
|
Замечание. В таблице 4.2использованы стандартные обозначения:
Kр – коэффициент передачи регулятора;
Т – период дискретизации;
Ти – постоянная интегрирования регулятора;
Тд – постоянная дифференцирования регулятора.
Для подбора настроек регулятора (Кр, Ти, Тд) записывается передаточная функция разомкнутой системы в дискретной форме Wр(z):
,
на
основе которой строится амплитудно-фазовая
частотная характеристика (АФЧХ), или
комплексная частотная характеристика
(КЧХ). Её получают заменой переменной
,
в силу периодичности функции
интервал изменения частоты принимают
или
,
или
,
или с учетом симметричности ветвей КЧХ
относительно действительной оси
.
Для
выбранного значения постоянной
интегрирования подбирают такое значения
коэффициента передачи регулятора, при
котором КЧХ разомкнутой системы касается
построенной на основе заданного
частотного показателя колебательности
окружности. Из возможных вариантов
подобранных (Tи,
Кр)
выбирают тот, для которого отношение
окажется наибольшим.
Интервал варьирования постоянной интегрирования может быть выбран на основе анализа постоянной времени [0,5Tоб. наиб.; 1,5Tоб. наиб], который разбивают на 10 – 12 шагов.
Настройки регулятора, обеспечивающие максимальное значение , считаются оптимальными.
Для проверки полученных результатов рассчитывают фактические значения прямых и косвенных показателей качества и сравнивают их с заданными показателями. Если результаты расчетов не хуже заданных, то расчет считается удовлетворительным, если фактические показатели качества оказались хуже заданных, то либо проводят повторный расчет, либо настройки изменяют вблизи найденных значений, добиваясь улучшения показателей качества (прямых и косвенных).
4.6. Пример расчета настроек дискретного регулятора
Рассчитать настройки дискретного ПИ-регулятора для объекта с передаточной функцией
,
если перерегулирование не должно превышать 25%. В качестве метода расчета выбрать метод ограничения на частотный показатель колебательности.
Решение.
Для заданного перерегулирования σ = 25%
последовательно по номограммам определяем
Pmax=1,19;
L=16;
γ = 23; Mдоп
=1,18, при
этом параметры окружности равны
;
.
Анализируя постоянные времени объекта (τ0 = 5с.; Тоб = 20с.), выбираем период дискретизации Т=5с.
Считаем,
что в системе используется фиксатор
нулевого порядка с передаточной функцией
.
Тогда передаточная функция приведенной
непрерывной части имеет вид
.
Для этого выражения находим z-изображение:
.
Используя свойства z-преобразования, получаем формулу для расчета
,
где
.
Для нахождения z-изображения дроби используем приём разложения на простые дроби и таблицу z-изображений (Приложение А):
;
Сравнивая коэффициенты при одинаковых степенях в числителе, составляем систему уравнений для нахождения их:
Решаем систему уравнений, находим коэффициенты:
тогда
,
.
Приводим к общему знаменателю
.
z-передаточная функция приведенной непрерывной части имеет вид:
.
Передаточная функция дискретного ПИ-регулятора имеет вид (таблица 4.2)
.
Передаточная функция разомкнутой системы с учетом последовательного соединения регулятора и приведенной непрерывной части имеет вид:
.
Интервал
варьирования постоянной интегрирования
выбираем по формуле [0,5Tоб.
наиб.;
1,5Tоб.
наиб], т.е.
[0,5∙20; 1,5∙20] = [10;30] с шагом
.
В
передаточной функции разомкнутой
системы заменяем параметр
,
с учетом периодичности экспоненты
частоту при построении АФЧХ изменяем
в пределах
.
На одной комплексной плоскости строим окружность (R) с центром O и АФЧХ разомкнутой системы.
Задаем
первое значение Ти
= 10с.,
подбираем такое Кр,
при котором АФЧХ касается окружности,
Кр
= 0,1, рассчитываем отношение
,
затем берется следующее значение Ти
= 12с. и
подбирается Кр
= 0,118, все результаты расчета сводятся
в таблицу 4.3.
Таблица 4.3. – Результаты расчета настроек регулятора
Tu |
kp |
kp/ Tu |
10 |
0,1 |
0,01 |
12 |
0,118 |
0,009833 |
14 |
0,139 |
0,009929 |
16 |
0,158 |
0,009875 |
18 |
0,166 |
0,010333 |
20 |
0,173 |
0,00865 |
22 |
0,178 |
0,008091 |
24 |
0,182 |
0,007583 |
26 |
0,186 |
0,007154 |
28 |
0,19 |
0,006786 |
30 |
0,193 |
0,006433 |
32 |
0,195 |
0,005472 |
36 |
0,2 |
0,003333 |
На основе таблицы 4.3 можно построить график (рисунок 4.11), либо просто внимательно посмотреть на последний столбец таблицы 4.3.
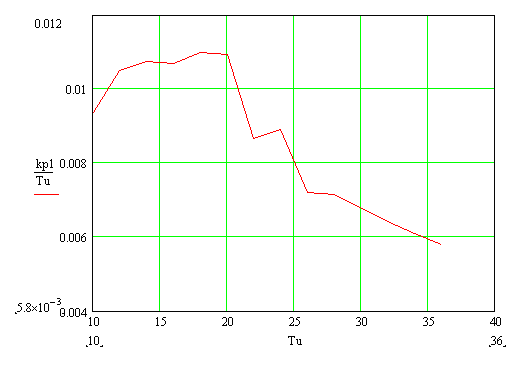
Рисунок
4.11. – Зависимость отношения
от изменения Ти
Наибольшее отношение соответствует значению коэффициента передачи регулятора Кр = 0,198 и постоянной интегрирования Ти = 18с., поэтому их примем за оптимальные.
Для проверки правильности расчета нужно рассчитать прямые и косвенные показатели качества, которые обеспечиваются найденными настройками.
Передаточная функция ПИ-регулятора с найденными настройками имеет вид:
.
Передаточная функция разомкнутой системы:
.
Т.к. обратная связь единичная, то передаточная функция замкнутой системы рассчитывается по формуле:
,
изображение переходной характеристики
.
Переходную характеристику находим обратным преобразованием
.
Амплитудно-частотную характеристику замкнутой системы рассчитываем по формуле:
,
заменив параметр
.
Замечание. Переходную характеристику можно получить простым делением числителя изображения переходной характеристики на знаменатель, т.е.
и
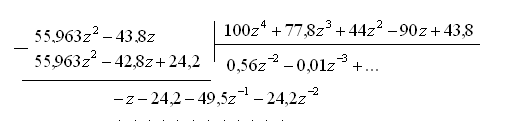
и т.д.
Вид переходной характеристики, прямые и косвенные показатели качества приведены в п. 4.7.
4.7. Расчет настроек дискретных регуляторов в пакете Matlab
Расчет настроек регуляторов требует достаточно громоздких математических расчетов, поэтому целесообразно использование того или иного пакета программ. Они имеют свои достоинства и недостатки по отношению к поставленной конкретной задаче. В данном случае рассмотрим применение для расчета настроек регулятора пакета Matlab.
Как создать М-файл, показано на рисунке 4.12, приведенном ниже.
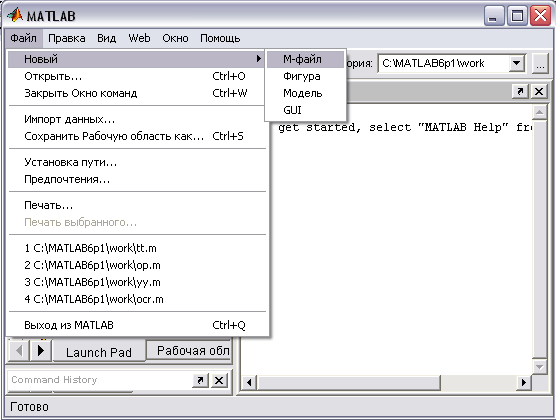
Рисунок 4.12. – Создание нового М-файла
Для
решения данного примера в пакете «Matlab»
сначала необходимо задать полученные
передаточные функции
и
.
z- передаточная функция приведенной непрерывной части системы:
.
W1=tf([10],[20 1]; ‘inputdelay’,5)
Wприв(z) = cd2(W1,5)
Аналогично
в M-файле
MatLab’а
нужно задать и передаточную функцию
ПИ-регулятора в дискретной форме
.
В
общем виде
задается следующим
образом:
Wrr=tf([Kr*(1+T/Ti)
-Kr],[1
-1],T),
где Ti
и Kr
– искомые параметры, задаются в буквенном
обозначении, а T
– период дискретизации. В нашей задаче
T=20с,
,
и в М-файле передаточная функция
регулятора записывается:
Wrr=tf([Kr*(1+20/Ti) -Kr],[1 -1],20)
Передаточная
функция разомкнутой системы в дискретной
форме имеет вид:
.
В М-файле осуществляется
последовательное соединение заданных ранее и :
Wr=series(Wpr,Wrr)
Далее
необходимо задать промежуток изменения
частоты
или
,
где T
– период дискретизации. В рассматриваемом
примере T=20
и, следовательно, частота изменяется в
пределах
.
В М-файле промежуток задается следующим
образом: W=Wmin:h:Wmax,
где Wmin
и Wmax
– границы промежутка, а h
– шаг варьирования (выбирается
произвольно, для достижения оптимальной
точности вычислений берется в сотых
или тысячных долях от граничных значений):
W=0:pi/1000:pi/10
После задания промежутка варьирования частоты необходимо построить КЧХ найденной передаточной функции разомкнутой системы при помощи команды «nyquist», и, удержав полученный график при помощи команды «hold», построить поверх окружность с найденным радиусом и координатами центра (для этой операции следует воспользоваться уже другой командой – «plot»). В комплексной плоскости окружность задается следующим образом:
, где Y – функция окружности, X – варьируемая переменная, и - смещение центра по оси абсцисс и ординат соответственно.
В
рассматриваемом примере мы определили
радиус окружности
и смещение по оси абсцисс
.
В М-файле:
x=0:0.001:10
nyquist(Wrz,W)
hold
R=3.007
Plot(R*((cos(x)–3.458/R)+i*sin(x)))
Задав все команды в М-файл, необходимо сохранить его в рабочей папке «work» под именем команды, которой впоследствии можно будет реализовать все внесенные в него операции. Для этого необходимо в меню «Файл» выбрать «Сохранить как», задать удобное имя, и М-файл по умолчанию будет сохранен нужной папке.
Итоговый М-файл для решения рассматриваемой задачи будет выглядеть, как показано на рисунке (рисунок 4.13).
Рисунок
4.13. – М-файл для решения рассматриваемой
задачи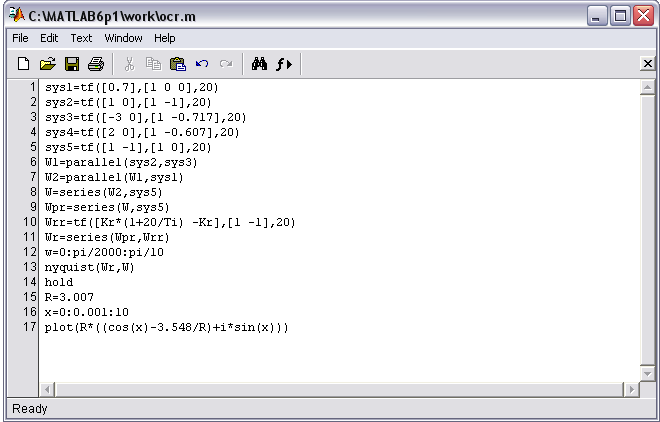
Далее, задавая в командной строке Ti и варьируя Kr, нужно запускать М-файл, набирая его имя в командной строке и нажимая клавишу «Enter». В результате будут получены изображения КЧХ и окружности. Уменьшением или увеличением Kr добиваемся, чтобы КЧХ коснулась окружности. Изображение, как правило, получается сжатым, поэтому целесообразно изменить параметры осей, указав пределы их значений в меню вызываемого пунктом меню «Edit→Axes Properties». Необходимо помнить, что перед тем, как задать новые значения Ti или Kr, нужно закрывать окно графического редактора. Фиксируя значения, при которых произошло касание, заполняем таблицу (см. таблица 4.4). Например Ti=30, Kr=0,5. Запустив М-файл, получаем изображение:
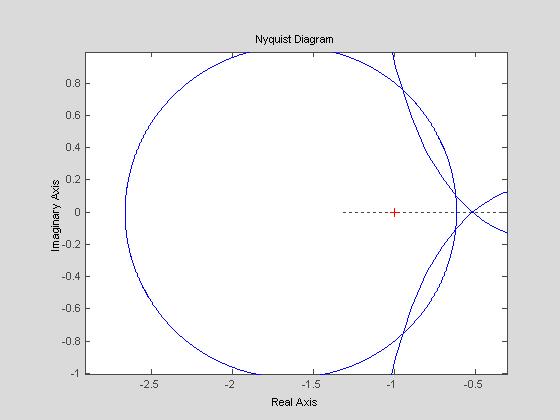
Т.к. КЧХ пересекает окружность, уменьшаем Kr до тех пор, пока касание не произойдет. При Kr=0.41 происходит касание:
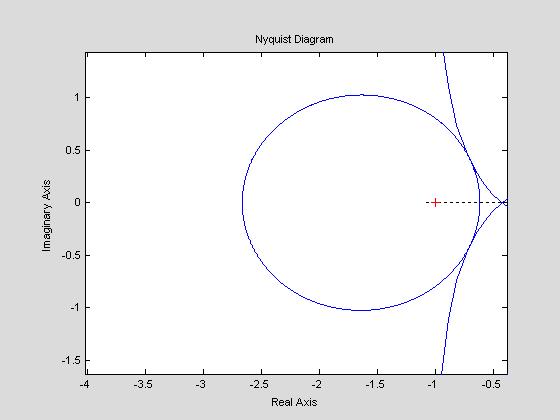
Заносим найденное Kr в таблицу.
Аналогично находим все Kr и Ti и сводим их в таблицу 4.4.
Таблица 4.4. – Значение настроек ПИ-регулятора
-
30
0,410
0,0137
35
0,496
0,0142
40
0,584
0,0146
45
0,679
0,0150
50
0,770
0,0154
55
0,858
0,0156
60
0,945
0,01575
62
0,977
0,01578
65
1,023
0,01574
75
1,166
0,01554
80
1,226
0,01533
85
1,284
0,01511
90
1,34
0,01489
Таким
образом, максимальное
,
при
и
.
При
помощи команды «feedback»
замыкаем единичную обратную связь
параллельно
и строим график реакции на единичное
ступенчатое воздействие (step(Wz,t),
где t
– время, откладываемое по оси абсцисс,
выбирается произвольно для получения
оптимального изображения) :
Wz=feedback(Wr,1)
step(Wz,1000)
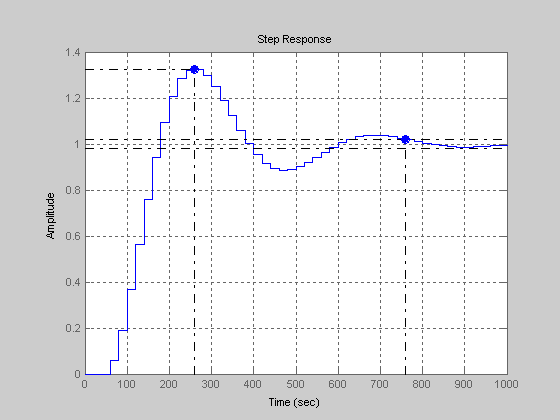
Затем строим АЧХ замкнутой системы:
ffplot(Wz)
Замечание. В пакете MatLab при получении графика переходной характеристики визуально запаздывание увеличивается на один период из-за экстраполяции полученной в периоде ординаты вправо. Что бы получить правильный графический результат, нужно передаточную функцию замкнутой системы домножить на z.
W1=tf([1 0], [1],T)
Wz1=series(Wz, W1)
step (Wz1)
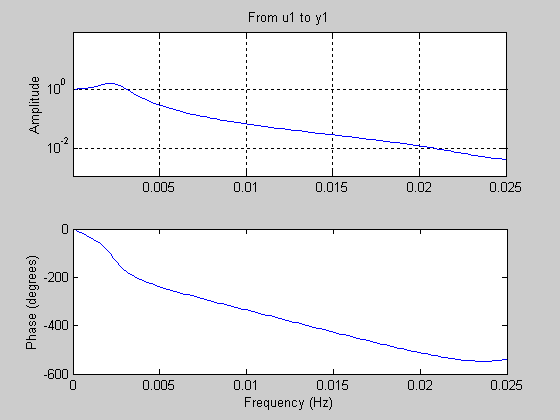
Увеличив изображение при помощи инструмента «Лупа», или же при помощи пункта меню «Инструменты→Статистика» («Tools→Data Statistics» в английской версии программного пакета) находим максимальное значение:
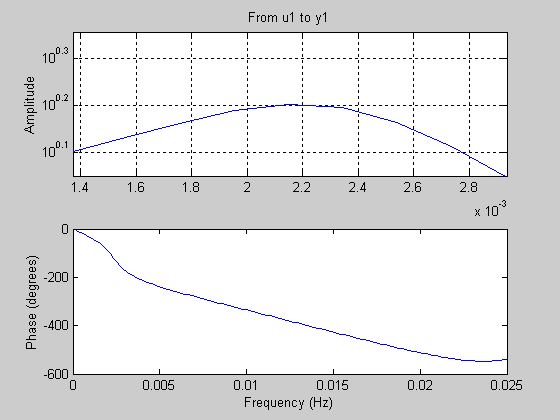
По полученным данным определяются оптимальные показатели качества:
Т. к. полученные показатели качества меньше заданных, расчет удовлетворительный.
4.8. Особенности расчета настроек дискретных регуляторов в многоконтурной системе
При расчете настроек дискретных регуляторов в многоконтурных системах используют последовательность структурных преобразований (п. 3.1 и 3.2), а так же особенности получения z-передаточной функции в зависимости от вида управляющего сигнала (п. 4.3).
Для непрерывного задающего воздействия с учетом неединичных обратных связей в исходной схеме (рисунок 3.7) эти преобразования имеют следующую последовательность.
Для расчета настроек дискретного регулятора (рисунок 4.14).
Рисунок 4.14. – Структурная схема для расчета настроек главного регулятора
Передаточная функция разомкнутой системы для предварительного расчета настроек главного регулятора имеет вид:
.
Расчет настроек дискретного вспомогательного регулятора производится по структурной схеме (рисунок 4.15).
Рисунок 4.15. – Структурная схема для расчета настроек вспомогательного регулятора
Передаточная функция при этом имеет вид:
Уточнение настроек главного регулятора производится по схеме приведенной на рисунке 4.16.
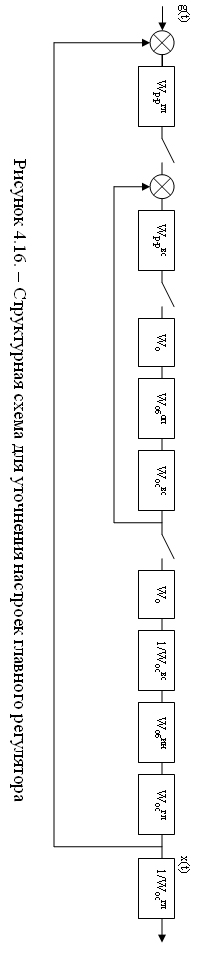
Передаточная функция разомкнутой в точке А системы записывается следующим образом:
.
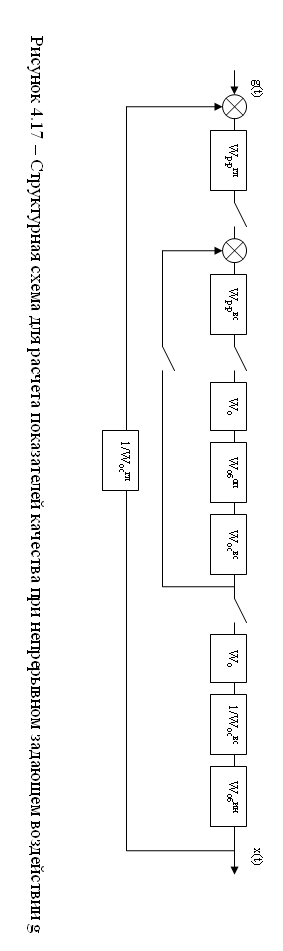
Для построения переходной характеристики и АЧХ замкнутой системы используется исходная схема (рисунок 4.17).
Передаточная функция замкнутой системы для определения прямых и косвенных показателей качества рассчитывается по формуле
.
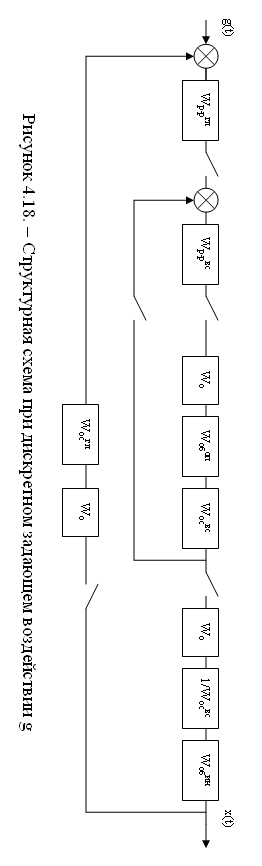
Если задающее воздействие дискретное, то для расчета показателей качества структурная схема имеет другой вид (рисунок 4.18).
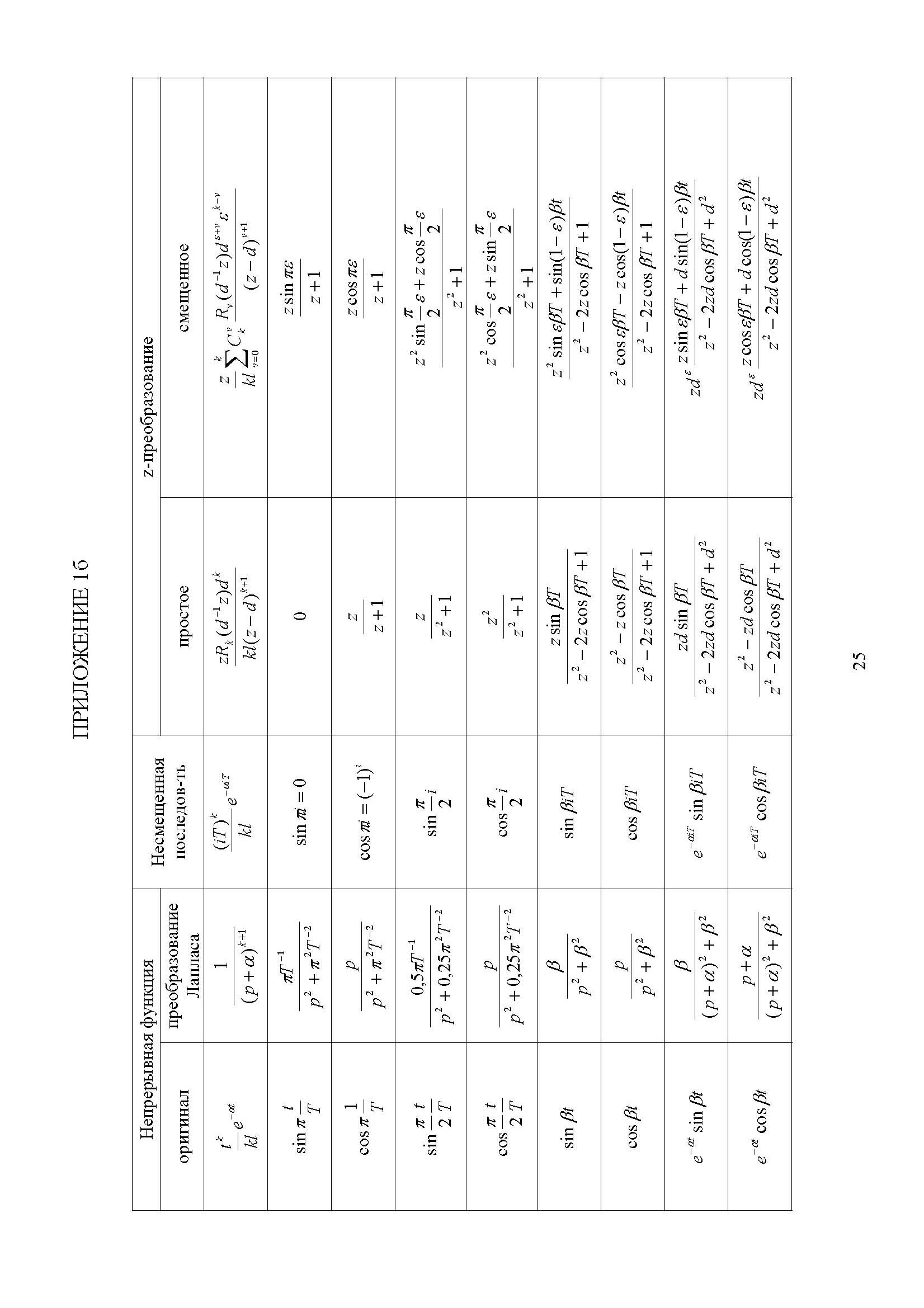
Приложение
А. – Таблица преобразований Лапласа и
z-преобразований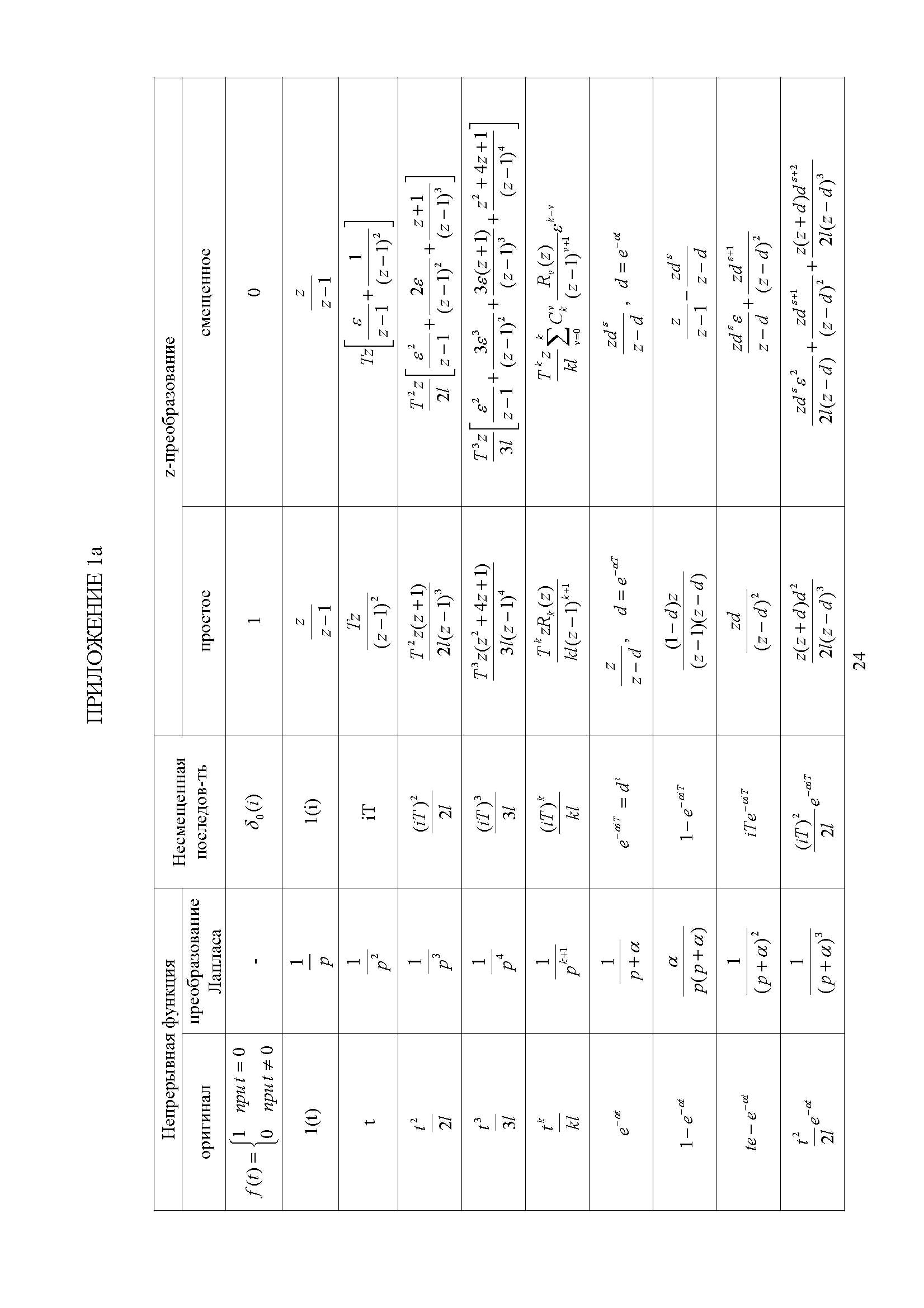
Бесекерский В.А., Попов Е.П. Теория систем автоматического управления – С.-П.: Продукция, – 2003. –743 с.
Воронов А.А. Теория автоматического управления. 4.1. Теория линейных систем автоматического управления – М.:В.Ш., 1986 – 368с.
Теория автоматического управления // Под ред. Нетушисла А.В., 4.1.–М.:ВШ, – 1972 – 372с.
Теория автоматического управления // Под ред. Солодовникова В.В. – Кн 1. – М.: Машиностроение. – 1967 – 411с.
Теория автоматического управления // Под ред. Яковлева В.Б. – М.:В.Ш. – 2003 – 567с.
Ротач В.Я.Теория автоматического управления – М.: МЭИ. – 2004. –387с.
Ротач В.Я.Теория автоматического управления теплоэнергетическими установками – М.: Энергоатомиздат. – 1985
Гудвин Г.К. Гребе С.Ф. Сальгадо М.Э. Проектирование систем управления – М.:Бином – 2004 – 911с.
Дорф Ричард К. Бишон Роберт Х. – Современные системы управления. – М.: Лаборатория базовых значений. – 2004. – 831с.