2.4.7. Расчет настроек непрерывного пи-регулятора в пакете «Matlab»

Решение задачи, приведенной выше, в пакете «Matlab» значительно облегчает нахождение оптимальных настроек регулятора, упрощает построение характеристик системы, нахождение прямых и косвенных показателей качества. Задав нужные передаточные функции и параметры в М-файле приложения, можно избежать многократного повторения операций, что сведет все расчеты к заданию искомых , и выполнению одной единственной команды по реализации М-файла.

Для решения данного примера в пакете «Matlab» сначала необходимо задать исходные передаточные функции и .

Передаточная функция объекта имеет вид:

.

Можно задать каждое из звеньев функции, а затем осуществить их последовательное и параллельное соединение при помощи команд ‘series’ и ‘parallel’ . Для задания передаточной функции используется синтаксис:

Wob =tf ([15],[24 11 1]).

Аналогично в M-файле MatLab’а нужно задать и передаточную функцию ПИ-регулятора .

Wpi=tf([Kr*Ti Kr],[Ti 0])

Передаточная функция разомкнутой системы имеет вид: . В М-файле осуществляется последовательное соединение заданных ранее и :

Wr=series(Wob,Wpi)

Далее необходимо произвольно задать промежуток изменения частоты. В М-файле промежуток задается следующим образом: W=Wmin:h:Wmax, где Wmin и Wmax – границы промежутка, а h – шаг варьирования (выбирается произвольно, для достижения оптимальной точности вычислений берется в сотых или тысячных долях от граничных значений):

W=0:0,001:1000

Далее необходимо построить АФЧХ найденной передаточной функции разомкнутой системы при помощи команды «nyquist», и, удержав полученный график при помощи команды «hold», построить поверх окружность с найденным радиусом и координатами центра (для этой операции следует воспользоваться уже другой командой – «plot»). В комплексной плоскости окружность задается следующим образом:

, где Y – функция окружности, X – варьируемая переменная, и - смещение центра по оси абсцисс и ординат соответственно.

В М-файле:

x=-10:0.001:0

nyquist(Wr,W)

hold

R=3,172

Plot(R*((cos(x)-3,71/R)+i*sin(x)))

Задав все команды в М-файл, необходимо сохранить его под именем команды, которой впоследствии можно будет реализовать все внесенные в него операции. Сделать это можно в меню «Отладка» в строке команд, выбрав «Сохранить и запустить».

Далее, задавая в командной строке T_и и варьируя K_р, нужно запускать М-файл, набирая его имя в командной строке. В результате будут получены изображения АФЧХ и окружности. Уменьшением или увеличением K_р добиваемся, чтобы АФЧХ коснулась окружности. Необходимо помнить, что перед тем, как задать новые значения T_и или K_р, нужно закрывать окно графического редактора. Фиксируя значения, при которых произошло касание, заполняем таблицу (таблица 2.9). Например T_и=30, K_р=1,2. Запустив М-файл, получаем изображение:

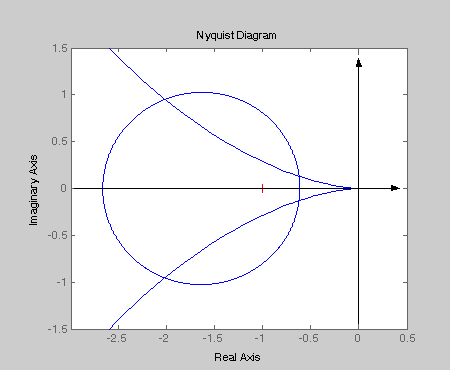
Т.к. АФЧХ пересекает окружность, уменьшаем . Если не касается, то увеличиваем до тех пор, пока АФЧХ и окружность будут иметь только одну общую точку.

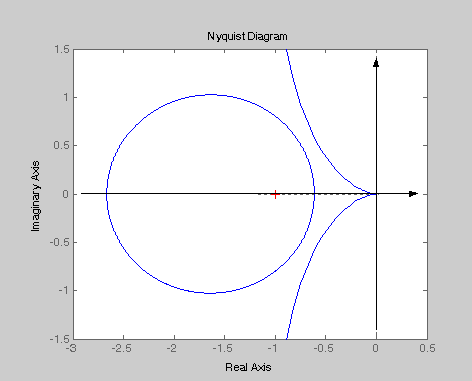
Касание АФЧХ и окружности происходит при .

Найденное K_р заносится в таблицу (таблица 2.9).

Аналогично найдены все остальные значения и таблицы 2.9.

Таким образом, максимальное , при и .

При помощи команды «feedback» замыкаем единичную обратную связь параллельно и строим график АЧХ:

Wz=feedback(Wr,1)

ffplot(Wz)

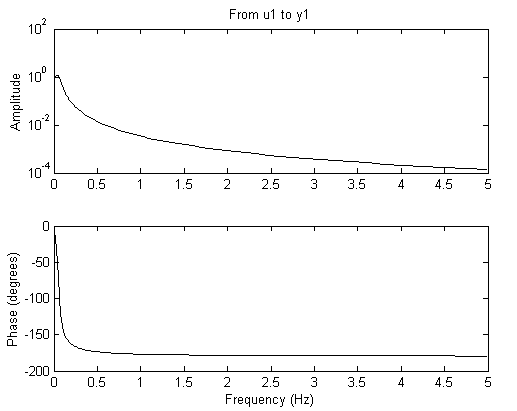
Увеличив изображение, находим максимальное значение:

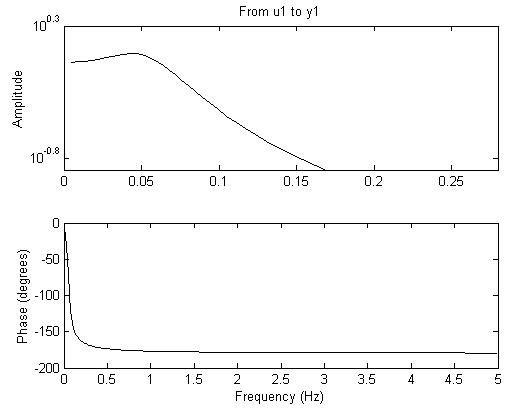
Затем при помощи команды «step» строится реакция на единичное ступенчатое воздействие:

step(Wz)

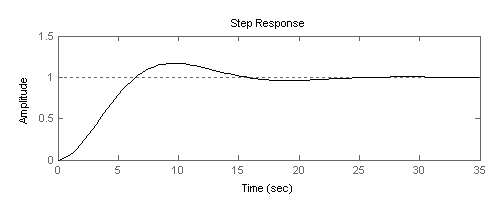
Прямые показатели качества при найденных оптимальных настройках равны:

Т. к. полученные показатели качества не выходят за пределы заданных, расчет можно считать удовлетворительным.