2.4 Расчет настроек непрерывных регуляторов при ограничении на частотный показатель колебательности

2.4.1. Основные сведения

Частотный показатель колебательности М определяется как отношение максимального значения амплитудно-частотной характеристики замкнутой системы (при резонансной частоте) к её значению при ω=0:

,

где ,

– АФЧХ разомкнутой системы,

– АФЧХ замкнутой системы.

Если , то .

Если разомкнутая система астатическая порядка ν (в ней есть одно или несколько интегрирующих звеньев, что соответствует наличию в знаменателе множителя ), то .

Линии равных значений частотного показателя колебательности представляют собой окружности с центром и радиусом

.

Доказательство

Пусть , что справедливо при наличии интегрирующего звена в составе объекта или регулятора; тогда ;

представим АФЧХ разомкнутой системы в первой алгебраической форме комплексного числа:

;

;

.

Используя свойства модуля частного двух комплексных чисел, а именно , частотный показатель колебательности при наличии интегрирующего звена можно записать как:

/

,

что соответствует уравнению окружности:

, где ;

;

.

Т.к. частотный показатель колебательности не должен превышать допустимого значения, то АФЧХ разомкнутой системы не должна заходить в область, ограниченную окружностью, построенной для М_доп, а только касаться её. На этом построен алгоритм подбора настроек регулятора.

2. Алгоритм подбора настроек ПИ – регулятора

Если частотный показатель колебательности системы не задан, а известны прямые показатели качества: перерегулирование и время регулирования t_p, то по номограммам (рисунки 1.19 – 1.21) находят М_доп, определяя его последовательно: по первой номограмме по заданному перерегулированию σ определяют P_max; по найденному P_max находят L и γ ; а по ним М_доп. (по третьей номограмме М ( L; γ)); здесь γ – запас устойчивости по фазе, L ­­– запас устойчивости по амплитуде в децибелах.

Вычисляются координаты центра окружности и её радиус

и строится окружность на комплексной плоскости.

Задаются значениями Т_и и К_р, и для них строится АФЧХ разомкнутой системы

.

Если годограф W_p (jω) заходит в окружность, коэффициент передачи регулятора К_р нужно уменьшить, оставив постоянную интегрирования неизменной, если не касается окружности, то К_р нужно увеличивать до тех пор, пока АФЧХ не коснется окружности.

Выбирается другое значение Т_и2 постоянной интегрирования и подбирается соответствующее значение К_р2.

Все данные заносятся в таблицу (таблица 2.8).

Таблица 2.8 – Значения настроек регулятора

Оптимальными являются те значения, для которых отношение имеет наибольшее значение.

О

птимальные значения и можно определить из графиков или , или (Рисунок 2.11).

а ) б)

Рисунок 2.11. Графики зависимости коэффициента усиления и постоянной времени интегрирования

В первом случае из начала координат проводится касательная с наибольшим наклоном, во втором находится точка экстремума.

2.4.3. Замечания по поводу выбора исходных значений

Начальное может быть вычислено из условия границы устойчивости

Используя свойства комплексных чисел, которые равны только при равенстве действительных и мнимых частей

,

п олучаем два уравнения

с двумя неизвестными и .

Задав произвольное значение и решая их, находят начальные значения и , но можно воспользоваться другой процедурой.

Из опыта известно, что оптимальные настройки не должны значительно отличаться от наибольшей постоянной времени объекта. Поэтому выбирается наибольшая постоянная времени объекта, на её основе строится интервал , задаётся шаг так, чтобы число шагов было не менее , и для каждого из этого интервала проводится процедура подбора .

2.4.4. Проверяется фактическое значение частотного показателя колебательности с выбранными настройками. Для этого:

Записывается передаточная функция регулятора с выбранными значениями коэффициента усиления и постоянной интегрирования

.

Записывается передаточная функция разомкнутой системы

.

Записывается передаточная функция замкнутой системы

.

Оператор заменяется на ( ), вычисляется модуль АФЧХ замкнутой системы

и строится график получившейся АЧХ (рисунок 2.12).

Рисунок 2.12. – График амплитудно-частотной характеристики

По графику определяется фактическое значение частотного показателя колебательности как максимальное значение ординаты (для астатической системы), для статической по формуле М.

Сравниваются получившееся значение частотного показателя колебательности М и допустимое значение; если , расчет удовлетворительный, если нет, то нужно изменить интервал варьирования и провести повторный расчёт.

2.4.5. Особенности расчета настроек ПИД–регулятора

В регуляторе ПИД–типа настраиваемых параметров уже три: коэффициент передачи регулятора , постоянная времени интегрирования и постоянная дифференцирования , т.к. передаточная функция такого регулятора имеет вид

,

.

Для применения известного алгоритма (см. п. 2.4.2) расчета настроек ПИД-регулятора вводится параметр , который задается заранее. Расчет проводится для нескольких значений . Для каждого определяется свое оптимальное значение и среди них выбирается наилучшее с учетом особенностей переходной характеристики.

Для первоначального выбора можно воспользоваться формулой , где - частота, при которой АФЧХ объекта пересекает луч с наклоном , при этом ФЧХ объекта

, т.е. ;

тогда расчётная формула для определения .

Можно определить из графика (рисунок 2.13).

Рисунок 2.13. – Определение по амплитудно-фазовой частотной характеристике объекта

Расчет при выбранном проводят по алгоритму, приведенному в пункте 2.4.2, с той разницей, что передаточная функция регулятора записывается как

и .

2.4.6. Пример расчета

Найти оптимальные настройки ПИ и ПИД–регуляторов в одноконтурной системе, имеющей структурную схему (рисунок 2.8), на основе ограничения на частотного показатель колебательности.

Передаточная функция объекта задана и равна ; допустимое значение перерегулирования .

Решение. По заданному перерегулированию последовательно по номограммам находим , , и расчетное значение частотного показателя колебательности .и расчетныкое значение частотного пам ных00000000000000000000000000000000000000000000000000000000000000000000000000000000000000

Передаточная функция ПИ – регулятора

.

Передаточная функция разомкнутой системы

.

АФЧХ разомкнутой системы ( )

.

Определяем параметры окружности для М_доп=1,17

; ;

; и строим эту окружность (рисунок 2.14).

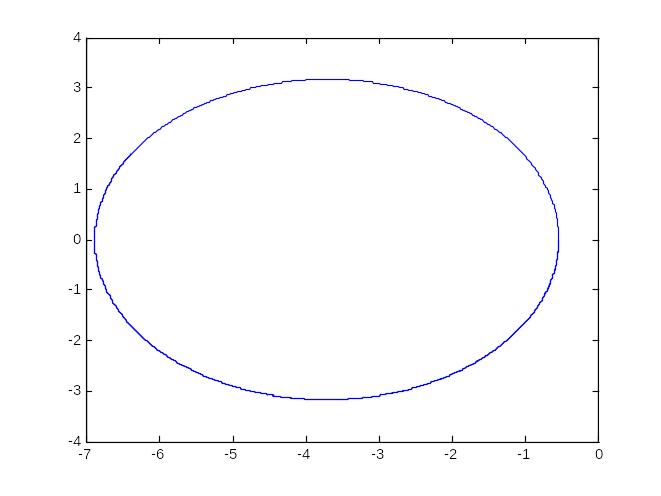
Рисунок 2.14. – Окружность, определяющая запретную зону

Наибольшее значение постоянной времени из передаточной функции объекта T_наиб (3;8) = 8. Создаем интервал варьирования Т_и (4;12) , выбираем шаг h=1; первое значение Т_и=4.

Выбираем произвольное значение К_р, например 0.8, строим АФЧХ согласно формуле

на том же графике, что и окружность (рисунок 2.15).

АФЧХ заходит в окружность (рисунок 2.15.a), К_р уменьшаем, при АФЧХ не касается окружности (рисунок 2.15.б), К_р увеличиваем до тех пор, пока АФЧХ и окружность будут иметь только одну общую точку. Касание АФЧХ и окружности происходит при К_р=0,044 (рисунок 2.15.в).

а)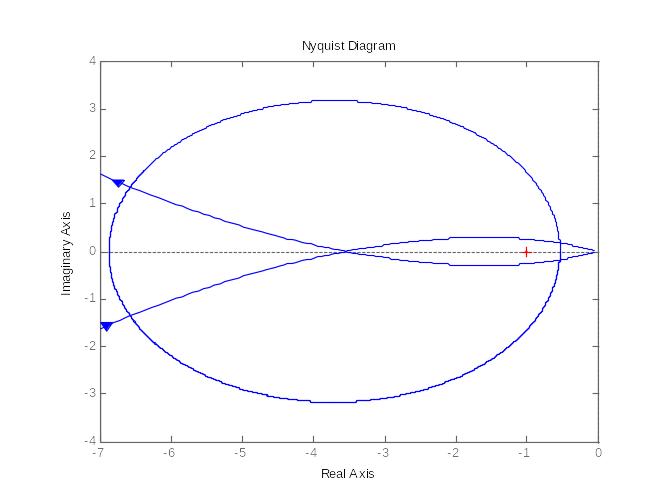

б)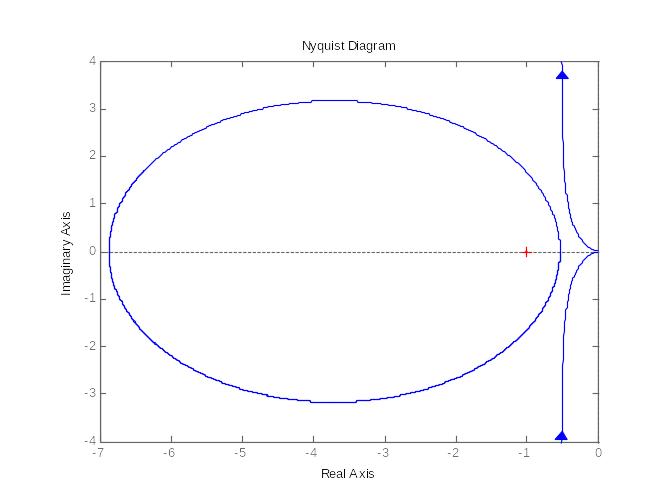

в)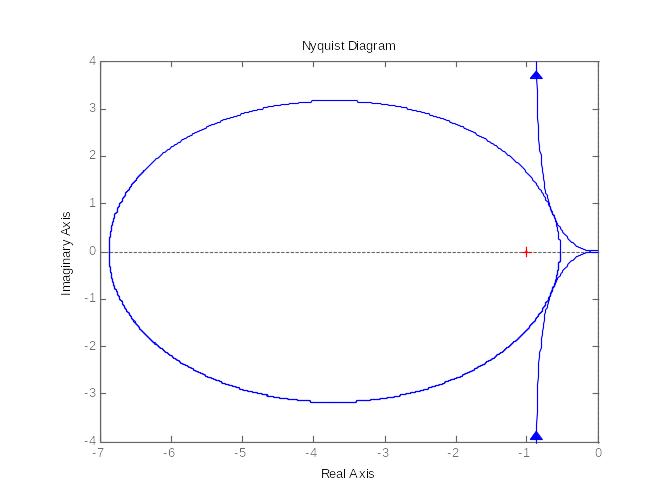

Рисунок 2.15. – Амплитудно-фазовая частотная характеристика разомкнутой системы при различных значениях К_р:

и а) К_р= 0,8

б) К_р= 0,02

в) К_р= 0,044

Следующее значение Т_и =5; повторяем процедуру, К_р=0,073. Процедура повторяется до Т_и = 12.

Найденные значения сведены в таблицу (таблица 2.9).

Таблица 2.9 – Настройки К_р и Т_и Пи-регулятора

Ти	Кр
4,0	0,044	0,011
5,0	0,073	0,0146
6,0	0,11	0,018333
7,0	0,15	0,021429
8,0	0,185	0,023125
9,0	0,215	0,023889
10,0	0,233	0,0233
11,0	0,252	0,022909
12,0	0,27	0,0225

Результаты расчетов представлены в виде графика зависимости отношение от изменения постоянной интегрирования T_и (рисунок 2.16).

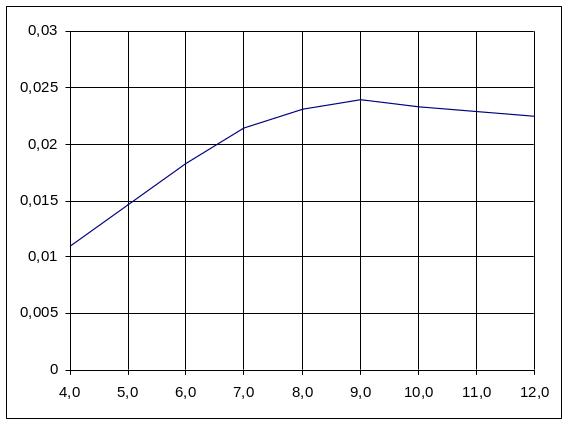
Рисунок 2.16. – Зависимость от

Выбираем те настройки, для которых наибольшее: К_{р опт} = 0.215, Т_{и опт} =9.

Строим АЧХ замкнутой системы

и определяем М_факт = 1,17 (рисунок 2.17).

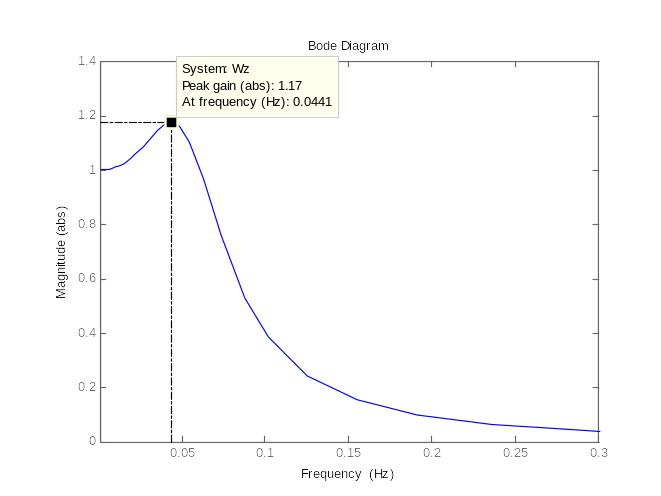
Рисунок 2.17. – Амплитудно–частотная характеристика замкнутой

системы при настройках ПИ-регулятора К_{р опт} = 0,215; Т_{и опт} = 9

Результаты расчётов можно считать допустимыми, т.к. фактическое значение косвенного показателя качества совпало с допустимым значением, т.е. выполняется неравенство , поэтому проверяются прямые показатели качества.

Строим переходную характеристику и определяем прямые показатели качества, используя обратное преобразование Лапласа:

,

график переходной характеристики приведен на рисунке 2.18.

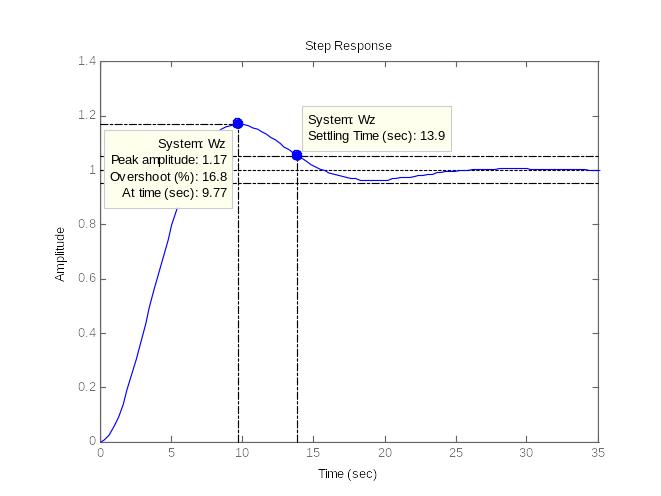
Рисунок 2.18. – График переходной характеристики

Прямые показатели качества составили:

Перерегулирование: σ =16,8%;

Время регулирования: t_p=13,9 с. ≤ 3∙8 = 24с., что соответствует требованиям, предъявляемым к расчету в задании.

Расчет настроек ПИД-регулятора. Для ПИД-регулятора настройки К_р и T_и находятся аналогично.

Определим ; (М_доп=1,17);

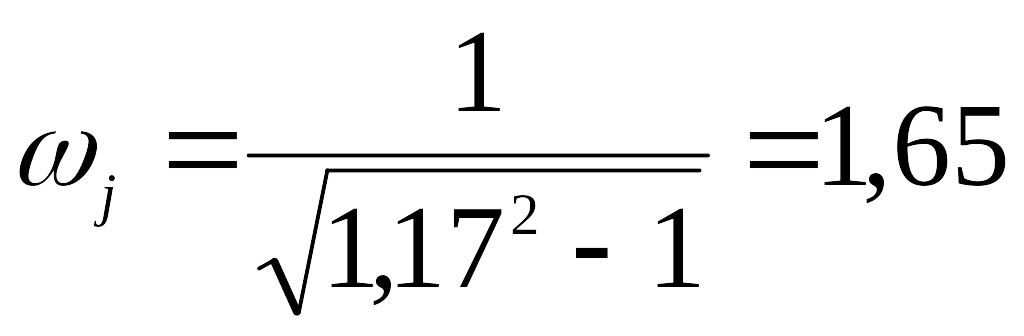, тогда для Т_и = 4

, ;

.

Находим для Т_и=4, α= оптимальное К_р=0,044.

Для Т_и=5 рассчитываем и подбираем К_{р опт} и т.д.

Все расчетные данные сводены в таблицу (таблица 2.10) и приведены на рисунке 2.19.

Таблица 2.10. – Значения настроек ПИД-регулятора

Ти	Кр
4,0	0,044	0,011	0,022957
5,0	0,072	0,0144	0,014692
6,0	0,113	0,018833	0,010203
7,0	0,155	0,022143	0,007496
8,0	0,191	0,023875	0,005739
9,0	0,218	0,024222	0,004535
10,0	0,239	0,0239	0,003673
11,0	0,256	0,023273	0,003036
12,0	0,272	0,022667	0,002551

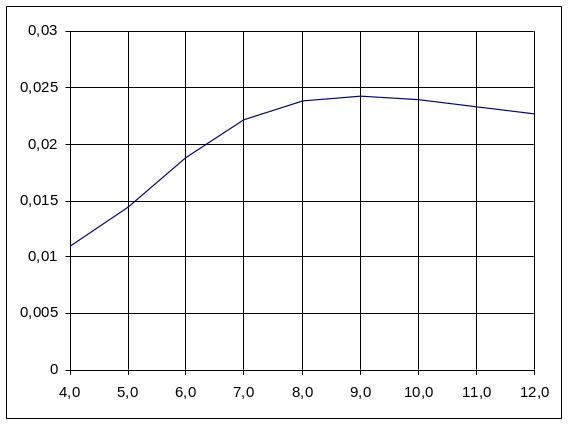
Рисунок 2.19. – Зависимость от

Определяем оптимальные настройки:

К_{р оптс} = 0,218, Т_{и опт} = 9.

Т_{д опт} = αТ_{и опт} = 0,040815,

Т_{б опт} = αγТ_{и опт} = 0,0040815.

Для определения фактического значения частотного показателя колебательности в системе с найденными настройками регулятора строятся АЧХ замкнутой системы, М_факт равно 1,17 (рисунок 2.20).

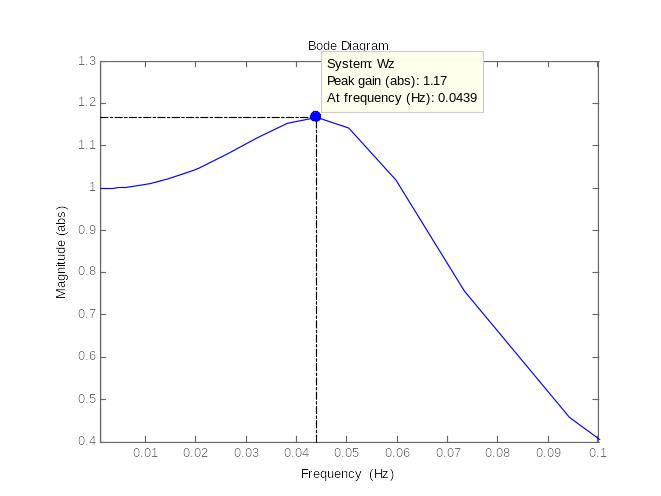
Рисунок 2.20. – Амплитудно–частотная характеристика замкнутой системы при настройках ПИД-регулятора К_{р опт} = 0,218; Т_{и опт} =9

Т.к. фактическое значение косвенного показателя качества совпало с допустимым значением, расчет можно считать удовлетворительным. Проверяем прямые показатели качества.

Для проверки прямых показателей качества строим переходную характеристику, используя обратное преобразование Лапласа (рисунок 2.21):

.

Определяем прямые показатели качества:

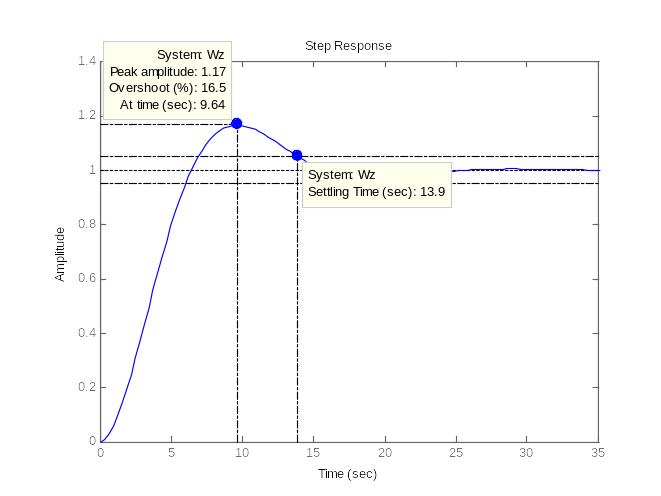
Рисунок 2.21. – Переходная характеристика системы при настройках ПИД-регулятора К_{р опт} = 0,218; Т_{и опт} =9

Прямые показатели качества:

перерегулирование: σ =16,5% ≤ 30%;

время регулирования: t_p=13.9с ≤ 3∙8 = 24с, что соответствует требованиям, предъявляемым к расчету в задании.

Расчет можно считать удовлетворительным, настройки регулятора равны К_{р оптс} = 0,218, Т_{и опт} = 9, Т_{д опт} = 0,041, Т_{б опт} = 0,0040815.