2.2. Расчет регуляторов по кривой отклика

2.1.1. Кривая отклика – реакция системы (изменение выходной величины) на некоторое ступенчатое изменение входной величины.

2.1.2. Получение кривой отклика

а) фиксируется установившееся значение входной и выходной величины (u₀; x₀);

б) в момент времени t₀ изменяется значение u₀ на 10–20% от u₀, т.е. новое значение устанавливается скачком

(1,1–1,2) u₀ = u_1;

в) после окончания переходного процесса измеряется x₁.

2.2.3. Получение характеристик по кривой отклика

а) строится касательная с наибольшим углом наклона;

б) определяется время t₂ пресечения этой касательной и линии x1;

в) вычисляются параметры:

; ₀ = t₁–t₀; (2.3)

, где t₁ – момент времени, в который выходная величина начинает отслеживать изменение управления, приложенное в момент t₀ (t₁>t₀), по кривой отклика определяют как точку пересечения касательной и оси абсцисс, t₂ – значение времени, при котором касательная пересекает линию установившегося значения x₁ (рисунок 2.3).

Замечание. В п. 2.2.3 коэффициент передачи вычислен в абсолютных единицах, он может быть вычислен в безразмерном виде:

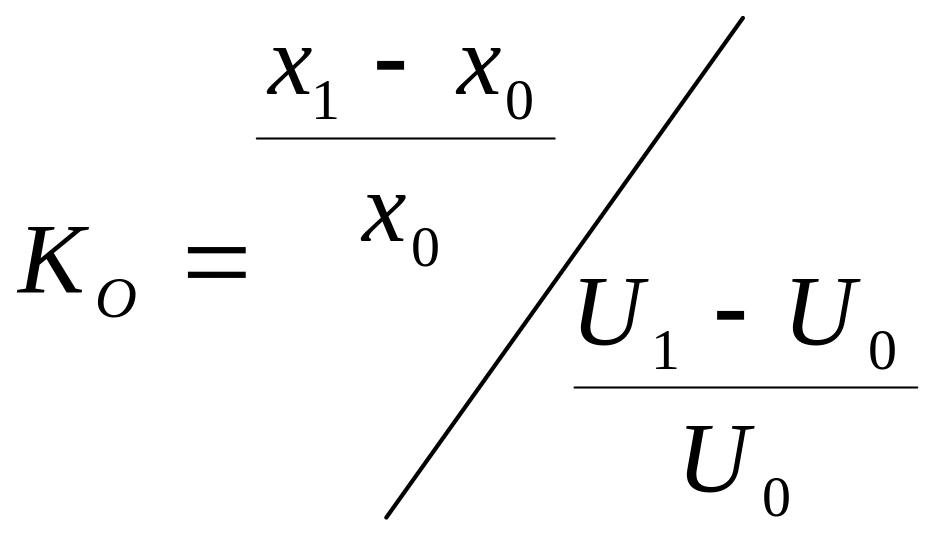. (2.4)

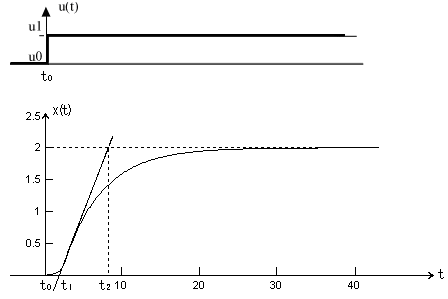
Рисунок 2.3. – Реакция объекта на ступеньку или кривая отклика системы

2.2.4. Алгоритм расчета настроек Зиглера-Никольса по кривой отклика

1. Задаются определенной скоростью затухания переходного процесса x(t), т.е. коэффициентом демпфирования χ ; в данном методе ее принимают равной четырем.

2. Настройки рассчитывают по таблице 2.2.

Таблица 2.2 – Настройки Зиглера – Никольса по кривой отклика

Закон	k	Tu	Tд
П		-	-
ПИ		30	-
ПИД		20	0,50

2.2.5. Настройки регулятора по методу Коэна-Куна по кривой отклика

Таблица 2.3 ­– Настройки Коэна–Куна по кривой отклика

Закон	k	Tu	Tд
П		-	-
ПИ			-
ПИД

Замечание: Перерегулирование и время регулирования в системе в значительной степени зависят от отношения , чем оно меньше, тем больше  и t_p.

Пример 2.2. Подобрать настройки ПИ и ПИД регуляторов по кривой отклика, заданной на рисунке 2.4, методом Зиглера – Никольса и Коэна – Куна, если u₀ = 5; u₁ = 7; объект задан передаточной функцией

.

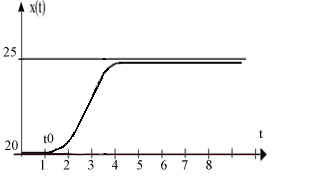
Рисунок 2.4. – Кривая отклика к примеру; t₀ = 1

Построить переходные характеристики, определить и сравнить прямые показатели качества.

Решение. Строим касательную с наибольшим наклоном;

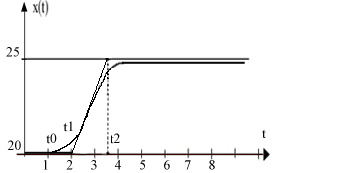
Определим характеристики:

t₀ = 1 (время начала движения x(t));

t₁ = 2;

t₂ = 3,6;

х₀ = 20; х₁ = 25;

;

₀ = t₁– t₀ = 1;

T₀ =υ= t₂ – t₁ = 3,6 – 2 = 1,6;

Рассчитываем настройки ПИ регулятора по таблице 2.2 (Зиглера – Никольса):

;

T_ПИ1 =3·1=3с.

Тогда передаточная функция ПИ – регулятора имеет вид

.

По таблице 2.3 (Коэна – Куна)

;

.

Передаточная функция ПИ – регулятора по методу Коэна – Куна имеет вид

.

Передаточная функция разомкнутой системы для первого регулятора имеет вид

.

Передаточная функция замкнутой системы

.

Изображение переходной характеристики

.

Переходная характеристика вычисляется

.

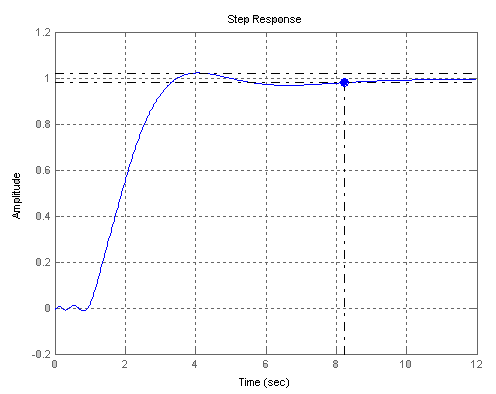
Рисунок 2.5 – Переходная характеристика системы с настройками ПИ – регулятора, подобранными методом Зиглера – Никольса

График приведен на рисунке 2.5, перерегулирование

_ПИ1= 6%, время регулирования t_pПИ1= 8,2с.

Передаточная функция разомкнутой системы с ПИ – регулятором (настройки Коэна – Куна) имеет вид:

,

тогда передаточная функция замкнутой системы

;

;

график приведен на рисунке 2.6.

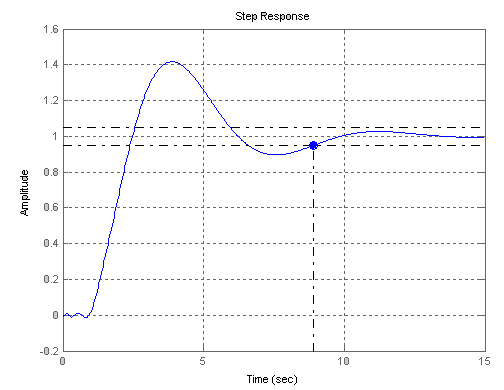
Рисунок 2.6. – Переходная характеристика системы с настройками ПИ – регулятора подобранными методом Коэна – Куна

Перерегулирование в этом случае составило:

_ПИ2= 42%, время регулирования t_pПИ2= 5,65с.

На основе таблиц 2.2 и 2.3 можно рассчитать настройки и других типов регуляторов (П и ПИД).

2.2.6. Решение примера по расчету настроек ПИ-регулятора в командном интерфейсе MatLab

1. Задание передаточной функции объекта в командной строке MatLab можно осуществить следующим образом:

>> Wobj=tf([2.5],[1.6 1],'inputdelay',1)

2. Задание передаточной функции регулятора с найденными по таблице настройками (метод Зиглера-Никольса):

piregZ_N=tf([0.576*3 1],[3 0])

3) Передаточная функция разомкнутой системы рассчитывается с учетом последовательного соединения командой «series»:

Z_Nrazomk=series(piregZ_N,Wobj)

а) Передаточную функция замкнутой рассчитывается с помощью команды «feedback»:

Z_Nzamk=feedback(Z_Nrazomk,1)

б) Реакция на единичное воздействие получается командой «step» (рисунок 2.9):

>> step(Z_Nzamk),grid

С помощью правой кнопки мышки можно выбрать интересующие нас характеристики.

г) Для построения АЧХ системы используется команда «ffplot» (рисунок 2.7).

>> ffplot(Z_Nzamk)

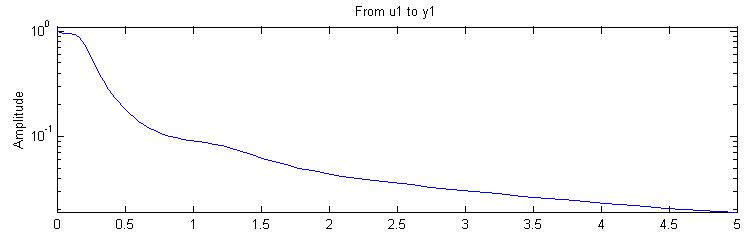
Рисунок 2.7. – АЧХ замкнутой системы: ПИ – регулятор (метод Зиглера – Никольса)

Масштаб можно изменить при помощи пункта Свойства (Properties) контекстного меню, вызываемого щелчком правой кнопкой мыши по изображению графика.

.

Остальные расчеты проводятся аналогично.