2. Определение корней полинома

Для нахождения корней полинома с комплексными коэффициентами

v_nxⁿ + ... + v₂x² + v₁x + v₀

целесообразно использовать функцию polyroots. В отличие от функции root, она не требует начального приближения и возвращает сразу все корни, как вещественные, так и комплексные. Функция Polyroots(v) возвращает вектор длины n, состоящий из корней полинома. Здесь v  – вектор длины n + 1, содержит коэффициенты полинома. Его удобно создать используя команду Symbolic (Символы)  Polynomial coefficients (Коэффициенты полинома). Рис. 19 иллюстрирует определение корней полинома.

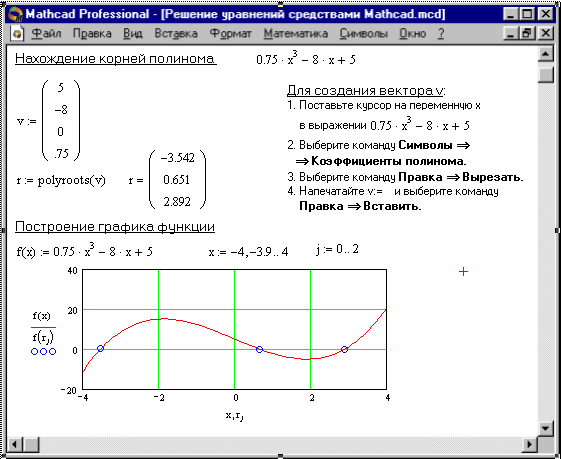
Рис. 19. Определение корней полинома

Задания

4.2.1. Для полиномов g(x) из табл. 7 выполнить следующие действия:

а) с помощью команды Символы  Коэффициенты полинома создать вектор V, содержащий коэффициенты полинома;

б) решить уравнение g(x) = 0 с помощью функции polyroots;

в) решить уравнение символьно, используя команду Символы  Переменные  Вычислить.

Таблица 7

№	g(x)	№	g(x)
1	x4 - 4x3 + 7x2 - 2x + 10	2	x4 + x3 - 17x2 - 45x - 100
3	x4 + 5x3 + x2 - 3x – 40	4	x4 - 5x3 + x2 - 15x + 50
5	x4 - 16x2 - 47x – 57	6	x4 - 4x3 - 2x2 - 20x + 24
7	x4 - x3 + 2x2 - 21x + 17	8	x4 + 5x3 + 6x2 + 7x - 19
9	x4 - x3 - 19x2 - 61x -120	10	x4 - 7x3 + 6x2 - 5x + 120
11	x4 + 6x3 + 7x2 + 12x – 23	12	x4 + 10x3 +32x2 +70x+ 75
13	x4 + 5x3 - 43x2 - 45x -147	14	x4 + 7x3 + 27x2 + 59x+ 60
15	x4 - 6x3 + 3x2 + 12x + 67	16	x4+13x3+21x2+45x+17

3.Решение систем нелинейных уравнений

MathCAD дает также возможность численно решать также и системы нелинейных уравнений с помощью функции Find(z1, z2, . . .,zn), которая возвращает приближенное решение системы уравнений с числом уравнений равным числу неизвестных..⁵ Это число должно быть равно числу аргументов функции Find.

Решение проводится в следующем порядке:

• Задать начальное приближение для всех неизвестных, входящих в систему уравнений.

• Напечатать ключевое слово Given. Оно указывает MathCAD, что далее следует система уравнений.

• Ввести уравнения и неравенства в любом порядке с использованием знаков логических операций между их левыми и правыми частями знаков =, <, >, ,  палитры Boolean (Логический) Для печати символа = ⁶ можно использовать сочетание клавиш Ctrl+”=”

• Ввести выражение, которое включает функцию Find, например:

а:=Find(х, у).

Пример на рис. 20 иллюстрирует решение системы уравнений

Для нахождения начального приближения преобразуем уравнения системы к виду f ₁(x) = y и f ₂ (y)= x

В документе MathCAD построим графики функций f ₁(x) = y и f ₂ (y)= x и найдем окрестность точки пересечения.

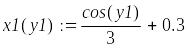
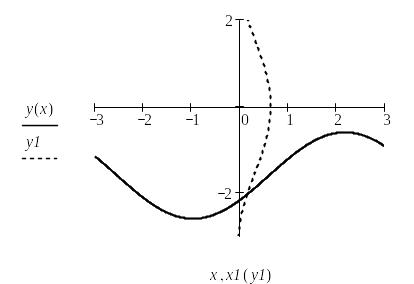
Рис. 20. Определение начального приближения для решения системы уравнений

В качестве начального приближения можно взять произвольную точку из этой окрестности. Затем записывается вычислительный блок Given - Find, находится решение и делается проверка (рис. 21).

_{Начальное приближение}

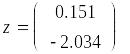
Проверка

Рис. 21. Решение системы нелинейных уравнений

Ключевое слово Given, уравнения и неравенства, которые следуют за ним, и какое–либо выражение, содержащее функцию Find, называют блоком решения уравнений.

В блоке решения недопустимо использовать следующие выражения:

• Ограничения со знаком .

• Дискретный аргумент или выражения, содержащие дискретный аргумент в любой форме.

• Неравенства вида a < b < c.

Блоки решения уравнений не могут быть вложены друг в друга, каждый блок может иметь только одно ключевое слово Given и имя функции Find.

Используя функцию Find можно произвести следующие три действия:

• Вывести найденное решение, напечатав выражение вида:

Find(var1, var2,…,varn) =

• Определить скалярную или векторную переменную с помощью функции Find, если требуется использовать решение системы уравнений в дальнейших расчетах:

a := Find(x) – скаляр,

x := Find(var1, var2,…) – вектор.

• Определить новую функцию с помощью Find:

f(a, b, c, …) := Find(x, y, z, …).

Эта конструкция удобна для многократного решения системы уравнений при различных значениях некоторых параметров a, b, c,…, входящих в систему уравнений.

Если после многих итераций не найдено подходящего решения, то MathCAD выводит сообщение об ошибке (Решение не найдено). Оно может быть вызвано следующими причинами:

• Система не имеет решения.

• Для уравнения, которое не имеет вещественных решений, в качестве начального приближения взято вещественное число и наоборот.

• В процессе поиска решения последовательность приближений попала в точку локального минимума невязки.

• Возможно, поставленная задача не может быть решена с заданной точностью. Попробуйте увеличить значение TOL.

Еще одну возможность поиска решения дает применение функции ункция Minerr, использующей тот же алгоритм, что и Find. Если в результате поиска не может быть получено дальнейшее уточнение текущего приближения к решению, Minerr возвращает это приближение. Функция Find в этом случае возвращает сообщение об ошибке. Правила использования функции Minerr такие же, как и функции Find: Minerr(z1, z2, . . .) . Число аргументов должно быть равно числу неизвестных. Если Minerr используется в блоке решения уравнений, необходимо всегда включать дополнительную проверку достоверности результатов.

Задание.

4.3.1. Преобразовать нелинейные уравнения системы (табл. 8) к виду f ₁(x) = y и f ₂ (y)= x. Построить их графики и определить начальное приближение решения.  Решить систему нелинейных уравнений с помощью функций Find и Minerr.

Таблица 8

№	Система уравнений	№	Система уравнений
1		2
3		4
5		6
7		8
9		10
11		12
13		14
15		16