2. Графики в полярной системе координат

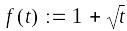
а

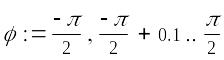
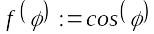
б

Рис. 8. Примеры графиков в полярной системе координат

Графики в полярной системе координат (рис.8) строятся аналогично декартовой системе. Шаблон выводится с помощью кнопки палитры Графики. В нем указываются (рис. 8): слева – функция, задающая зависимость радиуса от угла, внизу – имя угловой переменной, изменяющейся от 0 до 360, справа снизу и сверху – минимальное и максимальное значение радиуса. На рис. 8 а) аргумент функции меняется от 0 до , а на рис. 8 б) – от до .

Задания.

2.2.1. Построить следующие замечательные кривые [6] в полярной системе координат, используя уравнения (а) и в декартовой системе координат, используя уравнения (б). Значения параметров кривых указываются преподавателем.

1. Строфоида (название дано Миди в 1849 г. от греческого “строфе” – поворот) а) б) ;

2. Циссоида Диокла (греческий ученый II в. до н.э.). Название дано от греческого “киссос” – плющ, при замыкании центральной части линии полуокружностью получается фигура, напоминающая лист плюща

а) б) ;

3. Декартов лист (кривая предложена Декартом в 1638 г., название дано в XVIII веке) а) б) ;

4. Верзьера Аньези (названа именем итальянского математика Марии-Гаэтаны Аньези, которая рассматривала эту линию в широко распространенном в XVII в. руководстве по высшей математике). Термин верьзера дан итальянским ученым Гвидо Гранди от словосочетания sinus versus (обращенный синус).

б) ;

5. Конхоида Никомеда (древнегреческий ученый, живший в 260-150 гг. до н.э., название дано по сходству с раковиной, от греческого “конхе” – раковина). Следует отдельно рассмотреть случаи:

а) б) ;

6. Улитка Паскаля (названа французским ученым Г.Персонье, работавшим под псевдоним Роберваль, в честь Э.Паскаля, отца известного ученого Блеза Паскаля)

а) б) ;

7. Линия Кассини (предложена астрономом Джиованни Кассини (1625-1712 гг.)

а) ;

8. Лемниската Бернулли (предложена в 1694 г. основоположником теории вероятностей Яковом Бернулли и названа от греческого - шерстяная повязка)

а)

б) ;

9. Apxимедова спираль (впервые изучена великим греческим ученым Архимедом в III в. до н.э.)

а) ;

10. Эвольвента (развертка) круга - линия, описываемая концом натянутой нити, сматываемой с круглой катушки радиуса

а) ,

б) ;

11. Логарифмическая спираль а) ;

12. Циклоида –линия, которую описывает точка, взятая на расстоянии от центра круга радиуса , когда он катится без скольжения по прямой б) ;

13. Эпициклоиды– линии, которые описывают точки круга радиуса , когда этот круг катится без скольжения по направляющей окружности радиуса с ее внешней стороны

б) ;

14. Гипоциклоиды – линии, которые описывают точки круга радиуса , когда этот круг катится без скольжения по направляющей окружности радиуса с ее внутренней стороны

б) ;

15. Трактриса (названа Гюйгенсом от латинского trahere – тянуть, увлекать)

б) ;

16. Цепная линия – линия, по которой провешивается однородная нерастяжимая нить, закрепленная в двух ее концах

б) ;

17. Фигуры Лиссажу образуются при сложении двух гармонических колебаний во взаимно перпендикулярных направлениях, значения частот и фазы указываются преподавателем.

.