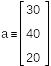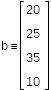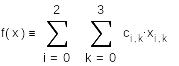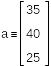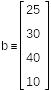2. Действия с матрицами

Система MathCAD позволяет выполнять различные действия с матрицами так же легко, как с обычными переменными. Ниже приведены задания на вычисление полиномов от матриц и определителей матриц.

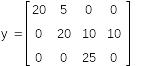
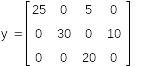
7.2.1. Найти значение многочлена от матрицы А.

1)

2)

3)

4)

5)

6)

7)

8)

9)

10)

11)

12)

13)

14)

15)

16.

17)

18)

19)

20)

7.2.2. Вычислить определитель.

1) ; 2) ; 3) ;

4) ; 5) ; 6) ;

7) ; 8) ; 9) ;

10) ; 11) ; 12) ;

13) ; 14) ; 15) ;

16) ; 17) ; 18) ;

19) ; 20) ; 21) ;

22) ; 23) ;24) ;

7.2.3. Решить задания (П4)1-3, 11 из [4].

8. Линейное программирование

Линейным программированием называют решение задачи оптимизации линейных функций при линейных относительно неизвестных ограничениях (неравенствах и равенствах) [4,9]. Рассмотрим пример транспортной задачи.

1. Транспортная задача

Сущность транспортной задачи (называемой также задачей о назначениях) состоит в минимизации целевой функции

, (1)

представляющей собой стоимость перевозки сырья из m пунктов поставки в n пунктов потребления, причем - стоимость перевозки (тариф), а  объем перевозок от i -го поставщика j-му потребителю. Поиск неотрицательных значений переменных (назначений) ведется при n+m ограничениях запасов сырья в пунктах поставки

, (2)

и запросов потребителей

. (3)

Если сумма запасов равна сумме потребностей, то имеет место задача с закрытой моделью

. (4)

Условиям рыночной экономики более соответствует открытая модель, в которой запасы поставщиков не равны запросам потребителей.

Решение закрытой транспортной задачи для n=2, m=3 приведено ниже. Напомним, что при вводе условий используется знак логического равенства с палитры Boolean (Логический).

Транспортная задача

Тарифы - стоимости перевозки единицы продукта от 1 поставщика потребителям 1, 2, 3

стоимости перевозки единицы продукта от 2 поставщика потребителям 1, 2, 3

Количество продукта у 1 и 2 поставщиков

Запросы потребителей 1,2,3

Общие затраты на перевозку (целевая функция)

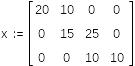
Начальное приближение

Вычислительный блок начинается с ключевого слова Given:

Условие равенства вывозимого продукта запасам у 1 и 2 поставщиков

Условие равенства доставленного продукта потребностям 1, 2 и 3 покупателей

Условия неотрицательности объема поставок

Минимизация:

Ответ:

Объемы поставок: Потребители 1 2 3

Поставщик 1

Поставщик 2

Минимальные затраты на перевозок

Эта задача, была решена ранее с помощью табличного процессора Excel 2000 [10]. Сравнение двух способов решения демонстрирует преимущества системы MathCAD.

Для решения иной транспортной задачи достаточно изменить числовые значения в данных документах MathCAD и выполнить команду Math (Математика, Просчитать документ). Имеющихся текстовых пояснений достаточно, чтобы имея только один этот документ, можно было бы легко решить и другие подобные задачи.

При решении оптимизационных задач с большим числом переменных целесообразно использовать матрицы. В них с помощью палитры матричных операций, показанной на рис. 2, размещаются тарифы перевозок, начальные приближения для объемов перевозок, запасы поставщиков и потребности потребителей. Целевая функция записывается с помощью соответствующие палитры шаблона суммирования (рис. 2). В качестве примера рассмотри задачи, решенные ранее в статье [10] с помощью табличного процессора Excel. Для них приведены тексты документов MathCAD, сохраненные в формате rtf и вставленные в документ Word. Сравнение двух способов решения демонстрирует преимущества системы MathCAD.

Решение закрытой транспортной задачи с тремя поставщиками и четырьмя потребителями имеет следующий вид.

Документ MathCAD	Пояснения
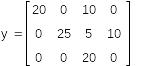
Закрытая транспортная задача Тарифы - стоимость перевозки продукта от поставщиков 1, 2, 3 потребителям 1, 2, 3,4	При наборе выражения использован символ глобального присваивания  из палитры Вычисления на рис.2, позволяющий определять переменные в любом месте документа. Матрица с 3 строками (поставщики) и 4 столбцами (потребители) вводится с помощью палитры Матрицы или с помощью команды Вставка, Матрица… . Так можно и добавлять строки и столбцы в уже имеющиеся матрицы и стобцы.
Запасы продукта у поставщиков 1,2 и 3 Потребности потребителей 1,2,3,4	Использованы символ глобального присваивания  и вставка матриц с одним столбцом и тремя строками для поставщиков и четырьмя для потребителей.
Общие затраты на перевозку (целевая функция)	При вводе целевой функции использован шаблон суммы из панели Матанализ (рис.2). Индексы вводятся после нажатия клавиши [.
Начальное приближение	Использованы символ локального присваивания := и вставка матрицы с 3 строками (поставщики) и 4 столбцами (потребители)
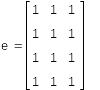
Вспомогательная матрица	Введена вспомогательная матрица с единичными элементами, число столбцов которой равно числу поставщиков, а число строк – числу потребителей. Вывод ее значений, осуществляемый с помощью знака равенства =, не обязателен для решения задачи. Символ перечисления .. вводится нажатием клавиши ; или с помощью знака перечисления значений дискретной величины m..n палитры Матрицы
Ограничения: равенство вывозимого продукта запасам у поставщиков	Вычислительный блок начинается с ключевого слова Given (в переводе с англ. произведено). Первое ограничение записывается в виде булевского равенства = первого столбца (с номером 0) произведения матриц х и е столбцу а. Выделение столбца осуществляется с помощью знака М<> палитры Матрицы
равенство вывозимого продукта потребностям потребителей	Здесь дополнительно использована операция транспонирования (замена местами строк и столбцов) произведения матриц х и е с помощью знака МТ палитры Матрицы
Условия неотрицательности объема поставок	Знак больше или равно находится на палитре Матрицы
Минимизация: Ответ: Минимальные затраты на перевозку	Функция Minimize находит значения объемов перевозок, соответствующих минимуму целевой функции.

Для перехода к решению открытых транспортных задач с объемом запасов у поставщиков, не равным потребности потребителей, в документе делаются изменения, например:

Закрытая задача	Открытые задачи
Запасы равны потребностям	Запасы больше потребностей	Потребности больше запасов
Запасы продукта у поставщиков 1,2 и 3 в сумме равны потребностям потребителей 1,2,3,4	Запасы продукта у поставщиков в сумме превышают потребности потребителей	Запасы продукта у поставщиков в сумме меньше потребности потребителей
Ограничения: равенство вывозимого продукта запасам у поставщиков	Ограничения: количество вывозимого продукта меньше запасов у поставщиков	Ограничения: равенство вывозимого продукта запасам у поставщиков
равенство вывозимого продукта потребностям потребителей	равенство вывозимого продукта потребностям потребителей	количество вывозимого продукта меньше потребностей потребителей
Ответ: Минимальные затраты на перевозку	Ответ: Минимальные затраты на перевозку	Ответ: Минимальные затраты на перевозку