4. Определение точек экстремума функций одной и двух переменных

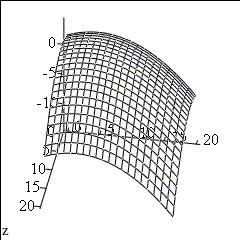
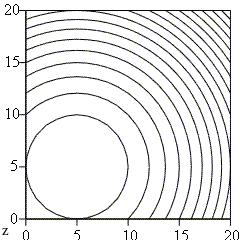
Поиск минимальных или максимальных значений функции при заданных ограничениях называют задачами оптимизации. Для предварительного анализа функций и поиска их экстремумов полезно построение двумерных графиков (для функций одной переменной) или поверхностей и контуров (для функций двух переменных). Примеры поверхности и линий уровня функции

показаны на рис. 22 а) и б) соответственно. По ним легко определить примерное положение максимума этой функции.

а

б

Рис. 22. Поверхность (а) и линии уровня (б) функции z(a,b)

Решение оптимизационной задачи при ограничениях

приведены в документе MathCAD с блоком Given:

_{Поиск максимума функции двух переменных}

_{Начальное приближение}

_{Ограничения:}

_Ответ: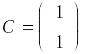

Решение более простых задач можно записать в кратком виде:

_{Поиск минимума функции одной переменной}

Задания.

4.4.1. Определите приближенно точки экстремума функции , где функции берутся из табл. 6. В начале решения построить график , затем сделать проверку.

4.4.2. Для функции , где и - левые части систем из табл. 8, построить поверхности и линии уровня, определить начальное приближение для поиска точки экстремума и найти ее, сделать проверку.

5. Математический анализ, символьные вычисления

1. Вычисление определенных интегралов

Вычисление определенных и кратных интегралов производится с помощью знаков математической палитры Calculus, примеры показаны в документе MathCAD

_{, ,}

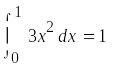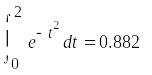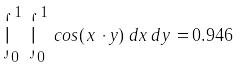
Задания.

5.1.1. Вычислить определенные интегралы от функций из табл. 1, 2, 6,7.

5.1.2. Построить фигуры в заданиях 12.1-12.30 из [4] и найти их площади.

5.1.3. Найти дневную выработку Р

за рабочий день продолжительностью восемь часов, если производительность труда в течение дня меняется по эмпирической формуле

где =1 час. Построить график зависимости производительности труда от времени, найти ее максимум.

5.1.4. Вычислить двукратные интегралы от функций из табл. 5 и задания 4.4.2.

2. Вычисление неопределенных интегралов

Вычисление неопределенных интегралов производится также с помощью знаков математической палитры Calculus с набором в конце символьного знака равенства 

_{, ,}

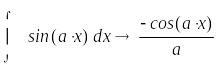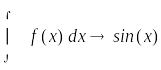
_{Задания}

5.2.1. Вычислить неопределенные интегралы из табл. 9.

Таблица 9

№	Интеграл	№	Интеграл	№	Интеграл
1		2		3
4		5		6
7		8		9
10		11		12
13		14		15
16		17		18

5.2.2. Вычислить интегралы от функций из заданий 11.1-12.20 из [4].

3. Дифференцирование

_{Символьное дифференцирование и построение графика четвертой производной показано в документе MathCAD и на рис. 23:}

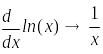
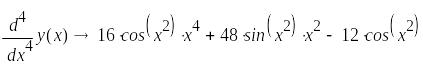
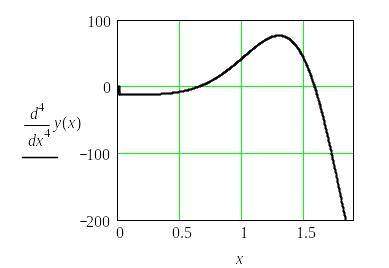
Рис. 23. Примеры дифференцирования и построения графика производной

Задания.

5.3.1. Вычислить производные первого и выше порядка от функций из табл. 1, 2, 6, 7.

5.3.2. Найти первые и вторые производные функций из табл. 10. Построить их графики.

Таблица 10

№	f(х)	№	f(х)	№	f(х)
1		2		3	(2x + 3) sin x
4		5		6	2
7		8	2	9	1/(1 + x + x2)
10		11	(x + 1) sin x	12
13	x2 	14	5x + x lg x	15

5.3.3. Вычислить производные первого и выше порядка от функций из заданий 11.1-12.20 из [4].

5.3.4. Найти первые и вторые производные в заданиях 8.1-8.26, (П2.) 3.1-3.10 из [4].