По предприятиям легкой промышленности региона получена информация, характеризующая зависимость объема выпуска продукции (Y, млн.руб.) от объема капиталовложений (X, млн.руб.)

Требуется:

1. Постройте поле корреляции и сформулируйте гипотезу о форме связи.

2. Найти параметры уравнения линейной регрессии и дать ему экономическую интерпретацию.

3. Оценить тесноту связи с помощью показателей корреляции и детерминации.

4. Проверить значимость уравнения регрессии с помощью F-критерия Фишера (α=0,05) и с помощью средней относительной ошибки аппроксимации. Сделать вывод о качестве модели.

5. Рассчитайте параметры уравнений гиперболической, степенной и показательной регрессий.

6. Для указанных моделей рассчитайте индексы корреляции и детерминации, оцените значимость регрессий с помощью F-критерия Фишера и средней относительной ошибки аппроксимации. Сделайте выводы.

7. С помощью сравнения основных характеристик выберите лучшее уравнение регрессии и сделайте вывод.

8. Осуществите прогнозирование среднего показателя Y при уровне значимости α=0,05, если прогнозное значение фактора Х составит 80% от его максимального значения. Определите доверительный интервал прогноза.

Вариант 8.

Х	10	25	56	38	23	66	34	75
У	7	22	30	29	15	32	22	39

Построение линейной модели парной регрессии .

Рабочая таблица.

N	X	y	x2	xy	y2
1	64	64	4096	4096	4096	60,2	3,84	0,0600
2	68	56	4624	3808	3136	58	-1,96	0,0350
3	82	52	6724	4264	2704	50,3	1,74	0,0334
4	76	48	5776	3648	2304	53,6	-5,56	0,1158
5	84	50	7056	4200	2500	49,2	0,84	0,0168
6	96	46	9216	4416	2116	42,6	3,44	0,0747
7	100	38	10000	3800	1444	40,4	-2,36	0,0621
Сумма	570	354	47492	28232	18300		-0,02	0,3979
Среднее	81,43	50,57	6784,57	4033,14	2614,29			0,0568

Значения параметров а и b линейной модели определим, используя данные таблицы

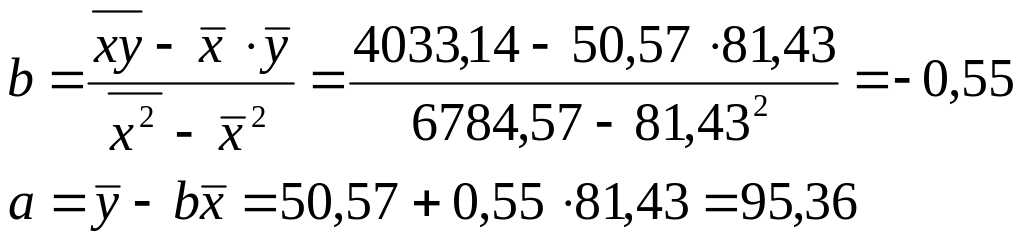
Уравнение линейной регрессии имеет вид:

С увеличением объема капиталовложений на 1 млн.руб. объем выпускаемой продукции уменьшится в среднем на 550 тыс.руб. Это свидетельствует о неэффективности работы предприятий, и необходимо принять меры для выяснения причин и устранения причин и устранения этого недостатка.

3.Рассчитаем линейный коэффициент парной корреляции по следующей формуле:

Можно сказать, что связь между объемом капиталовложений Х и объемом выпуска продукции У обратная, достаточно сильная.

Рассчитаем коэффициент детерминации: R_yx=r²_yx=0,822

Вариация результата У (объем выпуска продукции) на 82,2% объясняется вариацией фактора Х (объемом капиталовложений).

4.Оценку значимости уравнения регрессии проведем с помощью F-критерий Фишера:

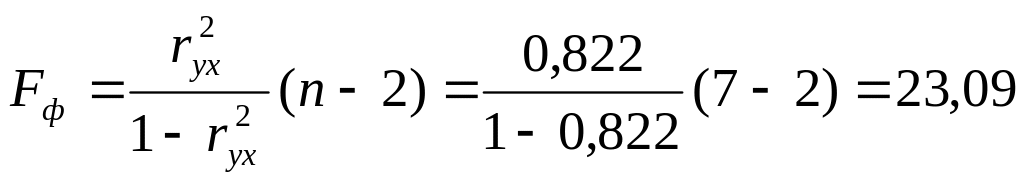
для α=0,05; k₁=m=1, k₂=n-m-1=5.

Уравнение регрессии с вероятностью 0,95 в целом статистически значимое, так как

Определим среднюю относительную ошибку:

В среднем расчетные значения для линейной модели отличаются от фактических значений на 5,68%.

Построение степенной модели парной регрессии.

Уравнение степенной модели имеет вид:

Для построения этой модели необходимо произвести линеаризацию переменных. Для этого произведем логарифмирование обеих частей уравнения: .

Обозначим Тогда уравнение примет вид: , то есть получили линейное уравнение регрессии. Рассчитаем его параметры, используя МНК.

Составим рабочую таблицу.

N	X	X	Y	Y	X2	XY
1	64	1,806	64	1.806	3,2623	3,2623	61,294	2,706	7,322	0,0423	180,36
2	68	1,833	56	1,748	3,3581	3,2036	58,066	-2,066	4,270	0,0369	29,485
3	82	1,914	52	1,716	3,6627	3,2841	49,133	2,867	8,220	0,0551	2,045
4	76	1,881	48	1,681	3,5375	3,1621	52,580	-4,580	20,976	0,0954	6,605
5	84	1,924	50	1,699	3,7029	3,2693	48,088	1,912	3,657	0,0382	0,325
6	96	1,982	46	1,663	3,9294	3,2960	42,686	3,314	10,982	0,0720	20,885
7	100	2,000	38	1,580	4,0000	3,1596	41,159	-3,159	9,980	0,0831	158
Сумма	570	13,340	354	11,893	25,4528	22,6370		0,51	65,407	0,4232	397,705
Среднее	81,43	1,906	50,57	1,699	3,6361	3,2339

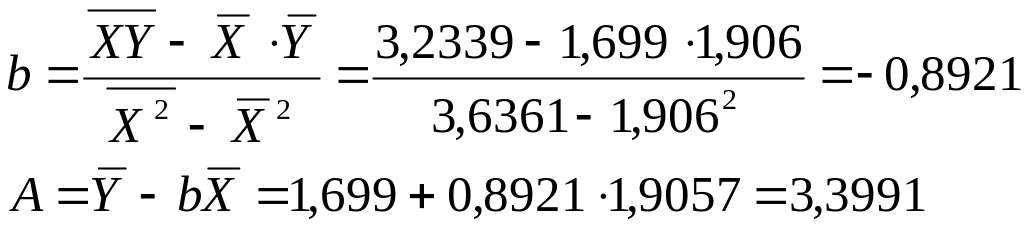
Уравнение регрессии имеет вид:

Перейдем к исходным переменным х и у, выполнив потенцирование данного уравнения.

Получим уравнение степенной модели регрессии

Так как в уравнении степенной регрессии параметр b совпадает с коэффициентом эластичности, то уравнение регрессии можно проинтерпретировать следующим образом: с увеличением объема капиталовложений на 1% объем выпускаемой продукции уменьшится в среднем на 0,892%.

Определим индекс корреляции

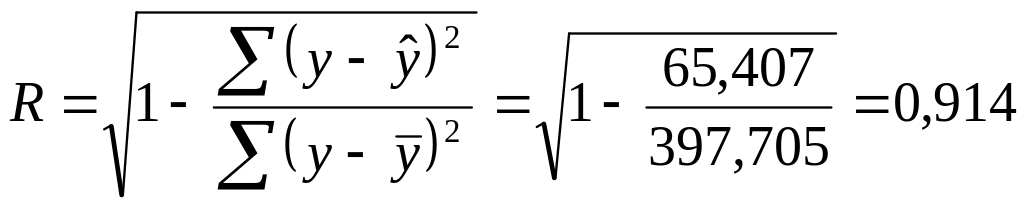
Связь между показателем у и фактором х можно считать достаточно сильной. Коэффициент детерминации

Вариация результативного признака у (объема выпуска продукции) на 83,6% объясняется вариацией фактора х (объемом капиталовложений).

Рассчитаем F-критерий Фишера:

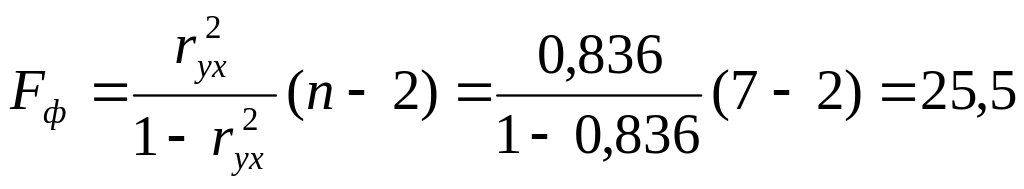
для α=0,05; k₁=m=1, k₂=n-m-1=5.

Уравнение регрессии с вероятностью 0,95 в целом статистически значимое, так как

Определим среднюю относительную ошибку:

В среднем расчетные значения для степенной модели отличаются от фактических значений на 6,04%.