2) Искажение высот точек

Если заменить небольшой участок сферы касательной плоскостью, то будут искажены не только длины линий, но и отметки точек. Изменения отметок симметричны относительно точки B и зависят от удаления от этой точки; обозначим отрезок BC', равный половине отрезка A'C', через s. Отметка точки C', находящейся на плоскости, отличается от отметки точки C, лежащей на сфере, на величину отрезка CC'=p (рис.1.7).

Из треугольника OBC' следует:

R² + s² = (R + p)²,

откуда получаем:

              (1.4)

В знаменателе величина p намного меньше величины 2∙R, поэтому, отбросив ее, мы допустим несущественную ошибку. Таким образом,

                 (1.5)

Влияние кривизны Земли на отметки точек нужно учитывать при любых расстояниях между точками; например, при s=10 км p=7.8 м и при s=100 м p=0.8 мм.

7. Системы координат, применяемые в геодезии

Система координат устанавливает начальные ( исходные) точки поверхности или линии отсчета необходимых величин – начало отсчета координат, единицы их измерения.

В геодезии и топографии получили применение системы географических, геодезических, пространственных прямоугольных, плоских прямоугольных и полярных координат.

1)Географические и геодезические координаты.

Географическими координатами являются угловые величины, называемые широтой и долготой, определяющие положение точки земной поверхности относительно экватора и начального меридиана.

Плоскость экватора проходит через центр Земли и перпендикулярна к её оси вращения;начальный меридиан- Гринвичский

Долгота- двугранный угол (λ) между плоскостью начального меридиана и плоскостью меридиана, проходящего через данную точку, измеряемый в экваториальной плоскости вправо и влево от начального меридиана, т.е. долгота бывает восточной (+) и западной (-) от 0 до 180˚

Широта-угол(φ) между радиусом шара, проходящим через данную точку , и плоскостью экватора. Широта на экваторе равно 0, на полюсах: северном +90˚на южном -90˚

2)Астрономические координаты

Астрономические- координаты, получаемые из непосредственных полевых наблюдений .

Положение точки на поверхности сферы определяется двумя сферическими координатами - широтой и долготой (рис.1.2: точка O - центр сферы, точка P - северный полюс, точка P' - южный полюс). Проведем линию экватора QQ, полученную от пересечения плоскости экватора и поверхности сферы.

Плоскость меридиана точки A, лежащей на поверхности сферы, проходит через отвесную линию точки A и ось вращения Земли PP'. Меридиан точки A - это линия пересечения плоскости меридиана точки A с поверхностью сферы.

Широта точки A - это угол, образованный отвесной линией точки A и плоскостью экватора; этот угол лежит в плоскости меридиана точки.

Широта отсчитывается в обе стороны от экватора (к северу - северная широта, к югу - южная) и изменяется от 0o до 90o.

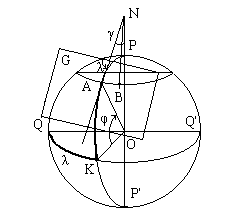
Рис.1.2

Долгота точки A - это двугранный угол между плоскостью начального меридиана и плоскостью меридиана точки A. Начальный меридиан проходит через центр главного зала Гринвичской обсерватории, расположенной вблизи Лондона. Долготы изменяются от 0⁰ до 180⁰, к западу от Гринвича - западные и к востоку - восточные. Все точки одного меридиана имеют одинаковую долготу.

Проведем через точку A плоскость, параллельную плоскости экватора; линия пересечения этой плоскости с поверхностью сферы называется параллелью точки; все точки параллели имеют одинаковую широту.

Проведем плоскость G, касательную к поверхности сферы в точке A; эта плоскость называется плоскостью горизонта точки A. Линия пересечения плоскости горизонта и плоскости меридиана точки называется полуденной линией; направление полуденной линии - с юга на север. Если провести полуденные линии двух точек, лежащих на одной параллели, то они пересекутся в точке на продолжении оси вращения Земли PP' и образуют угол , который называется сближением меридианов этих точек.

Широту и долготу точек местности определяют из астрономических наблюдений, потому они и называются астрономическими координатами.

В современной геодезии применяются такие системы координат как:

- эллипсоидальные( определяют положение тоски на поверхности эллипсоида)

-прямоугольные( двухмерные на плоскости, трёхмерные в пространстве).

К эллипсоидальным относятся геодезические координаты

Геодезические координаты

На поверхности эллипсоида вращения положение точки определяется геодезическими координатами - геодезической широтой и геодезической долготой

Геодезическая широта точки - это угол, образованный нормалью к поверхности эллипсоида в этой точке и плоскостью экватора.

Геодезическая долгота точки - это двугранный угол между плоскостью начального меридиана и плоскостью меридиана точки.

Геодезическую систему координат, связанную с общеземным эллипсоидом называют общеземной системой.

WGS-84(World Geodetic System,1984).Начало координат ее пространственной прямоугольной системы находится в центре масс Земли.

Из-за неравномерности размещения геодезических пунктов , погрешностей измерений, особенностей их математической обработки общеземные системы координат различаются между собой.

Геодезическую систему координат, связанную с референц-эллипсоидом, распространяемую в пределах материка или территории того или иного государства, называют референц-системой.

Геодезические системы координат включают:

-параметры эллипсоида

-высоту геоида над эллипсоидом в начальном пункте

-исходные геодезические данные( геодезическая широта и долгота начального пункта, азимут с начального пункта на ориентирный пункт геодезической сети).

Единая государственная система координат(СК-95).Принята при условии параллельности её осей пространственным осям системы координат ПЗ-90.Ха отсчетную поверхность принята поверхность референц-эллипсоида Красовского с его параметрами. Поверхность эллипсоида образуется в плоскую при помощи проекции Гаусса-Крюгера, сохранены неизменными координаты начального пункта Пулково.

Положение пунктов можно задавать следующими координатами:

• пространственными прямоугольными координатами X,Y,Z( направление оси Z совпадает с осью вращения отсчетного эллипсоида, ось X лежит в плоскости нулевого меридиана, а ось Y дополняет систему до правой; началом системы координат является центр отсчетного эллипсоида)

• геодезическими координатами: широтой, долготой, высотой. Геодезическая высота отсчитывается от точки на земной поверхности по нормали до поверхности эллипсоида.

• Плоскими прямоугольными координатами x и y , вычисляемыми в проекции Гаусса-Крюгера. Третья координата- абсолютная высота измеряется от среднего уровня Балтийского моря.

Геодезические координаты относятся к нормали к поверхности эллипсоида, а географические- к отвесной линии, т.е. нормали к уровенной поверхности, или к геоиду.

Уклонение отвесной линии - угол между отвесной линией и нормалью к поверхности эллипсоида.

Плоские прямоугольные координаты.

Особенность прямоугольных координат состоит в том, что они могут быть наложены на плоское изображения земной поверхности.