36 Определение координат точек методом засечек( стр 70)

Засечкой называется метод определения координат отдельной точки измерением элементов, связывающих ее положение с исходными пунктами.

Для определения планового положения точки необходимо измерить два элемента. Для контроля, кроме необходимых, выполняют избыточные измерения.

Засечки различают:

- прямые(измерения выполняют на исходных пунктах (рис. 6.6 a, г);

-обратные (на определяемом пункте (рис. 6.6 б, д);

- комбинированные(на исходных и определяемом пунктах (рис. 6.6 в)

В зависимости от вида измерений засечки бывают:

- угловые (рис. 6.6 a, б, в),

-линейные (рис. 6.6 г),

- линейно-угловые (рис. 6.6 д).

Измеренные углы на рис. 6.6 отмечены дугами, измеренные расстояния – двумя штрихами.

Рассмотрим вычисление координат в некоторых засечках.

Прямая угловая засечка. На исходных пунктах A и B с координатами ,  , ,  . (рис. 6.6 а) измеряют углы и . При обработке измерений сначала вычисляют дирекционные углы направлений AP и BP:

; .

Дирекционные углы с координатами связаны формулами обратной геодезической задачи

; .

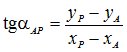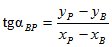Решая эти уравнения относительно x_p и y_p, получим формулы, по которым вычисляют координаты определяемой точки Р (формулы Гаусса):

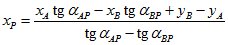; (6.5)

.

Для контроля ординату y_P вычисляют вторично по формуле:

.

 

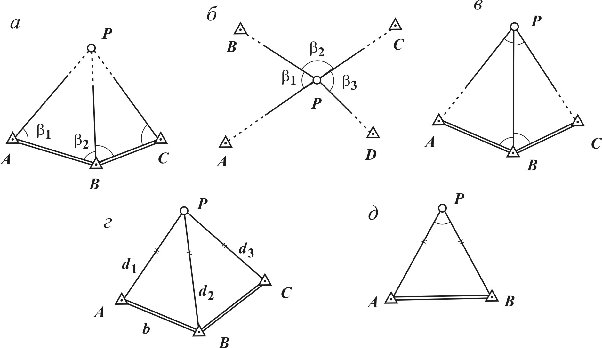
Рис. 6.6. Схемы засечек: а – прямая угловая; б – обратная угловая; в – комбинированная угловая; г – линейная; д – линейно-угловая

Если один из дирекционных углов или близок к или , то вместо формул (6.5 – 6.7) вычисления выполняют по формулам

;

.

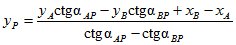Для контроля аналогичные измерения и вычисления выполняют, опираясь на другую исходную сторону BC. За окончательные значения координат определяемой точки принимают средние.

Существуют и иные формулы решения прямой угловой засечки, например, формулы котангенсов углов треугольника (формулы Юнга):

; .

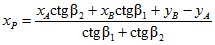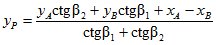Обратная угловая засечка. На определяемой точке P (рис. 6.6 б) измеряют углы и между направлениями на исходные пункты A, B и C. При этом исходные пункты выбирают такие, чтобы они с точкой P не оказались на одной окружности или вблизи нее. Координаты точки P вычисляют по формулам Гаусса (6.5 - 6.7), предварительно вычислив дирекционные углы:

; .

Для контроля измеряют избыточный угол и вычисляют координаты, используя другую пару измеренных углов.

Линейная засечка. Для определения координат точки Р (рис. 6.6 г) измеряют расстояния d₁, d₂. По формуле косинусов (6.1) находят углы треугольника АРВ. Вычисляют дирекционный угол a_АР = a_АВ - ÐA, а затем по формулам прямой геодезической задачи - искомые координаты

x_P = x_A + d₁cosa_АР; y_P = y_A + d₁sina_АР.

Для контроля измеряют избыточное расстояние d₃ и вычисляют координаты из другого треугольника ВРС.

37Теодолитный ход и его элементы

Задача прокладки теодолитного хода состоит в нахождении координат (x и y) ряда точек местности, закрепленных в натуре. Назначение работы может быть различным, в том числе создание геодезической основы для последующей топографической съемки.

Последовательность работ:

-разбивка полигона,

-измерение длин сторон и углов непосредственно в поле

- увязка углов теодолитного хода и нахождение линейной невязки

-подсчет невязки хода и относительной погрешности

- вычисление координат точек хода

-оформление результатов.

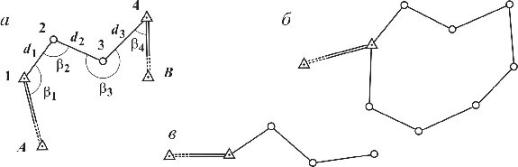
Рис. 6.5. Схемы теодолитных ходов: а – разомкнутого; б – замкнутого; в– висячего.

По форме теодолитный ход может быть разомкнутым - опирающимся на два исходных пункта и два исходных направления (рис. 6.5 а); замкнутым - опирающимся на один исходный пункт и одно направление (рис. 6.5 б); висячим - разомкнутым ходом, опирающимся на один исходный пункт и одно направление

Полевые работы начинают с разбивки полигона. На местности выбирают места для размещения точек хода, исходя как из возможности прокладки хода (видимости, отсутствия препятствий для измерения расстояний и пр.), так и учета дальнейшего использования пунктов, например для съемки местности. Все точки закрепляют колышками и отмечают «сторожками» во избежание потери. Над каждой точкой в очередности хода устанавливают прибор на

штативе. Теодолит нивелируют (ось вращения приводится в отвесное положение), центрируют (вертикальная ось совмещается с отвесной линией, проходящей через центр знака, фиксирующий в натуре вершину измеряемого угла) с точностью до 1 см. Затем прибор визируют по направлениям на вехи, установленные на точках (возможно ближе к земле во избежание ошибки в углах), производят отсчеты по лимбу и вычисляют углы. Одновременно с этим или раньше измеряют расстояния между точками хода. Длины сторон и углы измеряют дважды: линию — вперед и назад, угол — двумя приемами. Результаты должны расходиться не более чем 4 см на 100 м хода для длин

и на 1,5' — для углов.

Углы можно измерять либо правые, либо левые по ходу, но никак

не вперемежку. В замкнутом ходе удобно измерять внутренние углы

полигона

Угол левый получается по правилу: «отсчет вперед минус отсчет назад»: βлев = 3-1; угол правый — «отсчет назад минус отсчет вперед»: βпр = 1 - 3.

Особое внимание должно быть обращено на случаи, когда измеряемый угол близок к 180° и на глаз левый угол неотличим от правого.

Увязка углов теодолитного хода. 1. Для замкнутого хода не­

вязка получается по формуле , где n-число углов или сторон многоугольника. Допустимая погрешность:

(7.1)

где t — приборная точность измерения углов.

2. Для разомкнутого хода увязка начинается с вычисления обратной геодезической задачи и получения дирекционных углов твердых сторон (см. рис. 7.1, ). Затем производится передача дирекционных углов на все стороны хода:

или удобнее записать так:

Сложим все переходы от дирекционного угла первой «твердой» стороны до последней:

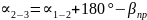
Запишем этот результат иначе:

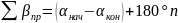
Теперь получим формулы для вычисления невязок в углах:

• для правых углов

• для левых углов

Поправка вводится во все углы поровну со знаком, противоположным знаку невязки.

Вычислим приращения координат по формулам

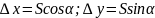(7.4)

Найдем линейную невязку теодолитного хода:

• для замкнутого хода

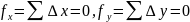(7.5)

• для разомкнутого хода

(7.6)

(7.7)

Если невязка не равна нулю, что практически получается всегда, то она с обратным знаком распределяется во все приращения координат пропорционально длинам сторон S

(7.8)

Абсолютная невязка теодолитного хода

(7.9)

Относительная невязка теодолитного хода

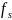/P = l/(P/ ) = l/N. (7.10)

Она задается в пределах от 1/1 ООО до 1/2000

Работа с теодолитным ходом завершается оформлением результатов: составляют каталог координат всех точек хода, по которым вычерчивают схему хода в масштабе с нанесенной сеткой. На схеме фиксируют все данные хода.