26Трилатерация

Изобретение электронных дальномеров позволило использовать

также метод линейной триангуляции — трилатерацию , когда вместо

углов в треугольниках измеряют длины всех сторон.

Трилатерация представляет собой сплошную сеть примыкающих один к другому треугольников, в которых измеряют длины всех сторон; два пункта, как минимум, должны иметь известные координаты (рис.2.25).

Решение первого треугольника трилатерации, в котором известны координаты двух пунктов и измерены две стороны, можно выполнить по формулам линейной засечки, причем нужно указывать справа или слева от опорной линии AB располагается пункт 1. Во втором треугольнике также оказываются известными координаты двух пунктов и длины двух сторон; его решение тоже выполняется по формулам линейной засечки и так далее.

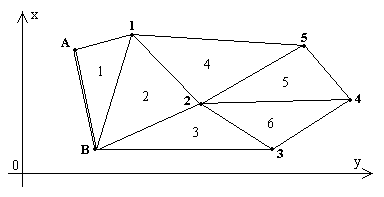
Рис.2.25. Схема сплошной сети трилатерации

Можно поступить и по-другому: сначала вычислить углы первого треугольника по теореме косинусов, затем, используя эти углы и дирекционный угол стороны AB, вычислить дирекционные углы сторон A₁ и B₁ и решить прямую геодезическую задачу от пункта A на пункт 1 и от пункта B на пункт 1.

Таким образом, в каждом отдельном треугольнике «чистой» трилатерации нет избыточных измерений и нет возможности выполнить контроль измерений, уравнивание и оценку точности; на практике кроме сторон треугольников приходится измерять некоторые дополнительные элементы и строить сеть так, чтобы в ней возникали геометрические условия.

Уравнивание сплошных сетей трилатерации выполняется на ЭВМ по программам, в которых реализованы алгоритмы МНК.

27Космическая геодезия. Задачи космической геодезии.

Космическая геодезия - раздел геодезии, в котором изучаются методы определения взаимного положения точек на земной поверхности, размеров и фигуры Земли, параметров ее гравитационного поля на основе наблюдений солнечных затмений и покрытий звезд Луной, а также наблюдений искусственных спутников Земли и аэростатов (баллонов) с импульсными источниками света, поднимаемых на высоту 20-30 км.

Космическая  геодезия рассматривает теорию и методы решения научных и практических задач на земной поверхности по наблюдениям небесных тел (Луна, Солнце, ИСЗ) и по наблюдениям Земли из космоса. 

Космическая геодезия включает в себя глобальные навигационные системы, являющиеся основой применяемых в настоящее время координатных систем, и системы космического дистанционного зондирования многоцелевого назначения, используемые для мониторинга поверхности Земли.

Задачи спутниковой геодезии подразделяются на геометрические и динамические.

Геометрические задачи решаются на основе одновременных (синхронных) наблюдений спутников с двух или более станций. В результате решения этих задач строятся сети космической триангуляции, подобные сейм триангуляции, создаваемым классическими (наземными) методами. Однако если в наземных сетях стороны треугольников обычно не превышают 20–30 км (расстояния между соседними геодезическими знаками — вышками), то в космической триангуляции они могут достигать нескольких тысяч километров.

В процессе решения динамических задач по изменениям орбит искусственных шутников исследуется строение гравитационного поля Земли, что позволяет также судить и о строении самой Земли.