22. Элементы взаимного расположения точек в плоской системе координат. Обратная геодезическая задача

См. 23.

Дано и ; и - координаты точке А и В.Следует найти угол положения и расстояние

tg

*Обратная геодезическая задача - это вычисление дирекционного угла α и длины S линии, соединяющей два пункта с известными координатами X₁, Y₁ и X₂, Y₂ (рис.2.5).

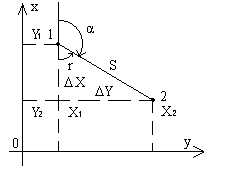
Рис.2.5

Построим на отрезке 1-2 как на гипотенузе прямоугольный треугольник с катетами, параллельными осям координат. В этом треугольнике гипотенуза равна S, катеты равны приращениям координат точек 1 и 2 (ΔX = X₂ - X₁, ΔY = Y₂ - Y₁), а один из острых углов равен румбу r линии 1-2.

Если Δ X ≠ 00 и Δ Y ≠ 00, то решаем треугольник по известным формулам:

              (2.9)

             (2.10)

Для данного рисунка направление линии 1-2 находится во второй четверти, поэтому на основании (1.22) находим:

               (2.11)

Общий порядок нахождения дирекционного угла линии 1-2 включает две операции:

определение номера четверти по знакам приращений координат Δ>X и ΔY (рис.1.4-а),

вычисление α по формулам связи (1.22) в соответствии с номером четверти.

Контролем правильности вычислений является выполнение равенства:

          (2.12)

Если ΔX = 0.0 , то

S = іΔY_і;

и α = 90^o 00' 00» при ΔY > 0 ,

α = 270^o 00' 00» при ΔY < 0 .

Если ΔY = 0.0 , то

S = іΔX_і

и α = 0^o 00' 00» при ΔX > 0 ,

α = 180^o 00' 00» при ΔX < 0 .

Для решения обратной задачи в автоматическом режиме (в программах для ЭВМ) используется другой алгоритм, не содержащий тангенса угла и исключающий возможное деление на ноль:

            (2.13)

если ΔY => 0^o , то α = a ,

если ΔН < 0^o , то α = 360^o – а.

23. Методы определения координат геодезических пунктов

Геодезический пункт - точка на земной поверхности, положение которой определено в известной системе координат и высот на основании геодезических измерений.

Координаты Г. п. определяют преимущественно методом триангуляции. В этом случае Г. п. называют пунктом триангуляции, или тригонометрическим пунктом.

Если координаты Г. п. определяются методом полигонометрии, то тогда он называется полигонометрическим пунктом. Высоты Г. п. определяют методом нивелирования. В общем случае пункты триангуляции и полигонометрии не совпадают с пунктами нивелирования. Пункты триангуляции, полигонометрни и нивелирные пункты обозначаются и закрепляются на местности путём возведения специальных сооружений. Система взаимно связанных Г. п. образует геодезическую сеть, которая служит основой топографического изучения земной поверхности и всевозможных геодезических измерений для различных нужд инженерного дела и народного хозяйства.

См. 24-28.

24. Триангуляция

Сущность метода триангуляции заключается в том, что на местности строится ряд примерно равносторонних треугольников,имеющих между собой последовательно одну смежную сторону. Ряд из нескольких треугольников образует звено, на концах которого определяют длины сторон.

Если измеряют непосредственно длины внешних сторон крайних треугольников, что бывает при малых длинах сторон, то эти стороны называют базисными или базисами. Если же из-за большой длины стороны определить ее невозможно, ее вычисляют опосредованно, строя так называемую базисную сеть, саму же сторону называют выходной.

Внутри треугольников измеряют углы необходимой точностью. Контроль и уравнивание углов производят из сравнения полученной суммы углов с теоретической, равной 180°.Начиная с выходной или базисной стороны, последовательно в каждом треугольнике длины двух других сторон определяют по теореме синусов:

BC=ABsinα/sinγ, AC=ABsinβ/sinγ

Перенесенная от стороны АВ к стороне базиса ее вычисленная длина сравнивается с результатом прямых или опосредованных измерений. Это позволяет ввести необходимые поправки и уравнять положение всех углов треугольников, составляющих сеть пунктов триангуляции, закрепленных в натуре более или менее капитально.

*Триангуляция представляет собой группу примыкающих один к другому треугольников, в которых измеряют все три угла; два или более пунктов имеют известные координаты, координаты остальных пунктов подлежат определению. Группа треугольников образует либо сплошную сеть, либо цепочку треугольников.

Координаты пунктов триангуляции как правило вычисляют на ЭВМ по программам, реализующим алгоритмы строгого уравнивания по МНК. На стадии предварительной обработки триангуляции последовательно решают треугольники один за другим. В нашем курсе геодезии мы рассмотрим решение лишь одного треугольника.

В первом треугольнике ABP (рис.2.24) известны координаты двух вершин (A и B) и его решение выполняют в следующем порядке:

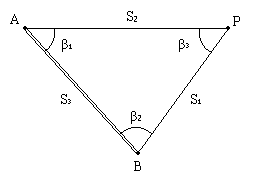
Рис.2.24. Единичный треугольник триангуляции

Вычисляют сумму измеренных углов ,

Принимая во внимание, что в треугольнике Σβ = 180о, вычисляют угловую невязку:

Поскольку

то        

Это уравнение содержит три неизвестных поправки β и решить его можно лишь при наличии двух дополнительных условий.

Эти условия имеют вид:

откуда следует, что

Вычисляют исправленные значения углов:

Решают обратную задачу между пунктами A и B вычисляют дирекционный угол αAB и длину S3 стороны AB.

По теореме синусов находят длины сторон AP и BP:

Вычисляют дирекционные углы сторон AP и BP:

Решают прямую геодезическую задачу из пункта A на пункт P и для контроля - из пункта B на пункт P; при этом оба решения должны совпасть.

В сплошных сетях триангуляции кроме углов в треугольниках измеряют длины отдельных сторон треугольников и дирекционные углы некоторых направлений; эти измерения выполняются с большей точностью и играют роль дополнительных исходных данных. При уравнивании сплошных сетей триангуляции в них могут возникнуть следующие условия:

условия фигуры,

условия суммы углов,

условия горизонта,

полюсные условия,

базисные условия,

условия дирекционных углов,

координатные условия.

Формула для подсчета количества условий в произвольной сети триангуляции имеет вид:

где n - общее количество измеренных углов в треугольниках,

k - число пунктов в сети,

g - количество избыточных исходных данных.