2.7. Задача поиска минимума квадратичной функции многих переменных.

MNT1R	безусловная минимизация методом M - покоординатного случайного поиска	89.2.12
MNP1R	минимизация при линейных ограничениях методом покоординатного спуска	89.3.10
MN11R	минимизация при двусторонних ограничениях на переменные методом покоординатного спуска	89.3.11

2.8. Задача поиска минимума функции многих переменных при наличии линейных ограничений общего вида.

MNR5R

метод условного градиента

89.3.9

2.9. Задача поиска минимума функции многих переменных при наличии ограничений общего вида.

MNI1R MNI1D	метод штрафных функций	89.3.3
MNBBR	метод скользящего допуска	89.3.12

3. Дерево выбора подпрограмм для решения задач целочисленного и линейного программирования.

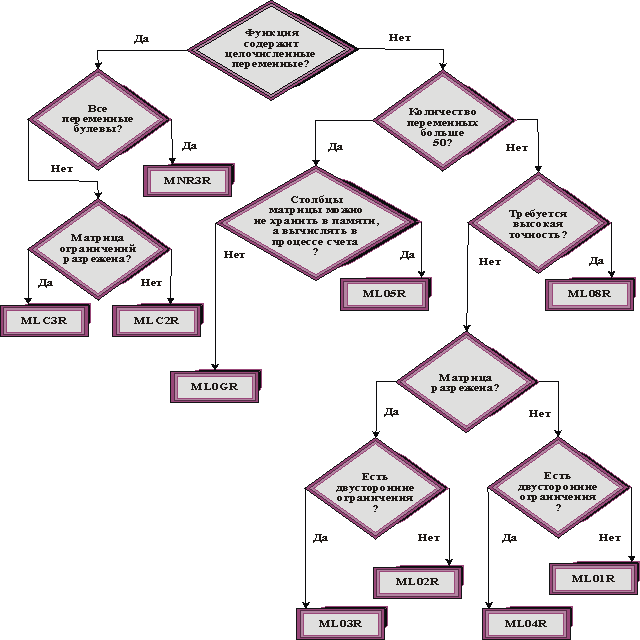
4. Дерево выбора подпрограмм для решения задач нелинейного программирования.

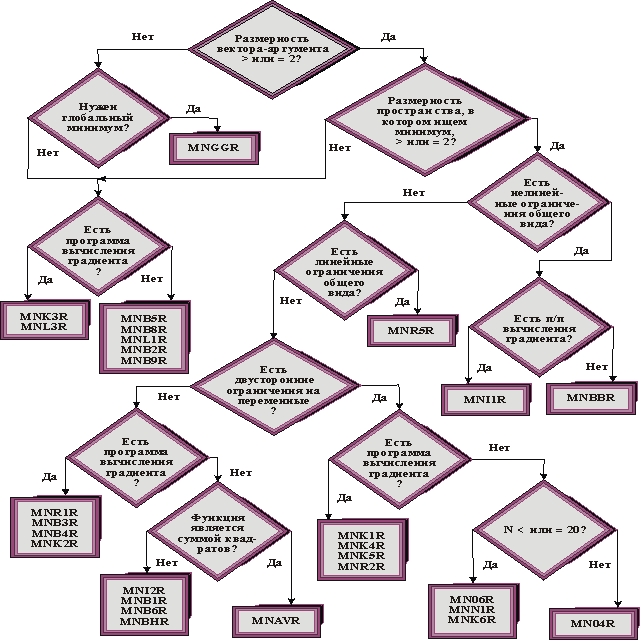
5. Подпрограммы, предназначенные для решения задач линейного программирования

При выборе той или иной подпрограммы симплекс - метода следует учитывать следующие факторы:

1.	размерность матрицы ограничений;
2.	количество ненулевых элементов в матрице ограничений;
3.	наличие двусторонних ограничений на переменные;
4.	требуемая точность вычислений.

Для задач не слишком большой размерности (количество ограничений не более 50, количество переменных не более 200, количество ненулевых элементов в матрице ограничений не более 5000) рекомендуется использовать подпрограммы ML01R, ML02R, ML03R, ML04R. При этом ML01R и ML04R предназначены для задач линейного программирования с большим (не менее 50%) количеством ненулевых элементов в матрице условий.

ML04R отличается от ML01R тем, что удобнее для задач, имеющих верхние ограничения на переменные. Подпрограммы ML02R и ML03R предполагают, что матрица условий сильно разрежена (более 50% нулевых элементов) и поэтому требуют компактного задания входной информации. ML03R в отличие от ML02R предполагает наличие верхних ограничений на переменные.

Подпрограмма ML05R вообще не требует хранения матрицы ограничений. Достаточно иметь подпрограмму, генерирующую столбец матрицы по его номеру. Подпрограмма ML08R решает задачу линейного программирования с повышенной точностью, т.к. на каждой итерации симплекс-метода базисная матрица преобразуется в произведение двух треугольных, после чего решаются две системы уравнений.

Подпрограмма MLOGR предназначена для решения больших задач линейного программирования (m  50, n  100) с разреженными матрицами условий. В ней используется мультипликативный вариант модифицированного симплекс - метода с пересчетами. Она, кроме того, алгоритмически учитывает верхние ограничения на переменные.