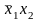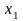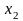Штрих Шеффера

Штрих Шеффера (отрицание конъюнкции, несовместимость, логическое НЕ-И). Эта функция названа по имени немецкого математика Шеффера, который на основе этой функции создал свою алгебру логики. Логико-математическая символика:

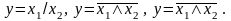Читается: x₁ и х₂ не.

Функцией штрих Шеффера называется функция которая ложна только тогда, когда x₁ и х₂ истинны.

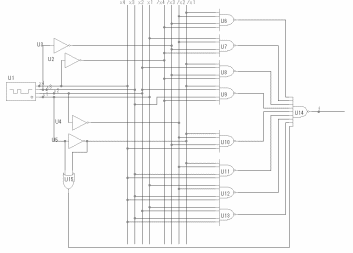
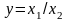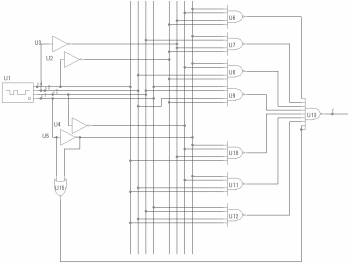
Для функции строится техническая реализация (см. рисунок 1.8) с помощью следующего соответствия .

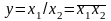(См. Приложение 4)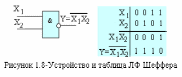

Штрих Шеффера (f1) =

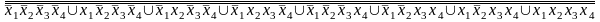
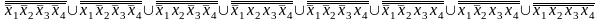
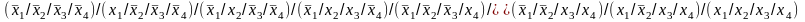
Штрих Шеффера (f2) =

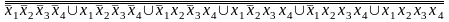
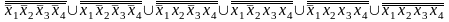
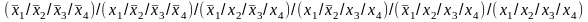
Штрих Шеффера (f3) =

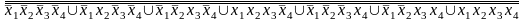
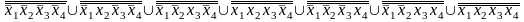
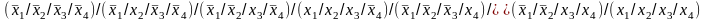
Штрих Шеффера (f4) =

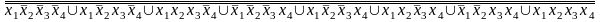
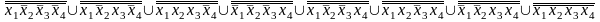
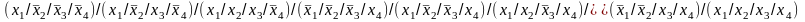
Методы минимизации функций алгебры логики Аналитический метод минимизации фл

Определение. Минимальная форма (МКФ и МДФ) представления ФЛ это форма, которая содержит минимальное количество термов и переменных в термах, и не должна допускать последующих упрощений.

Например, функция x₁+ x₂ может быть упрощена, если применить распределительный закон: x₁x₂+x₃=(x₁+x₃)(x₂+х₃), тогда

x₁+ x₂=( +x₁)(x₁+х₂)=x₁ +x₁x₁+ х₂+x₁x₂=

=0+x₁+х₂( +x₁)=x₁+х_2.

Упрощение сложных логических выражений может быть осуществлено на основании применения законов и аксиом алгебры логики, изложенных выше.

Пример. Пусть задана СДНФ

x₁x₂x₃+x₁x₂ +x₁ x₃+x₁ + x₂x₃=

(добавим еще один конъюнктивный терм x₁x₂x₃ согласно аксиомы х+х=х,) тогда,

=x₁x₂x₃+x₁ x₂ +x₁ x₃+x₁ +x₁x₂x₃+ x₂x₃=

(используем сочетательное и распределительное свойство конъюнкции и дизъюнкции)

=x₁x₂(x₃+ )+x₁ (x₃+ )+x₂x₃(x₁+ )=

=x₁x₂+x₁ +x₂x₃=x₁(x₂+ )+x₂x₃=x₁+x₂x₃.

В настоящее время существенные результаты в решении задач минимизации получены лишь для базиса НЕ, И, ИЛИ, т.к. этот базис наиболее распространен в технике проектирования ЦА. Именно этому базису мы будем уделять больше внимания в дальнейшем. С целью автоматизации процесса минимизации функций, на практике часто применяют числовое и геометрическое представление функций алгебры логики.

Метод квайна-мак-класки

При минимизации по методу Квайна предполагается, что минимизируемая функция представленна в СДНФ.

Метод Квайна состоит из последовательного выполнения нескольких этапов.

1-й этап. Нахождение первичных импликант.

Все минтермы данной функции сравниваются попарно. Если минтермы отличаются одной координатой типа Fх_i+F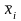 =F, то выписывается конъюнкция F, являющаяся минтермом (r+l)-гo ранга. Минтермы r-го ранга, для которых произошло склеивание, отмечаются.

Другими словами, нахождение простых импликант сводится к построению комплекса кубов

K(f) = К⁰ 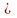К¹ К² … К^r.

При построении последующих кубов, образующие предыдущие кубы отмечаются, чтобы выявить неотмеченные кубы.

Этап заканчивается, когда ни один (r+1)-куб не может быть построен. При этом, все неотмеченные кубы комплекса K(f) тоже являются простыми импликантами и входят в покрытие C(f) функции f.

Пример. Пусть задана функция

F(х₁,х₂,х₃,х₄,х₅)= (0,1,2,3,4,5,14,15,16,17,18,19,21,23,31)

Для упрощения, 0-кубы упорядочивают по числу 1-ых координат (см. рисунок 8.1).

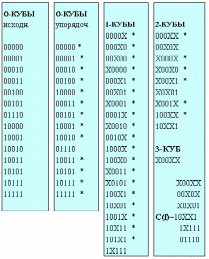
Простые и неотмеченные импликанты образуют покрытие С(f), которое может быть избыточным и требует последующих этапов минимизации, а именно - составления таблиц покрытия функции.

2-й этап. Составление таблиц покрытий.

Понятно, что для нахождения минимальной формы покрытия необходимо удалить из покрытия некоторые простые или неотмеченные импликанты. Для этого используют таблицу, строки которой составляют импликанты покрытия, а столбцы - 0-кубы (минтермы) исходной функции. Если импликанта отличается от 0-куба (кроме независимых координат), то на их пересечении не ставится метка + (см. таблицу 8.1).

Таблица 8.1-Таблица покрытий комплекса кубов

Импликанты	Вершины 0-кубов
	000000	000001	000010	000100	110000	000011	000101	110001	110010	001110	110011	110101	110111	111111
X00XX 00X0X X0X01 10XX1 1X111 01110	+ +	+ + +	+	+	+	+	+ +	+ + +	+	+ +	+ +	+ +	+ +	+

3-й этап. Определение существенных импликант.

Если в столбце таблицы покрытий имеется только одна метка, то первичная импликанта, стоящая в соответствующей строке, является существенной импликантой, и ее выписывают в новое минимальное покрытие C(f). Из таблицы покрытий исключаются строки, соответствующие существенным импликантам и столбцы минтермов, покрываемым этими существенными импликантами. Покрытие будет иметь вид :

C(f) = .

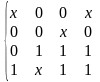
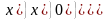В результате упрощения, получим новую таблицу 8.2

Таблица 8.2-Покрытия

импликанты	10101
X0X01 10XX1	+ +

4-й этап. Вычеркивание лишних столбцов.

Если в таблице существенных импликант есть два столбца имеющих метки в одинаковых строках, то один из столбцов вычеркивается.

5-й этап. Вычеркивание простых лишних импликант.

Если после вычеркивания столбцов в таблице появляются строки без меток, то импликанты этих строк вычеркиваются.

6-й этап. Выбор минимального покрытия.

В таблице, полученной после выделения существенных импликант, выбирается совокупность простых импликант, обеспечивающая покрытие всех столбцов с минимальной ценой С^A.

В нашем примере выбирается импликанта Х0Х01 ( или 10ХХ1, т.к. цены С^A одинаковы).

Таким образом, покрытие функции имеет вид:

С(f) =

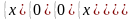
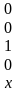
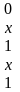
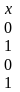
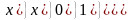
и определяет минимальную ДНФ

f = + 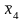+ x₂x₃x₄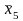 + x₅+x₁x₃x₄x₅.

При использовании метода Квайна для СКНФ необходимо рассматривать значения функций f=0 и макстермы, соответствующие этим значениям. В результате получим

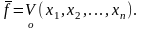
Далее необходимо воспользоваться соотношением де - Моргана с тем, чтобы привести функцию к СДНФ. Все дальнейшие действия аналогичны. (См. приложение 5)

МДНФ (f1)

0000
0001
0010
1000
0110
1100
1101
1111

000Х

00Х0

Х000

0Х10

1Х00

110Х

11Х1

	0000	0001	0010	1000	0110	1100	1101	1111
000Х	*	*
00Х0	*		*
Х000	*				*
0Х10			*	*
1Х00					*	*
110Х						*	*
11Х1							*	*

_МДНФ (f1)=

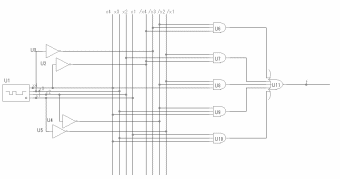
МДНФ(f2)

0000
0001
0010
1101
1110
1111

000X

00X0

11X1

111X

	0000	0001	0010	1101	1110	1111
000X	*	*
00X0	*		*
11X1				*		*
111X					*	*

МДНФ (f2)=

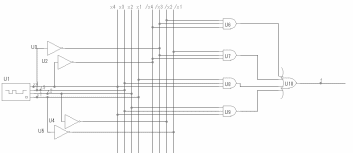
МДНФ(f3)

0000
0010
0100
1000
1100
0111
1111

00X0

XX00

X111

	0000	0010	0100	1000	1100	0111	1111
00X0	*	*
XX00	*		*		*	*
X111				*			*

_МДНФ(f3)=

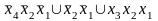
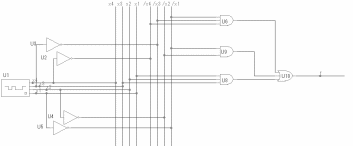
МДНФ(f4)

0001
1000
0101
1001
1100
0111
1011
1111

0X01

X001

100X

1X00

01X1

10X1

X111

1X11

	0000	0001	0010	1000	0110	1100	1101	1111
0X01	*	*
X001	*				*
100X				*	*
1X00				*			*
01X1		*	*
10X1					*	*
X111			*					*
1X11						*		*

_МДНФ (f4)=

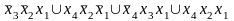
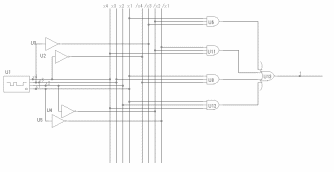
_{МКНФ (f1)}

0100
0011
0101
1001
1010
0111
1011
1110

010X

0X11

X011

01X1

10X1

101X

1X01

	0100	0011	0101	1001	1010	0111	1011	1110
010X		*	*
0X11	*			*
X011	*						*
01X1			*	*
10X1					*		*
101X						*	*
1X01						*		*

_МКНФ (f1)=

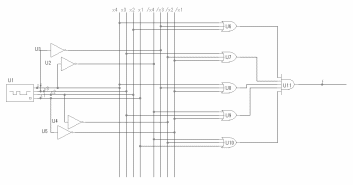
_{МКНФ (f2)}

0100
1000
0011
0101
0110
1001
1010
1100
0111
1011

01XX

X100

10XX

1X00

0X11

X001

	0100	1000	0011	0101	0110	1001	1010	1100	0111	1011
01XX		*	*	*	*
X100		*								*
10XX						*	*	*	*
1X00						*				*
0X11	*				*
X001	*								*

МКНФ (f2)=

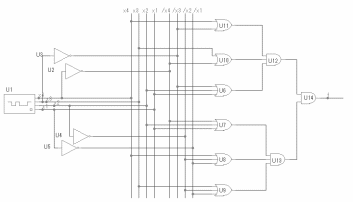
_{МКНФ (f3)}

0001
0011
0101
0110
1001
1010
1011
1101
1110

X0X1

XX01

X110

101X

1X10

	0001	0011	0101	0110	1001	1010	1011	1101	1110
X0X1	*	*			*		*
XX01	*		*		*			*
X110				*					*
101X						*	*
1X10						*			*

МКНФ (f3) =

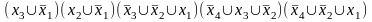
МКНФ (f4)

0000
0010
0100
0011
0110
1010
1101
1110

00X0

001X

XX10

X101

	0000	0010	0100	0011	0110	1010	1101	1110
00X0	*	*
001X		*		*
XX10		*			*	*		*
X101					*		*

МКНФ(f4)=

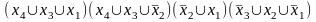
Метод Жегалкина

Метод Жегалкина или Сумма по модулю 2 (См. приложение 6)

Называется: сумма по модулю 2 (сложение по модулю 2, неравнозначность, анти эквивалентность).

Логико-математическая символика для двух переменных имеет несколько видов:

y = x₁ x₂, y = x₁ x₂,y =x₁+x₂, y =f(x₁, x₂,..., x_n)∙mod2.

Читается: сложение x₁ и х₂ по модулю 2.

Функцией сложения переменных по mod2 называется функция, которая ложна тогда, когда число истинных переменных четно или равно нулю и наоборот.

Очень часто применяется в технике цифровых автоматов для контроля правильности передачи информации по информационному каналу.

Для функции y=x₁ x₂ строится техническая реализация (см. рисунок 1.7) с помощью следующего соответствия:

x₁ x₂ = x₁ + x₂ = (x₁ + x₂)( + )

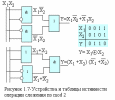
Метод Жегалкина (f1)=

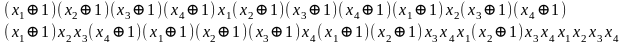
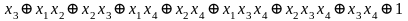
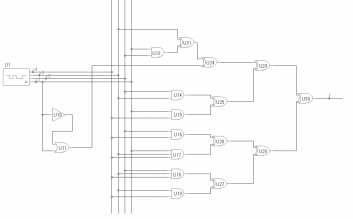
Метод Жегалкина (f2)=

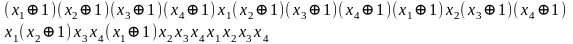
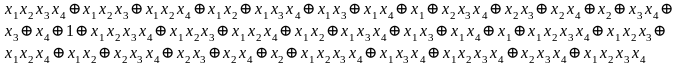
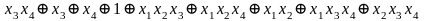
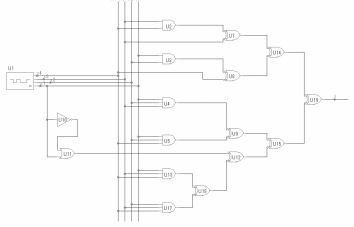
Метод Жегалкина (f3)=

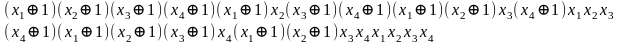
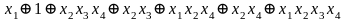
Метод Жегалкина (f4)=

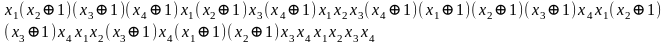
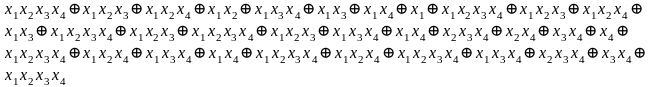
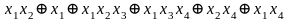
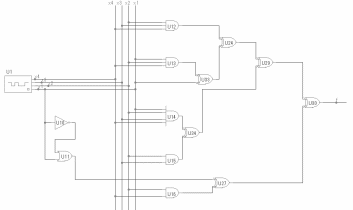
Вторая Часть

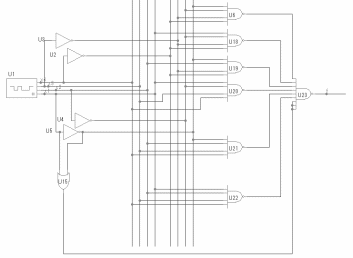
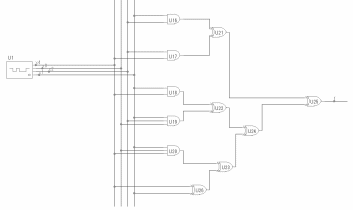
Во второй части курсовой работы необходимо выполнить синтез автомата по заданному алгоритму и построить его функциональную схему.

• Для получения исходного алгоритма управления необходимо соединить последовательно сверху вниз фрагменты блок-схемы алгоритма в порядке, указанном в таблице 1.

• В каждую логическую вершину полученной схемы, начиная с верхней переписать из таблицы 2 в указанном порядке по одной логической условию.

• Согласно таблице 3 записать в операторные вершины структурные управляющие сигналы.

• Выбрать тип триггеров из таблицы 4.

• Выбрать свой ​​вариант типа автомата.

h8	h4	h2	Порядок з'єднання фрагментів
0	0	1	2,4
h8	h7	h3	Логічні умови
0	1	0
h9	h4	h1	Послідовність управляючих сигналів
0	0	0	(y1 , y2 ), y3 , (y4 , y5 ), y2
h6	h5	Тригери	h4 = 0 - автомат Милли
1	1	T

Начало

y_1, y₂

X₁

0

y₃

X₂

1

y₂

y_4, y₅

0

Конец

Х₂ /y₂

Х₂/y₂

	Q1	Q2
Z1	0	0
Z2	0	1
Z3	1	0
Z4	1	1

ПС  СП	ПС			СП			Лог. Услов.		Управ. Сигналы							Функция возбуждения тригера
	Q1	Q2	Q1		Q2					У1	У2	У3	У4	У5	D1		D2
Z1 Z2	0	0	0		1	-		-		1	1	0	0	0	0		1
Z2  Z3	0	1	1		0	1		-		0	0	0	0	0	1		1
Z2  Z4	0	1	1		1	0		-		0	0	0	0	0	1		0
Z3  Z4	1	0	1		1	-		-		0	0	1	0	0	0		1
Z4  Z4	1	1	1		1	-		0		0	0	0	1	1	0		0
Z4  Z1	1	1	0		0	-		1		0	1	0	0	0	1		1

_У1 =

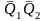
Q1\Q2	0	1
0	1	0
1	0	0

У₂ =

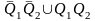
Q1\Q2	0	1
0	1	0
1	0	1

_У3=

Q1\Q2	0	1
0	0	0
1	1	0

_У4 =

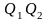
Q1\Q2	0	1
0	0	0
1	0	1

_У5=

Q1\Q2	0	1
0	0	0
1	0	1

D₁=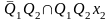

Q1 Q2\ Х1 Х2	00	01	11	10
00	0	1	0	0
01	0	1	1	0
11	0	1	1	0
10	0	1	0	0

_D1=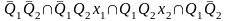

Q1 Q2\ Х1 Х2	00	01	11	10
00	1	0	0	1
01	1	0	1	1
11	1	1	1	1
10	1	1	0	1

Вывод В курсовой работе были синтезированы комбинационные схемы и построен функциональный управляющий автомат. Для этого в первой части была разработана переключающая функция, построены комбинационные схемы для базиса Буля, полинома Жегалкина, стрелки Пирса, штриха Шеффера, минимизированных функций базиса Буля. Кроме того, был синтезирован цифровой автомат, который отвечал условию во второй части курсовой работы. Для того, чтобы выполнить цель работы, были также рассмотрены некоторые разделы теоретических сведений по теории цифровых автоматов. Среди них: булевая алгебра, системы булевых функций, конъюнктивные и дизъюнктивные формы, полином Жегалкина, средства минимизации, абстрактные автоматы, триггеры. В первой части полученная таблица, которая состоит из состояний четырех функций, была представлена в разных формах базисов. Эти формы были преобразованы в комбинационные схемы в программе Micro Cap. По результатам синтеза можно сказать, что полученные формы из заданной таблицы правильны. Во второй части было составлено блок-схему, условия которой зависят от варианта, который составлен двоичным кодом зачетной книжки. По заданному типу автомата и полученной блок-схемы была составлена граф-схема, которая отвечает заданному автомату. По получению граф-схемы была составлена кодировка состояний автомата и таблицы, которая заключает в себе значения функций, переменных и триггеров, при переходе из одного состояния в другое. За таблицей были построены карты Карно для значений функций и триггеров. По картам Карно были построены логические выражения для триггеров и функций. Результаты работы находятся в самом тексте курсовой работы и в дополнениях.