Вопрос 2 Метод проекции

метод проекций: В пространстве выбирают произвольную точку S в качестве проецирования и плоскость П₁ не проходящую через точку S, в качестве плоскости проекций. Возьмем произвольную точку А. Через заданные точки S и А проводим прямую и отмечаем точку А₁, в которой эта прямая пересекает плоскость П₁.

.Различают 3 вида проецирования:

1) центральное - задают П - плоскость проекций и

S - центр проецирования. Для проецирования точки через нее и центр проецирования проводят прямую. Точка пересечения этой прямой с плоскостью проекций и является центральной проекцией заданной точки на выбранной плоскости проекций. Прямые, проходящие через центр проецирования и проецируемые точки, называют проецирующими прямыми. При ц.п. каждая точка пространства имеет только одну ц. пр-ю.

2) параллельное - можно рассматривать как частный случай центрального проецирования, при котором центр проецирования удален в бесконечность. При параллельном проецировании применяют параллельные проецирующие прямые и задается S - направление проецирования.

3) ортогональное -частный случай параллельного проецирования, при котором направление проецирования S перпендикулярно плоскости проекций. Ортогональной (прямоугольной) проекцией точки является основание перпендикуляра, проведенного из точки на плоскость проекций

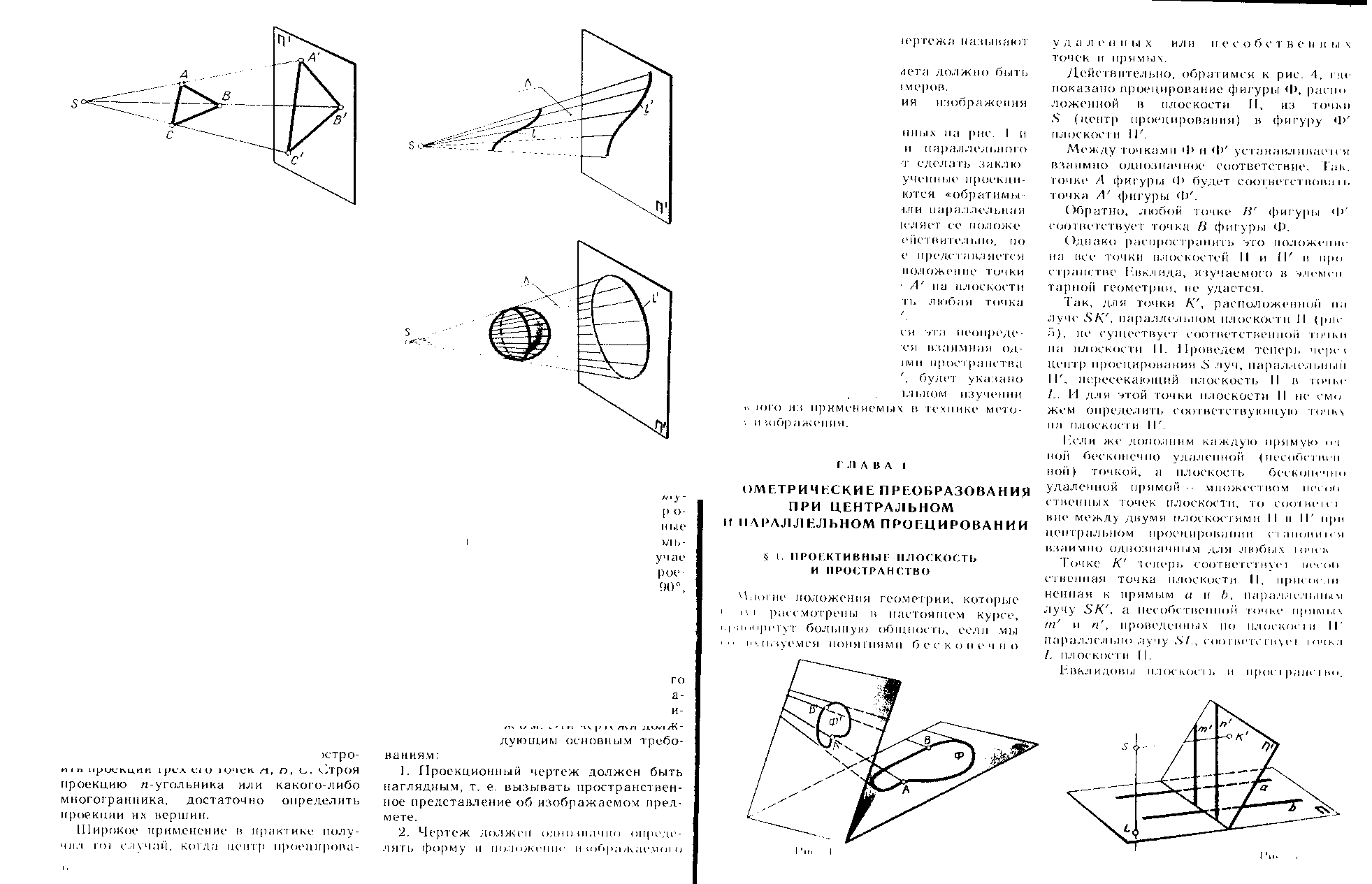
Вопрос 3 Эпюр Монжа. Проецирование точки на три плоскости

Положение точки на эпюре зависит от того в какой четверти находится данная точка. Плоскости проекций, попарно пересекаясь, определяют три оси: Ох, Оу и Оz, которые можно рассматривать как систему прямоугольных декартовых координат в пространстве с началом в точке О.

В качестве плоскостей выбирают три взаимно перпендикулярные плоскости. Три плоскости проекций делят пространство на восемь трехгранных углов – октантов

В результате получается чертеж, называемый эпюром Гаспара Монжа (1746-1818) – французского ученого, которым накапливавшиеся с древних времен приемы изображения пространственных форм на плоскости были приведены в систему и развиты в его трудах.

На эпюре две проекции одной и той же точки принадлежат прямой, перпендикулярной к оси проекций.

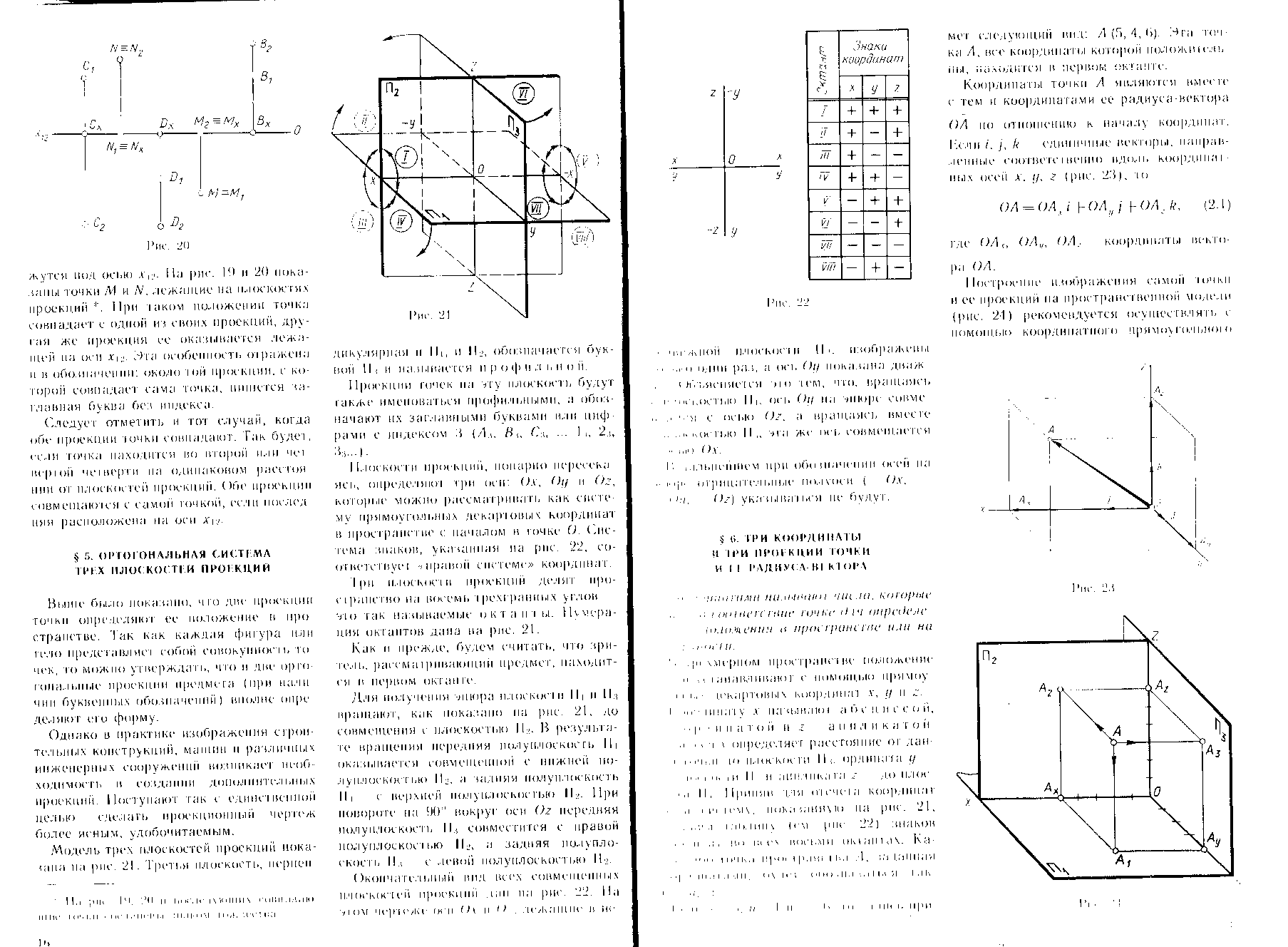
Рисунок 6

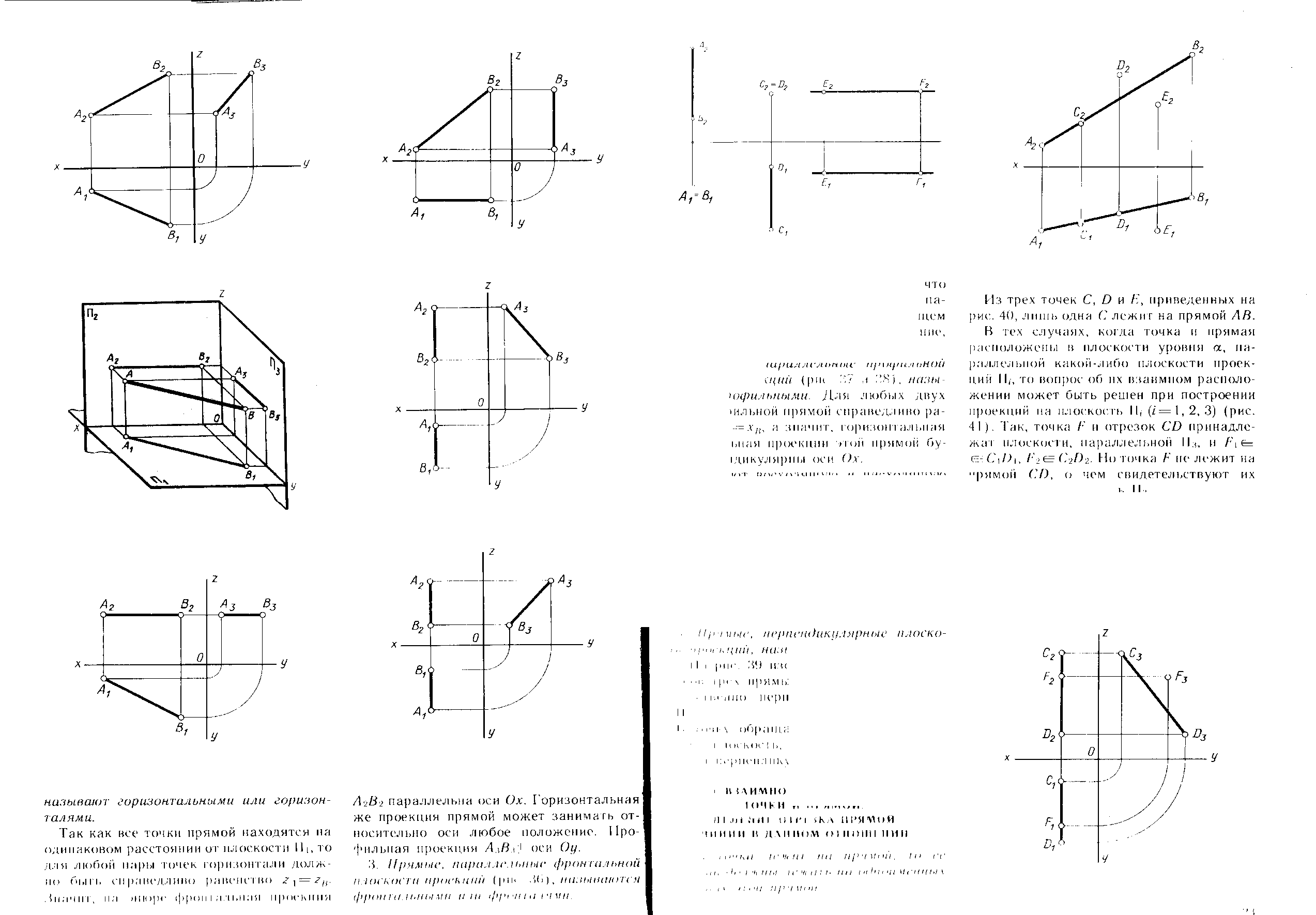
Вопрос 4 Взаимное положение точки и прямой

Если точка лежит на прямой, то ее проекции должны лежать на одноименных проекциях этой прямой Из трех точек С, D E лишь одна С принадлежит прямой АВ.

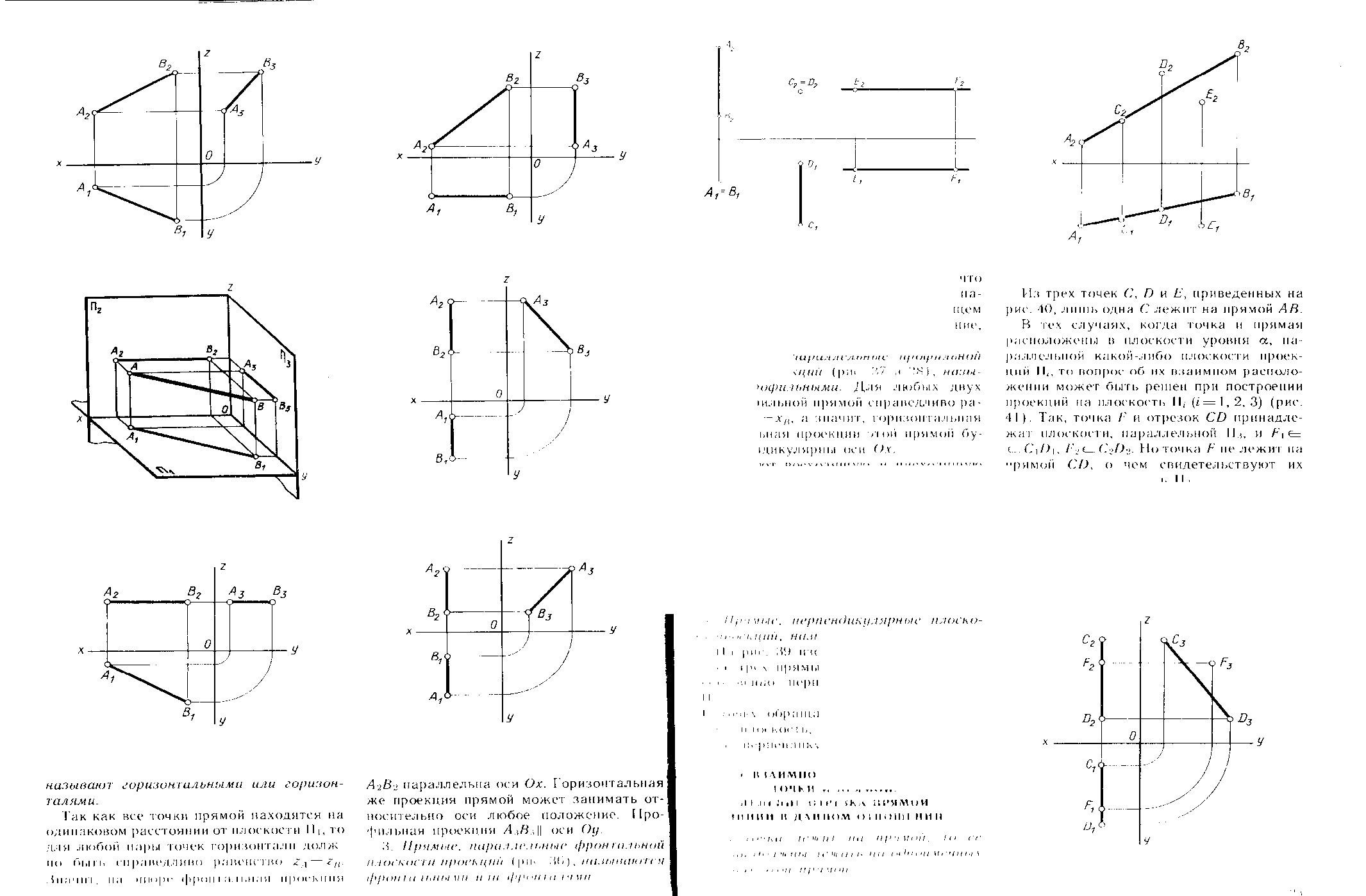
Рисунок 11

Деление отрезка прямой линии в данном отношении: Если точка лежит на прямой, то ее проекции должны лежать на одноименных проекциях этой прямой.

если точка делит отрезок прямой в данном отношении, то проекции этой точки делят одноименные проекции прямой в том же отношении.

Вопрос 5 Различные положения прямой относительно плоскостей проекций

прямой общего положения называется прямая не параллельная и не перпендикулярная ни одной из плоскостей проекций.

Прямые частного положения:

прямая, параллельная плоскости проекций;

прямая, перпендикулярная плоскости проекций.

Вопрос 6

Прямые, параллельные горизонтальной плоскости проекций называются горизонтальными или горизонталями

Вопрос 7

Прямые, параллельные фронтальной плоскости проекций называются фронтальными или фронталями

Вопрос 8

Прямые, параллельные профильной плоскости проекций называются профильными

Вопрос 9

1. Горизонтально проецирующая прямая - прямая горизонтальной плоскости проекций. Горизонтальной проекцией такой прямой является точка, а фронтальная и профильная проекции || оси z.

Вопрос 10 2. Фронтально проецирующая прямая - прямая фронтальной плоскости проекций. Фронтальной проекцией такой прямой является точка, а горизонтальная и профильная проекции || оси y.

Вопрос 11 3. Профильно проецирующая прямая - прямая профильной плоскости проекций. Профильной проекцией такой прямой является точка, а горизонтальная и фронтальная проекции || оси x.

Вопрос 12

Прямые, параллельные плоскостям проекций, называются прямыми уровня. Прямые, перпендикулярные плоскостям проекций, называются проецирующими.

Вопрос13

Прямые, параллельные горизонтальной плоскости проекций П₁ называются горизонтальными или горизонталями ( рисунок 24, а).

Вопрос 14

Прямые, параллельные фронтальной плоскости проекций П₂ называются фронтальными или фронталями (рисунок 24, б).

Прямые, параллельные профильной плоскости проекций П₃ называются профильными или профилями.

Вопрос 15 Взаимное положение прямых

Пересекающие прямые – прямые, а и b имеют одну общую точку, проекции которой Е₁ и Е₂ расположены на одной линии проекционной связи.

Если прямые пересекаются, то точки пересечения их одноименных проекций должны находиться на одной линии связи (рисунок 12).

Скрещивающиеся прямые – прямые, не имеющие общей точки. Если прямые не пересекаются и не параллельны между собой, то точки пересечения их одноименных проекций не лежат на одной линии проекционной связи (рисунок 13).

Параллельные прямые - если в пространстве прямые параллельны, то их одноименные проекции параллельны между собой (рисунок 14). Проекции параллельных прямых на любую плоскость параллельны.

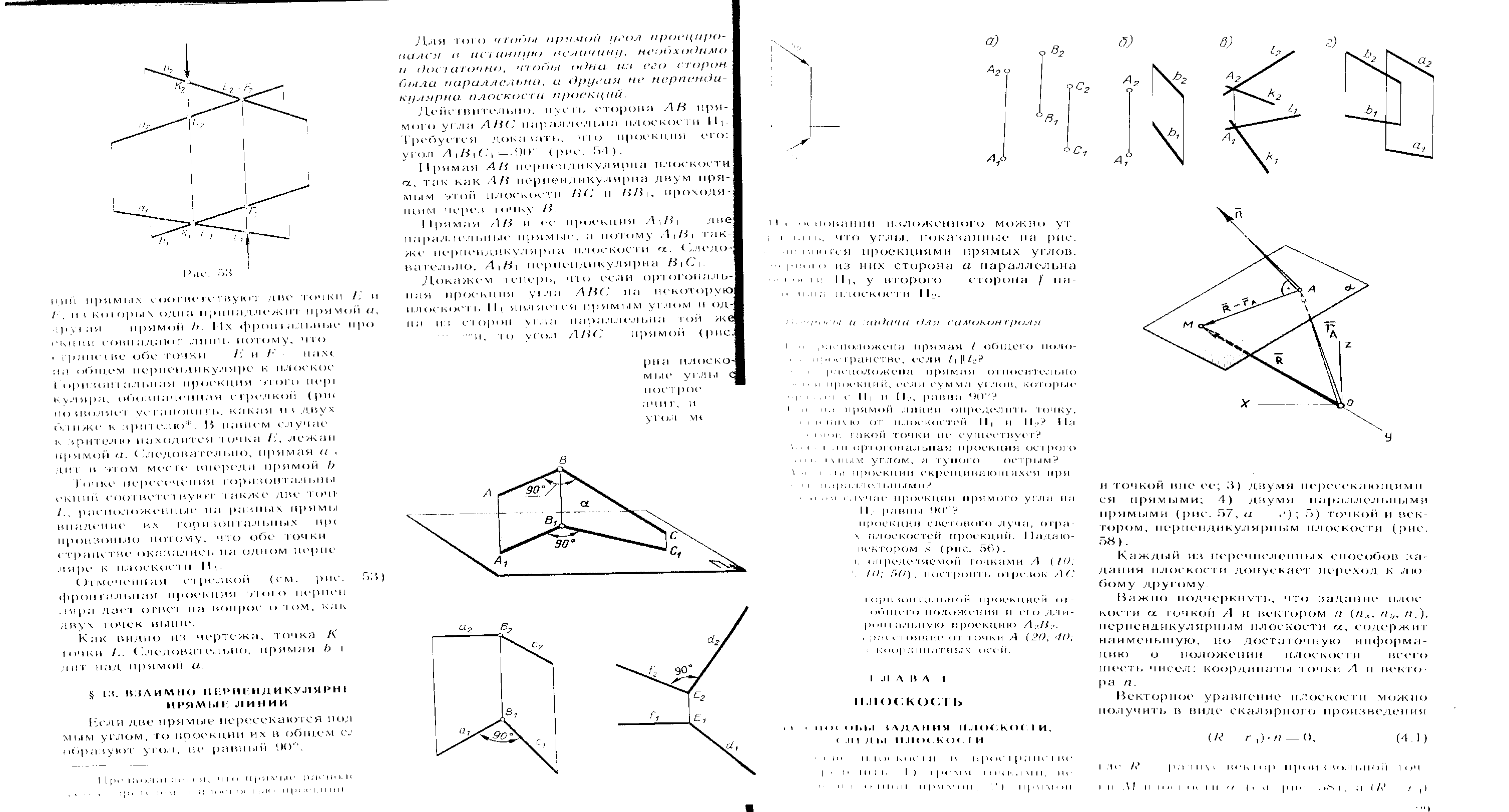
Рисунок 12 Рисунок 13 Рисунок 14