
- •Chapter I. Event and probability
- •1.Events. Operations above events.
- •2. Elements of combinatorics.
- •3. Classical definition of probability.
- •Properties of p(a)
- •4. Geometric definition of probability
- •Chapter II. Basic formulas
- •5. Conditional probability
- •6. Formula of total probability. Bayes’ formulas
- •Chapter III. Bernoulli scheme
- •7. Bernoulli’ formula
- •8. The most probable number of successes in n tests of Bernoulli
- •9. Approximated Poisson formula. Moivre-Laplace theorems
- •Chapter IV. Random variables
- •10. Definition of random variable. Function of distribution
- •11. Finite random variables
- •12. Continuous random variables
- •13. Examples of continuous random variables.
11. Finite random variables
Definition
11.1 A
random value
is called finite if the number of it’s values is finite. If these
values are:
![]() and
and
![]() ,
then can consider the table
,
then can consider the table
|
|
|
… |
|
|
|
|
… |
|
This table
we call the series of distribution of the random variable
.
![]() .
The set
.
The set
![]() we call the domain of the random variable
.
we call the domain of the random variable
.
If we have a
series of distribution we can construct the function of distribution.
If all
![]() are different and
are different and
![]() ,
then
,
then![]()
Definition
11.3 If
c
is
a constant, then the random variable
![]() is determined as follows:
is determined as follows:
|
|
|
… |
|
|
|
|
… |
|
Definition 11.4 The
random variable
![]() is called the
is called the
![]() degree of
and is determined by the following way:
degree of
and is determined by the following way:
|
|
|
… |
|
|
|
|
… |
|
Mathematical expectation of random variable
Let be a random variable with the series of distribution
|
|
|
… |
|
|
|
|
… |
|
Definition
11.8 Mathematical
expectation of
is the number![]() .
.
Properties
of
![]()
If c is a constant, then
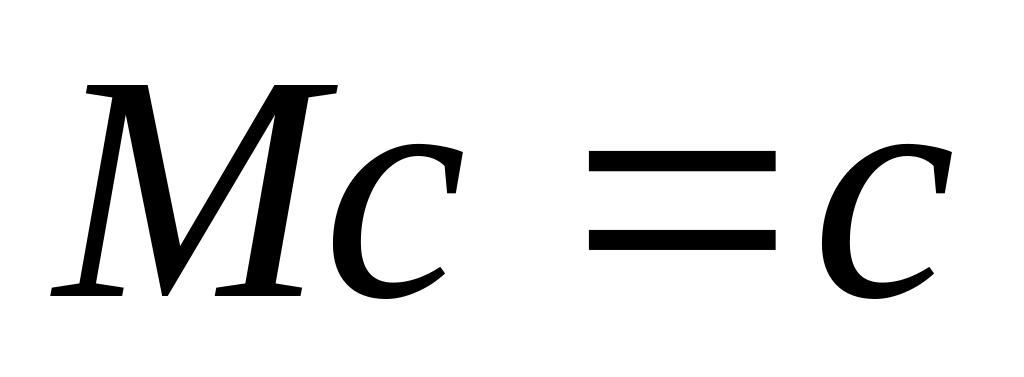 .
.If
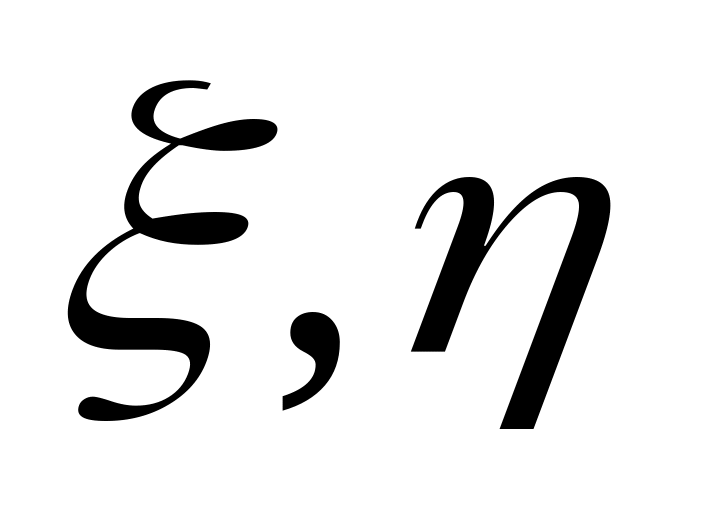 are random variables a,
b are
constants, then
are random variables a,
b are
constants, then
![]() .
.
If random variables are independent, then
![]() .
.
If
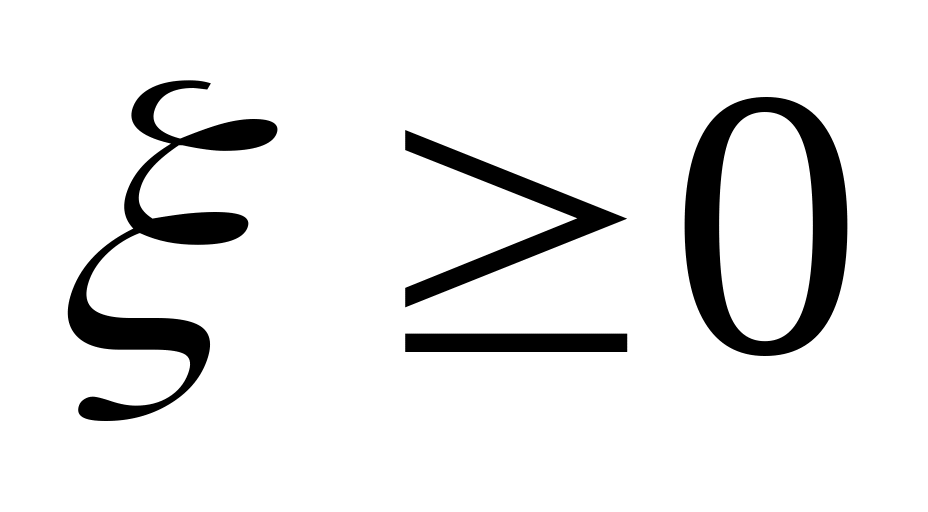 ,
then
,
then
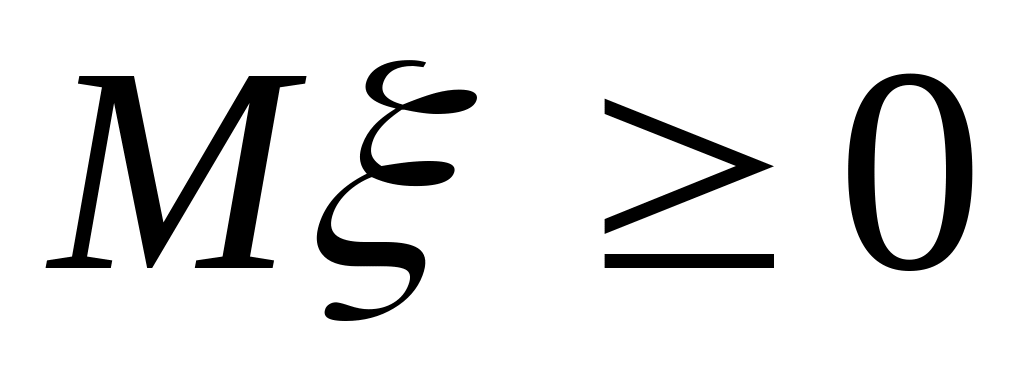 .
.If
 ,
then
,
then
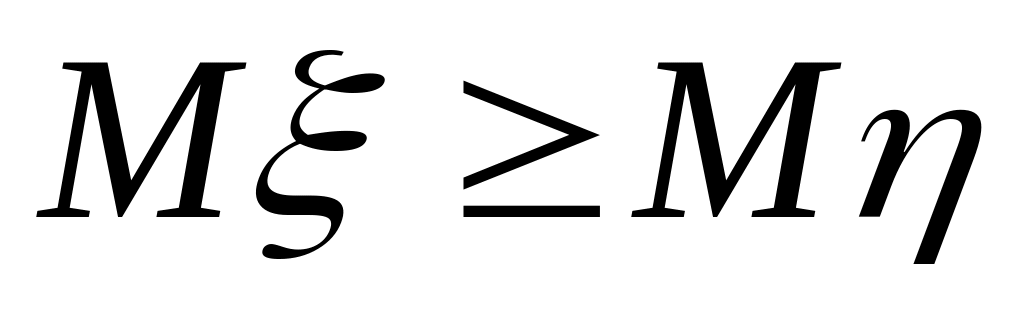 .
.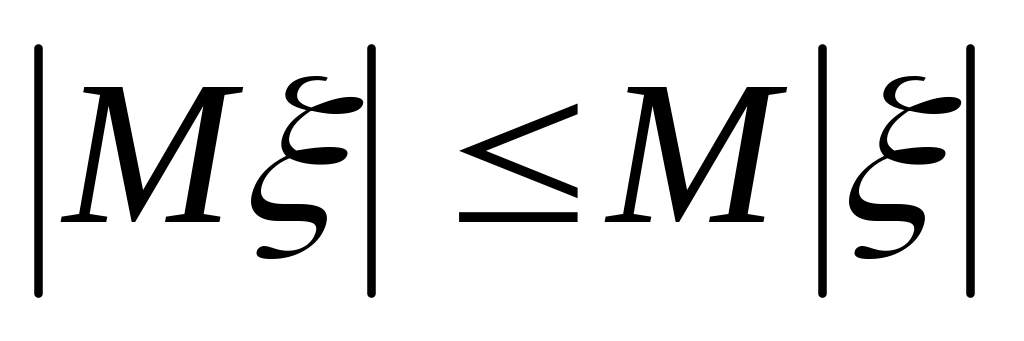 .
.
Dispersion of a random variable
Definition 11.10 A dispersion of a random variable is the number
![]() .
.
Remark 11.4
![]() .
.
Properties of dispersion
1.
![]() .
.
2. If c
is
a constant, then
![]() .
.
3. If c
is
a constant, then
![]() ..
..
4. If c
is
a constant, then
![]() .
.
5. If
and
![]() are
independent random variables
are
independent random variables![]()
Definition
11.11 The
number
![]() is called the standard deviation of
.
is called the standard deviation of
.
12. Continuous random variables
Definition
12.1 Let
be a random variable and
be the function of distribution of
.
Then
is continuous if there exists a function p![]() (x)
such that
(x)
such that![]() .
.
Definition 12.2 The function is called the integral function of distribution and p (x) is called the differential function of distribution or density of .
Properties of
1. .
2. If a domain of is (a, b), then
a)
![]() if
if
![]() ;
;
b)
increases if
![]() ;
;
c)
![]() if
if
![]() .
.
3.
![]() .
.
4.
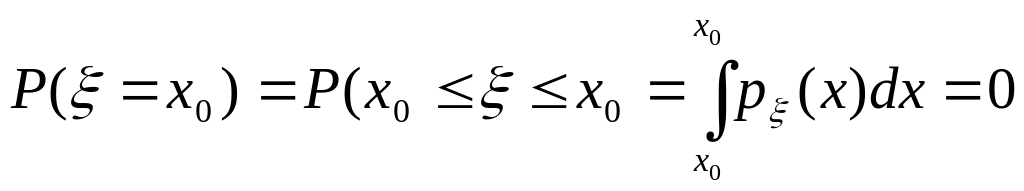 .
.
Properties of p (x)
1.
![]() .
.
2.
![]() .
.
![]() .
.
Characteristics of continuous variables
Definition
12.3 Let
be a continuous random variable with a domain
![]() .
Then
.
Then
a)
![]() ;
;
b)
![]()
c)
![]() .
.
13. Examples of continuous random variables.
1. Unitary law of distribution
Definition
12.4 The
law of distribution of a random variable
is called the unitary law if the differential function of
distribution
![]() is a constant for all values x
of it’s domain.
is a constant for all values x
of it’s domain.
Let
be a random variable with the unitary law of distribution with
nonzero values at the interval
.
Then
![]() for all
for all
![]() .
Our problem is to find C.
We
have
.
Our problem is to find C.
We
have
![]() .
.
So the differential function of distribution is
![]() .
.
2. Exponential law of distribution
Definition
12.5 The
law of distribution of a random variable
is called the exponential law with a parameter
![]() if the differential function of distribution
is:
if the differential function of distribution
is:
![]()
Then the integral function of distribution is
![]() .
.
Applying
integration by parts we obtain
![]()
![]() .
.
![]() .
.
![]() .
.
Theorem
12.1
![]() .
.
3. Normal law of distribution
Definition
12.6 The
law of distribution of a random variable
is called the normal law with parameters
![]() if the differential function of distribution
is:
if the differential function of distribution
is:
 .
.
Here we have the following formulas for characteristics of .
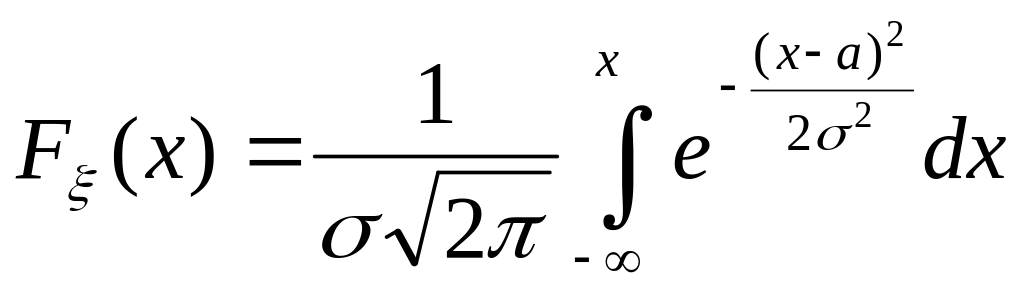 .
.
![]()
 .
.
![]()
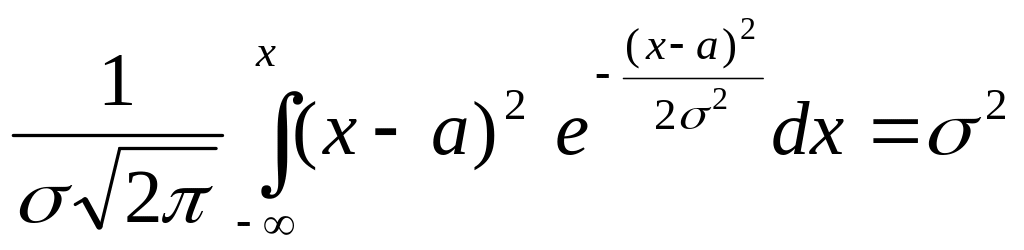 .
.
![]() .
.
Now we study
the function
![]() and sketch it’s graph.
and sketch it’s graph.
a). Domain:
![]() ;
;
b). Range:
![]() ;
;
c).![]() ;
;
d).
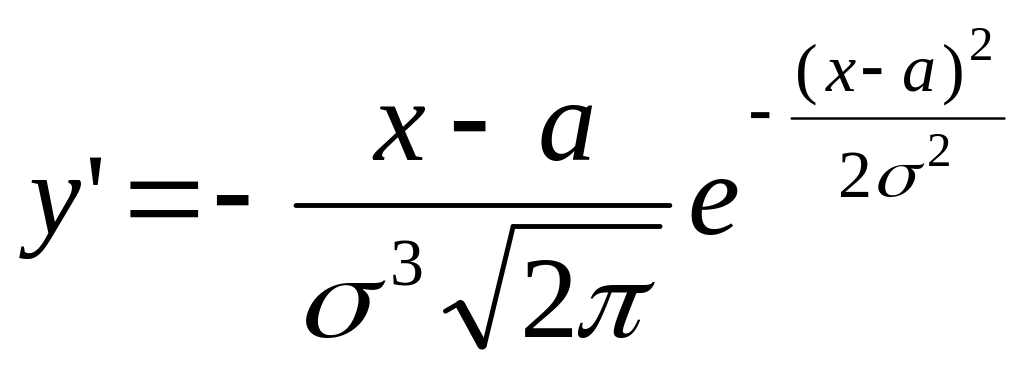 ,
so we have
,
so we have
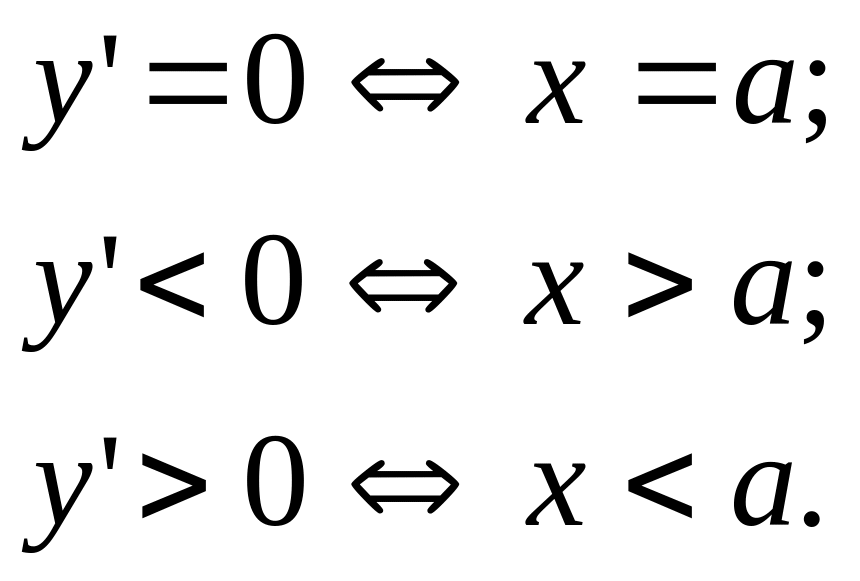
We obtain
that
![]() is the point of maxima,
is the point of maxima,
![]() .
.
e). If we
use the substitution
![]() ,
then we obtain
,
then we obtain
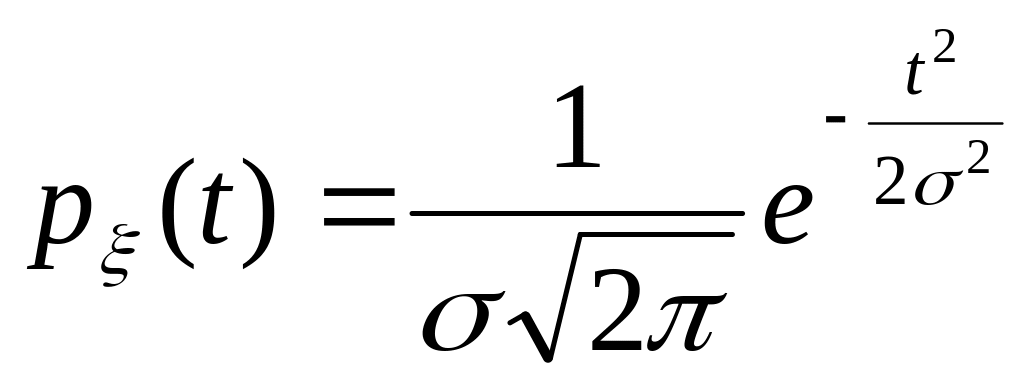 .
As
.
As
![]() is the even function then the graph of
is symmetric around the line x
= a.
is the even function then the graph of
is symmetric around the line x
= a.
Theorem 12.2 Let be the normal variable with parameters . Then
![]()
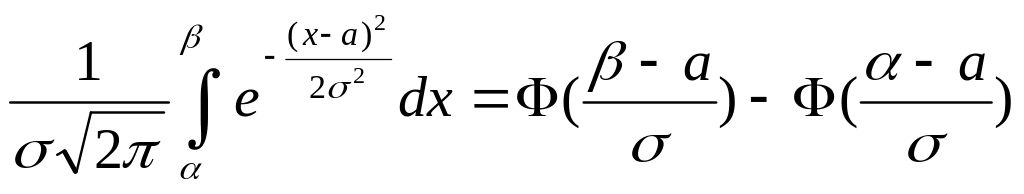 .
.
